
Лекция 11.
Разностные схемы для уравнений с частными производными.
Итак, мы приступаем к обсуждению методов численного решения задач для уравнений в частных производных. Источником таких задач большей частью является математическое моделирование физических процессов. Поэтому раздел математики, связанный с изучением свойств решений уравнений в частных производных, называется математической физикой (а сами уравнения - уравнениями математической физики).
Это очень развитая и сложная часть численных методов. В рамках нашего курса стоит цель - получить пусть первоначальные, но достаточно строгие представления о способах построения разностных схем для решения задач математической физики.
Рассмотрим следующие модельные уравнения:
∂u |
+ a |
∂u = f (x,t) |
- уравнение переноса |
|
∂t |
|
∂x |
|
|
∂u |
= k |
∂2u |
(k > 0) |
- уравнение теплопроводности (или диффузии) |
∂t |
|
∂x2 |
|
|
∂2u + ∂2u = − f (x, y) - уравнение Пуассона.
∂x2 ∂y2
Первые два уравнения описывают эволюцию состояния u(x,t) во времени t и пространстве x . Эти уравнения называют эволюционными или нестационарными. Третье уравнение описывает установившееся (стационарное) состояние функции u(x, y) в пространстве (x, y).
Классификация уравнений с частными производными второго порядка.
Общий вид уравнения: F (x, y,u,ux ,uy ,uxx ,uyy )= 0 .
Уравнение называется линейным, если оно линейно как относительно старших производных, так и относительно функции u и ее первых производных ux и uy .
Общий вид линейного уравнения второго порядка:
98

a11uxx + 2a12uxy + a22uyy +b1ux +b2uy + c u + f = 0 , где коэффициенты a,b,c и
функция f зависят только от x и y .
Линейное уравнение называется линейным уравнением с постоянными
коэффициентами, |
если a11,a12 ,a22 ,b1,b2 ,c = const . В этом случае заменой пере- |
||
менных можно привести к каноническому виду: |
|||
uξξ +uηη +b1uξ +b2uη +cu + f = 0 |
- уравнение эллиптического типа. |
||
uξξ −uηη +b1uξ +b2uη + cu + f = 0 |
- уравнение гиперболического типа. |
||
uξξ +b1uξ +b2uη + cu + f |
= 0 |
- уравнение параболического типа. |
|
ξ = ξ(x, y), |
η= η(x, y). |
|
|
Уравнение переноса является гиперболическим уравнением в частных производных первого порядка. В зависимости от классификации, уравнения в частных производных обладают специфическими свойствами, о главных из которых будет рассказано ниже.
1. Рассмотрим модельное уравнение конвективного переноса
∂u |
+ a(x,t) |
∂u |
= f (x,t) |
(1) |
∂t |
|
∂x |
|
|
Левая часть этого уравнения представляет собой полную производную по
t от функции u(x,t) в направлении с угловым коэффициентом dxdt = a(x,t): dudt = ∂∂ut + ∂∂ux dxdt = ∂∂ut + a(x,t) ∂∂ux .
Поэтому уравнение (1) может быть записано в характеристической форме
du |
= f (x,t), |
dx |
= a(x,t) |
(2), (3) |
|
dt |
dt |
||||
|
|
|
Уравнение (1) является математической моделью процесса одномерного переноса тепла (или вещества) средой, движущейся со скоростью a(x,t) при отсутствии теплопроводности (или диффузии, соответственно) с учетом возможных источников или стоков, интенсивность которых задается функцией f (x,t).
Важную роль в исследовании уравнения (1) играют характеристики – интегральные кривые ОДУ (2), (3). Характеристики являются линиями тока: ха-
99
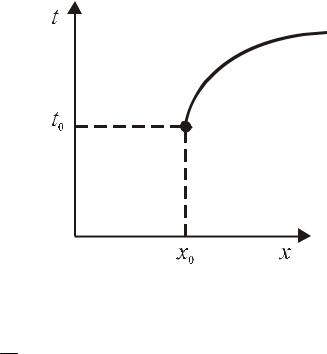
рактеристика x = x(t,t0 , x0 ) отображает на плоскости (x,t) движение частицы не-
сущей среды (Рис.11.1), имеющей в момент времени t = t0 координату x = x0 .
Рис. 11.1 Характеристика уравнения переноса
Уравнение dudt = f (x,t) на фиксированной характеристике является ОДУ с искомой функцией u , начальным условием u = u0 при t = t0 .
В случае чистого переноса, f (x,t)= 0 , имеем на характеристике u = const .
При a = const уравнение сразу интегрируется: x − at = C = const . В этом случае характеристики являются семейством параллельных прямых.
2.Краевые задачи для ограниченной области. Пусть G есть прямоугольник {0 ≤ t ≤T , 0 ≤ x ≤ X }.
При t = 0 задается начальное условие u(0, x)= (x). Кроме того, теперь еще нужно описать перенос тепла (массы) из внешней среды на отрезок [0, X ]. Это означает, что u(x,t) следует задавать в тех точках граничных линий x = 0 и x = X , где характеристики входят в область G .
Так, при a > 0 u(x,t) задается слева, т.е. при
100
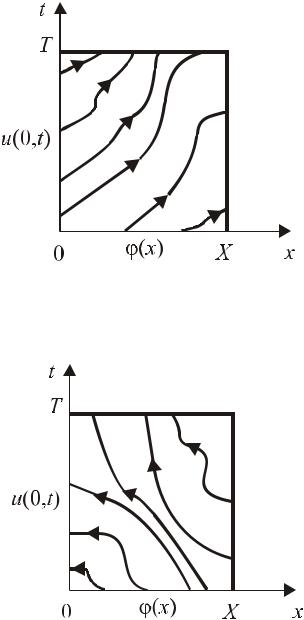
Рис. 11.2а Направление характеристик при a > 0
При a < 0 u(x,t) задается справа, т.е. при x = X , Рис. 11.2б.
Рис. 11.2б Направление характеристик при a < 0
Нетрудно указать корректные постановки задач и для более сложных случаев расположения характеристик.
3. Рассмотрим однородное уравнение переноса.
∂u |
+ |
∂u |
= 0 , т.е. a =1, f = 0 . |
(4) |
∂t |
|
∂x |
|
|
Для формирования разностной схемы, соответствующей этому ДУ, выберем шаблон “явный левый уголок” (Рис. 11.3):
101
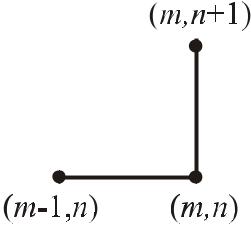
Рис. 11.3 Шаблон “явный левый уголок”.
На этом шаблоне разностная схема будет иметь следующий вид
|
un+1 −un |
un −un |
= 0 . |
(5) |
||
|
m |
m |
+ |
m m−1 |
||
|
|
|
h |
|||
|
|
τ |
|
|
||
Эта разностное уравнение аппроксимирует ДУ (4) в узле (m, n) |
с первым |
|||||
порядком точности. Это означает, что если в уравнении (5) все функции разложить в ряд Тейлора в точке (m, n), то получится уравнение (4) плюс выраже-
ние вида Ο(h + τ).
Упражнение. Выполнить разложение в ряд Тейлора и показать первый порядок аппроксимации ДУ (4) РС (5).
Для того, чтобы решение РС (5) сходилось к решению ДУ (4), РС должна не только аппроксимировать ДУ (4), но и быть устойчивой. Провести обоснование устойчивости схем для тех уравнений, которые встречаются в современных прикладных исследованиях, как правило, не удается. Тем не менее, необходимость в таких обоснованиях существует.
Для исследования на устойчивость разностных схем, аппроксимирующих эволюционные задачи, разработаны некоторые практические приемы, позволяющие относительно легко отсеивать неустойчивые схемы. Эти приемы проверены многочисленными опытами практических расчетов и обоснованы теоретически для некоторых достаточно общих модельных задач. Важное место среди них занимает метод гармонических возмущений (метод Фурье).
102
Метод гармонических возмущений (метод Фурье).
Задача Коши для линейного однородного ДУ, например, уравнения (4), имеет решения u(x,t)= exp(μt)exp(iωx), где ω- произвольное вещественное число.
(6)
Подставляя u(x,t) из (6) в уравнение (4), получим μ = −iω
теплопроводности |
∂u |
= k |
∂2u |
(k > 0) получим μ = −ω2 ). |
|
∂t |
|
∂x2 |
|
Оказывается, что решения вида (6) имеют также линейные однородные сеточные уравнения с постоянными коэффициентами.
На сетке tn = nτ, xm = mh введем функцию umn = λn exp(iωmh) , где λ = exp(μt). (7)
Подставляя выражение для umn в разностное уравнение с шаблоном “явный левый уголок” (5), получим
|
|
|
λn+1 exp(iωmh)−λn exp(iωmh) |
+ |
λn exp(iωmh)− λn exp(iω(m −1)h) |
= 0 |
||||||
|
|
|
|
|
|
|
h |
|
||||
|
|
|
|
τ |
|
|
|
|
|
|||
|
Отсюда получим |
λ−1 |
+ |
1−exp(−iωh) |
= 0 , или λ = (1− k )+ k exp(−iωh), где |
|||||||
|
τ |
|
|
|||||||||
|
|
|
|
|
h |
|
|
|
|
|||
k = |
τ |
> 0 . |
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Решения вида (7) можно рассматривать как возмущение, вызванное соответствующим возмущением начальной функции. Ограниченность этих возмущений при h →0 принимается в качестве главного практического критерия устойчивости схемы.
Прежде чем применять этот критерий, сеточное уравнение, аппроксимирующее ДУ, линеаризуется. Переменные коэффициенты “замораживаются”. Краевая задача заменяется соответствующей задачей Коши и анализируется влияние гармоники.
4. Условие Неймана.
Необходимое и достаточное условие ограниченности гармонических
возмущений имеет следующий вид: |
|
λ |
|
≤1+ cτ, |
c = const . |
(8) |
|
|
|||||
Действительно, пусть выполнено условие (8). Тогда при t = nτ≤T |
имеем: |
|||||
103
λn ≤ (1+ cτ)Tτ ≤ exp(cT ). Достаточность условия (8) доказана.
Докажем необходимость. |
|
|
|
|
|
|
|
|||||||
Пусть при t ≠ nτ≤T |
для некоторого L >1 имеем |
|
λn |
|
≤1. Полагая nτ =T , на- |
|||||||||
|
|
|||||||||||||
ходим |
1 |
|
|
L |
. Положим D = |
(ln L) |
. Рассматривая график функции |
|||||||
|
|
|||||||||||||
λ |
< Ln = exp |
τ ln |
|
|
|
|
||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
||||
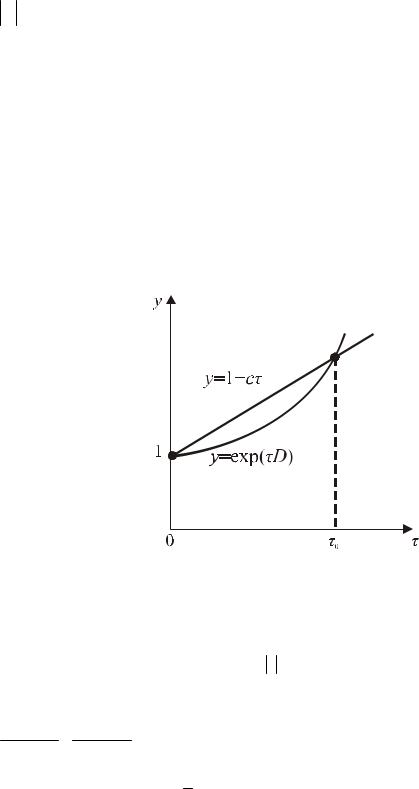
y = exp(τD) на отрезке 0 ≤ τ≤ τ0 , где τ0 - произвольное фиксированное положи-
тельное число (Рис. 11.4), убеждаемся в существовании постоянной c такой, что exp(τD)≤1+ cτ , т.е. условие (8) выполнено.
Рис. 11.4 График функции y = exp(τD)
В дальнейших оценках будем пользоваться более строгим, достаточным условием ограниченности возмущений λ ≤1 .
Возвращаясь к РС с шаблоном “явный левый уголок”,
un+1 −un un −un
+m m 1 = 0 ,
τh
λ= (1− k )+ k exp(−iωh), k = hτ > 0 .m m −
На комплексной плоскости точка, соответствующая λ, пробегает при изменении ω окружность радиуса k с центром в точке λ =1−k (Рис. 11.5).
104

Рис. 11.5 Геометрическое место точек λ.
Отсюда следует, что схема «явный левый уголок» устойчива при k ≤1 , т.е. при τ ≤ h и неустойчива при k >1, т.е. при τ > h . Таким образом эта РС условно устойчива.
5. Рассмотрим РС с шаблоном “явный правый уголок”( Рис. 11.6)
Рис. 11.6 Шаблон “явный правый уголок”
На этом шаблоне разностная схема будет иметь следующий вид:
|
un+1 −un |
un |
−un |
|
|
|
|||
|
m |
m |
+ |
m+1 m |
= 0 . |
|
(9) |
|
|
|
|
|
|
|
|
||||
|
|
τ |
|
h |
|
|
|
||
Подставляя |
гармоническое |
возмущение |
(7), |
получим |
|||||
λ−1 + exp(iωh)−1 = 0 , или λ = (1+ k )− k exp(iωh).
τ h
Получили на комплексной плоскости окружность радиуса k , центр которой находится в точке λ = (1+ k) , k > 0 . Поэтому условие устойчивости не вы-
полняется ни при каком k , т.е. τ .
105
Итак, показано, что для уравнения ∂∂ut + ∂∂ux = 0 , т.е. a > 0 , схема “явный ле-
вый уголок” устойчива при k = |
τ |
<1, а схема “явный правый уголок” неустой- |
||||||||
h |
||||||||||
|
|
|
|
|
|
|
|
|
||
чива ни при каких k . |
|
|
|
|
|
|
||||
Наоборот, для уравнения ∂u |
− ∂u = 0 аналог первой схемы всегда неустой- |
|||||||||
|
|
|
|
|
∂t |
∂x |
|
|
||
чив, а схема, аналогичная второй, устойчива при k ≤1 . |
|
|
||||||||
Упражнение. Проделать это самостоятельно. |
|
|
||||||||
Используя эти результаты, построим для уравнения |
∂u |
+ a ∂u = f схему, |
||||||||
|
|
|
|
|
|
|
|
∂t |
∂x |
|
допускающую изменение знака коэффициента a(x,t): |
|
|
||||||||
|
umn+1 −umn |
+ amn |
umn −umn −1 |
|
= fmn , если amn ≥ 0 . |
|
|
|||
|
τ |
h |
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
umn+1 −umn |
+ amn |
umn +1 −umn |
|
= fmn , если amn ≤ 0 . |
|
|
|||
|
τ |
h |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
Погрешность аппроксимации Ο(h + τ).
Схема устойчива, если k ≤1 .
106
