Лекция 7.

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ЧМ_Лекции2009.pdf

Скачиваний:

Добавлен:

05.06.2015

Размер:

1.42 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

состоит в том, чтобы разбить этот трудный вопрос на два

более простых:

Метод конечных разностей. Решение задачи Коши ОДУ.

Самым распространенным методом решения задач с ОДУ и ДУ с ЧП является метод конечных разностей. Во всех вариантах этого метода в области определения искомых функций вводится сетка, и решение ищется на сетке.

Для значений искомой сеточной функции строится система алгебраических уравнений, решение которой и служит приближенной таблицей значений решения исходной задачи.

Простейший способ построения этой системы алгебраических уравнений - разностной схемы - состоит в приближенной замене производных, входящих в ДУ и в краевые условия, разностными отношениями. Этим объясняется название метода - метод конечных разностей.

Задача Коши. Рассмотрим задачу Коши для системы:

dy (i)

− f (i) (x, y1,..., y(n) ) = 0

(1)

(i)

−заданные значения

(a) = ya

Система (1) может быть записана в векторной форме

y(1)

(x)

f (1)

(x, y(1)

,..., y(n) )

d y

− f (x, y) = 0

(2)

f =

...

,где y = ...

(n)

y(a) = ya

(x)

f (n) (x, y(1)

,..., y(n) )

Будем предполагать, что на [a;b] для задачи (1) выполнены условия суще-

ствования и единственности решения.

Обсуждение методов решения задачи Коши для простоты будем проводить на примере задачи для одного уравнения:

dy	− f (x, y) = 0,	a < x < b
			(3)

dx

y(a) = ya

Построение численных алгоритмов опирается на дискретизацию задачи.

Введем	в	области	расчета	x [a;b]	дискретный набор точек
ωh ={xk = a + hk;		k = 0,1,..., K; Kh = b −a} , в которых будем вычислять при-
ближенное решение.
Точки	xk будем называть узлами сетки,				h - шагом, совокупность узлов
ωh - сеточной областью.
Другие обозначения:
yh ={yk ,		k = 0,1,..., K} - совокупность искомых приближенных значений
решения задачи (3);
[ y]h ={y(xk ),		k = 0,1,..., K} - совокупность точных значений решения задачи
(3) в узлах сетки;
f h ={ f (xk , yk ),			k = 0,1,..., K}	- значения правой части в узлах.

Совокупность величин, отнесенных к узлам сетки, будем называть сеточными функциями. Т.о., сеточные функции являются элементами (K +1) -

мерного векторного пространства.

Введем погрешность численного решения

δh = yh −[ y]h ={yk − y(xk ), k = 0,1,..., K}.

Введем норму δh = max yk − y(xk ) .

Ставится вопрос о вычислении сеточной функцииyh , т.к. при измельчении сетки, т.е. при h →0 , она является все более полной таблицей искомого решения y(x) и дает о нем все более полное представление.

Пользуясь интерполяцией, можно было бы с возрастающей при h → 0 точностью восстановить решение y(x) всюду в области [a;b] . Ясно, что точность,

с которой это можно сделать при заданном фиксированном числе узлов и рас-

положении узлов сетки ωh зависит от дополнительных сведений о решении типа оценок его производных и расположения узлов сетки.

Рассмотрение вопроса восстановления функции по ее таблице составляет предмет теории интерполяции. Здесь рассматривается только задача вычисле-

ния таблицы yh .

Будем считать, что задача решена точно, если найдена сеточная функ-

ция[y]h . Однако ее вычислить точно нельзя. Вместо сеточной функции [y]h

вычисляется другая сеточная функция - yh . В связи с этим возникает вопрос о сходимости.

Определение. Будем говорить, что численное решение сходится к точно-

му, yk → y(xk ) , если δh →0 .
h → 0	h →0

Определение. Будем говорить, что метод, по которому получено решение,

является методом p −го порядка точности, δh ≤ const h p .

Итак, пусть дана задача Коши

dy		− f (x, y) = 0,	a < x < b (3)

	dx
y(a) = ya

Заменим производную по формулам численного дифференцирования. Метод Эйлера (явный).

k +1

− y

− f (xk , yk ) = 0

k = 0,1,..., K −1

(4)

y0 = ya

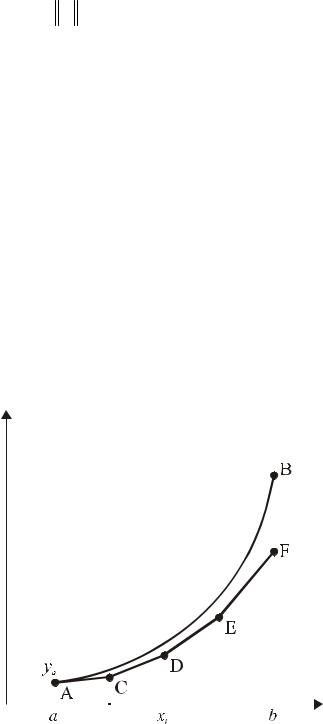
Рис. 7.1 Ломаная ABCDEF

В данном случае искомая интегральная кривая AB приближается к ломаной ACDEF (Рис. 7.1), наклон которой на элементарном участке [xk ; xk +1] оп-

ределяется наклоном интегральной кривой уравнения, выпущенной из точки(xk , yk ).

Последовательные значения получаются по формуле yk +1 = yk + h fk , кото-

рая сразу получается из уравнения.

Метод Эйлера (неявный). Заменяем производную левым разностным соотношением,

y	k	− y	k −1	− f (xk , yk ) = 0	k =1, 2,..., K
						(5)
		h

y0 = ya

Здесь при расчете слева направо возникают трудности, т.к. неизвестная величина yk входит в каждое уравнение нелинейным образом. Можно органи-

зовать итерационный процесс МПИ:

yk(s+1) = yk −1 + h f s (xk , yk ) = φ(s) ( yk ); yk(0) = yk −1;			s - порядок приближения.
Достаточное условие сходимости:
φ′y = h	f y′	x=xk <1, если h мало.


		y=yk

Определение.

Алгебраические соотношения между компонентами сеточной функции, которыми заменяют исходные ДУ в окрестности каждого узла сетки, называются разностными уравнениями.

Определение.

Замкнутую систему разностных уравнений (они разные при разныхh ) вместе с дискретизованными дополнительными (начальными или краевыми) условиями называют разностной схемой.

Таким образом, (4) – явная разностная схема Эйлера;

(5) – неявная разностная схема Эйлера.

Определение.

Если эта невязкаδφh

Определение.

Разностная схема называется явной, если система уравнений, определяющая эту РС, может быть записана в виде непосредственных расчетных формул для определения приближенных значений решения в узлах сетки.

Пример.
yk +1 = yk + h fk ,	yk , hk − известны k .

Если необходимо решать систему уравнений (линейных или нелинейных), для определения сеточных значений функции, то РС называют неявной.

Пример.

1)yk = yk −1 + h f (xk , yk )

2)	Ak yk −1 −Ck yk + Bk yk +1 = −Fk	k = 2,3,..., K −1
Итак, для задачи Коши записаны две разностные схемы. Общий вид:
L yh = φh . (*)
h
Нужно проверить являются ли		δh	= max	yk − y(xk )	→0 действительно
Нужно проверить являются ли		δh	= max	yk − y(xk )	→0 действительно
			k		h → 0
			k		h → 0

сходящимися.

Пусть задача (*) имеет единственное решение yh . Если бы при подстанов-

ке в левую часть (*) вместо yh сеточной функции [ y]h равенство оказалось бы в точности выполненным, то в силу единственности решения имело бы место

равенство yh =[y]h , при		δh	= 0 . Однако, как правило, систему (*) не удается

выбрать так, чтобы [ y]h	ей удовлетворяла в точности. При подстановке [ y]h в

уравнение возникает некоторая невязка

Lh [y]h = φh + δφh (**)

→0 , так что [ y]h удовлетворяет уравнению (*)

h → 0

все точнее, то будем говорить, что РС Lh yh = φh аппроксимирует дифференци-

альную краевую задачу Ly = φ на решении y этой дифференциальной краевой задачи.

В случае аппроксимации можно считать, что уравнение (**), которому удовлетворяет [ y]h , получается из уравнения (*) путем прибавления некоторой

малой (при малом h ) добавки δφh к правой части φh .

Следовательно, если решение yh задачи (*) устойчиво относительно из-

менений правой части ϕh , т.е. мало изменяется при изменении правой части,

то решение yh задачи L yh = φh	и решение [ y]h задачи (**) различаются мало,
h
так что из аппроксимации следует сходимость yh →[y]h приh → 0 .
Таким образом, путь	проверки сходимости	δh	→0 или
Таким образом, путь	проверки сходимости	δh	→0 или
			h → 0
			h → 0

•сначала проверить, имеет ли место аппроксимация задачи Ly = φ за-

дачей Lh yh = φh ;

•затем выяснить, устойчива ли задача Lh yh =ϕh .

•В этом содержится и указание на способы построения сходящихся РС

•для численного решения задачи Ly =ϕ :

•надо строить аппроксимацию ее РС;

•из многих возможных способов аппроксимации надо выбирать такие, при которых РС оказываются устойчивыми.

Замечание.

Понятие устойчивости введено неточно.

С самого начала предполагалось, что исходная задача корректна, т.е. имеет единственное решение, которое устойчиво по отношению к возмущениям входных данных: при малых возмущениях входных данных решение меняется мало.

Почему же проблема устойчивости возникает заново при переходе к РС, которой мы заменяем исходную задачу. Дело в том, что для исходной задачи значения решения в разных точках «жестко» связаны между собой ДУ, которым решение обязано удовлетворять.

После дискретизации, т.е. перехода к РС, значения разностного решения хоть и связаны (через разностные уравнения), но каждое из них вычисляется индивидуально. В расчет каждого привносится тем самым своя погрешность (за счет округлений при выполнении арифметических операций). Коррелируя друг с другом, эти погрешности при значительном количестве расчетных точек (узлов) могут быстро нарастать. Это и есть, в сущности, механизм возникновения неустойчивости при переходе к разностной задаче.

Особенно актуальными проблемы устойчивости становятся при численном решении ДУ в ЧП, т.к. сеточные области там становятся многомерными, каждый узел приобретает большое число соседних точек, следовательно, повышается вероятность неблагоприятной корреляции ошибок в этих точках.

Вернемся к явной схеме метода Эйлера для задачи Коши:

По определению погрешности:

yk = y(xk ) + δk ,

k = 0,1,..., K .

Подставляя

это

выражение

РС,

получим

y(xk +1) − y(xk )

δk +1 −δk

− f (xk , y(xk ) + δk ) = 0

По теореме Лагранжа о среднем (из мат. анализа):

- производная от

f по y в

f (xk , y(xk ) + δk ) = f (xk , y(xk ))+ ( f y′)k δk , где ( f y′)k

точке

(xk , y),

y(xk ) ≤ y ≤ y(xk ) + δk .

Перепишем уравнение в виде

k +1

−δ

y(x

k +1

) − y(x

)

−(f y′)

δk = −

− f (xk , y(xk ))

(6)

Решением (4)

является yh . При подстановке другой функции,

например

[y]h , возникает невязка, или погрешность аппроксимации

	y(x	k +1	) − y(x	k	)		k = 0,1,..., K −1 .
ψh = ψk =		k +1		k		− f (xk , yk ) ,
ψh = ψk =			h			− f (xk , yk ) ,
			h

Важно то, что погрешность численного решения, получаемая по сходящемуся методу, определяется погрешностью аппроксимации разностных урав-

нений, соответствующих этому методу.
Величину		ошибки		аппроксимации	нетрудно	оце-
нитьψk =	y(xk +1) − y(xk )		− f (xk , y(xk )) .
нитьψk =			− f (xk , y(xk )) .
	h
По	формуле		Тейлора,	предполагая	гладкость	функции,

y(xk +1) = y(xk )+ hy′(xk ) +	h2	~	~
	h2	~	~
		yk′′ , где	yk′′ = y′′		x [xk ;xk +h]	.
	2	yk′′ , где	yk′′ = y′′			.
	2			h
Отсюда, ψk =[y′(xk ) − f (xk , y(xk ))]+				h	~
					yk′′ или ψk =
				2	yk′′ или ψk =
				2

h ~′′ .

2 yk

Если

y′′

< M 2 , то

ψh

≤

M 2

M 2 = max

y′′

[a;b]

Явный метод Эйлера – метод 1-го порядка точности.

Другой метод:

k +1

− y

k −1

− f (xk

, yk ) = 0

- метод 2-го порядка точности

ψh

≤ C h2 .

= ya

= y

+ f (x

, y

)

MATLAB имеет множество функций для численного решения обыкновенных дифференциальных уравнений и их систем. Солверы ode23 и ode45 основаны на формулах Рунге-Кутты 2,3 и 4,5 порядков соответственно.

Метод Рунге-Кутты четвертого порядка (без вывода).