

Лекция 12.
Численное решения уравнения переноса.
На прошлой лекции было рассмотрено уравнение
∂∂Ut + ∂∂Ux = 0 ,
т.е. уравнение с a =1 > 0, f = 0 . Это линейное однородное уравнение с по-
стоянными коэффициентами. Были исследованы явные разностные схемы (PC) для задачи Коши
U (x,0) = φ(x) .
Необходимо научиться строить разностные схемы, решение которых сходилось бы к решению дифференциальной задачи.
Сходимость. Пусть дана дифференциальная задача
LU = f , x G ; LU = μ , x Г |
(1) |
Здесь Г = ∂G . |
|
Заменим задачу разностной схемой: |
|
Lh y = φ, x ωh ; Lh y = χ, x γh |
(2) |
Здесь ωh - сетка на области G , γh - сетка на границе области Г . |
|
Определение. Разностное решение |
y(x) сходится к решению U (x) задачи |
(1) , если

 y(x) −U (x)
y(x) −U (x)
 h →0 при h →0 .
h →0 при h →0 .
Разностное уравнение имеет порядок точности p, если
y(x) −U (x) |
|
|
|
h |
= O(h p ) при h →0 . |
|
|
||||
|
|
|
|
|
Замечание. В данном случае подразумевается согласованность нормы для непрерывных функций 
 •
•
 и для сеточных функций
и для сеточных функций 
 •
•
 h .
h .
107
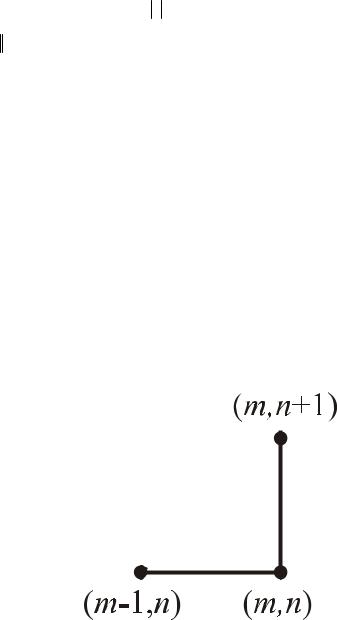
Понятие аппроксимации разностной схемы (2) дифференциальной задачи
(1) вводилась ранее. Возможна аппроксимация O(h),O(h2 ),...,O(1) . В последнем случае PC (2) не аппроксимирует ДЗ(1) . Порядок аппроксимации определяет-
ся наименьшим порядком аппроксимации в каждом узле. Если хотя бы в одном узле порядок аппроксимации есть O(1), то PC (2) не аппроксимирует ДЗ(1) .
Определение 2.
PC (2) устойчива, если разностное решение yn непрерывно зависит от φn и
χn :
M > 0, M ≠ M (h) : h , h < h0 :
~ |
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
+ M |
|
~ |
|
|
|
|
h . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y |
− y |
|
|
|
h |
≤ M |
|
|
|
φ−φ |
|
|
|
h |
|
χ |
−χ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Здесь φ~,~χ - малые возмущения правой части и граничных условий PC (2) ,
~y - возмущение решения.
Теорема(основная теорема теории разностных схем).
Если РС(2) устойчива и аппроксимирует ДЗ(1) на решении задачи, то она сходится; причем порядок точности определяется порядком аппроксимации. Иначе говоря, из аппроксимации и устойчивости следует сходимость.
Рассмотрим для уравнения переноса
∂U |
+ |
∂U |
= 0 |
(3) |
|
∂t |
∂x |
||||
|
|
|
шаблон “явный левый уголок” (Рис. 12.1)
Рис. 12.1 Шаблон “явный левый уголок”
108

Здесь сеткаxm = mh,tn = nτ.
На таком шаблоне РС будет иметь вид
|
U n+1 −U n |
|
|
|
U n −U n |
|
|
|
||||||||||||
|
|
m |
m |
+ |
|
m m−1 |
= 0 |
(4) |
||||||||||||
|
|
τ |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
h |
|
|
|
|||||||||
Такую РС мы называли РС №1. |
|
|||||||||||||||||||
Разложим Umn+1 |
и Um−1n в точке (m,n) в ряд Тейлора: |
|||||||||||||||||||
Umn+1 =Umn + τ∂U |
|
|
n |
+ |
|
1 |
|
τ2 ∂2U |
|
n |
+O(τ3 ) |
|
||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
∂t |
|
|
m |
|
|
2 |
|
|
∂t2 |
|
m |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Umn −1 |
=Umn − h∂U |
|
n |
+ |
|
1 |
h2 ∂2U |
|
n |
+O(h3 ) |
|
|||||||||
|
|
|
|
|||||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
∂x |
|
m |
|
|
2 |
|
∂x2 |
|
m |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя эти разложения в РС №1 и выделяя (группируя) ДЗ (1) в узле
(m, n) , получим:
( |
∂U |
+ |
∂U |
) |
|
n |
+ |
1 |
τ |
∂2U |
|
n |
− |
1 |
h |
∂2U |
|
n |
= 0 |
|
|
|
|||||||||||||||||
∂t |
∂x |
|
m |
2 |
∂t2 |
|
m |
2 |
∂x2 |
|
m |
||||||||
|
|
|
|
|
|
|
|
|
|
|
Если U C2 (x,t) , то(LU )h − LhUh = O(h + τ), т.е. имеет место первый порядок аппроксимации.
Практический прием отсеивания неустойчивых РС для эволюционных задач - метод гармонических возмущений.
Нелинейная задача линеаризуется, делается однородной, краевая задача заменяется задачей Коши и рассматриваются гармонические возмущения
U (x,t) = exp(μt) exp(iωx)
На сетке tn = nτ, xm = mh имеем: Umn = λn exp(iωmh), λ = exp(μτ) .
Условие устойчивости РС - не нарастание возмущений во времени, т.е. λ ≤1 .(Существует более слабое условие λ ≤1+C τ, но мы будем требовать
λ ≤1 ).
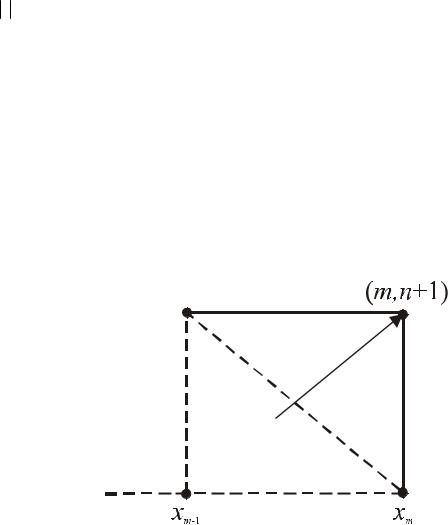
Для РС №1 (разность назад или “явный левый уголок”) при подстановке гармонического Umn в уравнение, получим:
λ = (1−k) + k exp(−iωh),k = hτ .
На комплексной плоскости Re λ, Im λ - это окружность радиуса k с цен-
тром в точке λ =1−k .
109
Из условия λ ≤1 получаем: РС №1 устойчива при k ≤1 и неустойчива при
k >1.
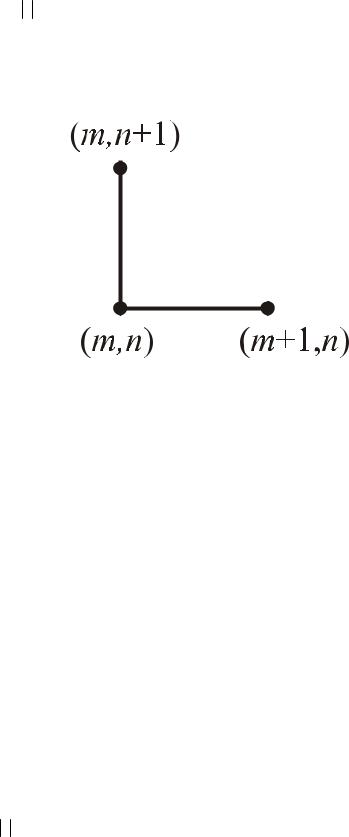
Рассмотрим РС №2.
Разность вперед, или шаблон “явный правый уголок” (Рис. 12.2)
Рис. 12.2 Шаблон “явный правый уголок”
Этому шаблону соответствует уравнение
U n+1 −U n |
U n −U n |
|
|||
m |
m |
+ |
m+1 m |
= 0 |
(5) |
|
|
|
|||
|
τ |
h |
|
||
Эта РС №2 аппроксимирует ДЗ (3) в узле (m,n) с первым порядком по h и
τ , т.е. O(h + τ) . Это легко показать, разлагая Umn+1 и Um+1n в ряд Тейлора в узле
(m, n) .
Рассмотрим устойчивость к гармоническим возмущениям:
Umn = λn exp(iωmh), |
λ = exp(μτ) . |
|
|
|||||
Получим: |
|
|
|
|
|
|
||
|
λ −1 |
+ |
exp(iωh) −1 |
|
= 0 , или λ = (1+ k) − k exp(iωh),k = |
τ |
. |
|
|
τ |
|
|
h |
|
|
h |
|
Геометрическая интерпретация - окружность радиуса k |
с центром в точке |
|||||||
λ =1+ k .
Условие λ ≤1 - РС №2 неустойчива ни при каком k > 0 .
Замечание 1.
Эволюционная РС называется явной, если значения функции на новом слое вычисляются по непосредственной формуле через значения функции на
110
нижнем слое. Если же для вычисления значений U n+1 приходится решать уравнения и связи, то РС называется неявной.
Замечание 2.
Если бы мы рассматривали уравнение
∂∂Ut − ∂∂Ux = 0 , где a = −1 < 0 ,
то условие устойчивости было бы обратным:
k ≤1 для РС №2 и неустойчивость ни при каком k для РС №1. Проанализируем это еще раз на геометрической интерпретации устойчи-
вости.
Геометрическая интерпретация устойчивости.
Рассмотрим для простоты только устойчивость по начальным данным.
Пусть f = 0 , ∂∂xt = a = Const . Характеристики - прямые линии x − at = Const .
В этом случае U (x,t) = (x − at) , происходит перенос тепла (вещества) вдоль характеристик без изменения.
Корректность дифференциальной задачи:
Малым изменениям входных данных соответствуют малые изменения решения.
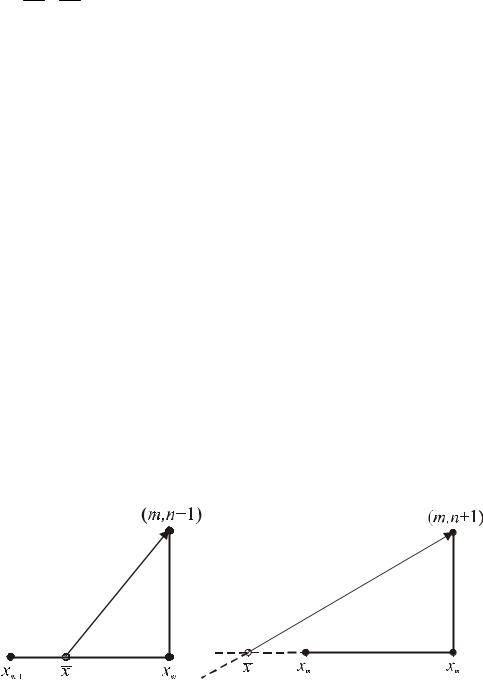
Рассмотрим теперь РС №1 и характеристику, приводящую в точку
(xm ,tn+1) из x ,
x = xm −at . См. Рис. 12.3
Рис. 12.3.
РС №1
Запишем для y(x) формулу линейной интерполяции:
111

y(x) = ym−1 |
xm − x |
+ ym |
x − xm−1 |
= |
aτ |
ym−1 + (1 − |
aτ |
) ym |
|
|
h |
|
h |
|
|
||||||
|
|
h |
|
|
|
h |
|
|||
Значение ymn+1 ≡ y(x) . |
|
|
|
|
|
|
|
|
|
|
1) если aτ< h (k <1) , xm−1 ≤ x ≤ xm , интерполяция. |
|
|||||||||
Значение x определяется по xm−1 |
и по xm . РС устойчива. |
|
||||||||
2) если aτ > h (k >1) , x < xm−1 , экстраполяция. |
|
|||||||||
РС неустойчива. |
|
|
|
|
|
|
|
|
|
|
Действительно, ДУ: в |
(xm ,tn+1) |
значение приходит только из x,tn . Если |
||||||||
x [xm−1, xm ], то решение |
U C1 может |
сильно меняться на [xm−1, xm ], |
но |
|||||||
Umn+1 =U (x,t) . Но РС: ymn+1 |
сильно меняется (по изменившимся ym−1n и ymn |
), |
||||||||
ymn+1 не может сходится к Umn+1 . |
|
|
|
|
|
|
|
|||
|
|
|
Неявные схемы. |
|
||||||
РС №3. С помощью трехточечного шаблона “неявный левый уголок” (Рис 12.4) построим схему:
|
Umn+1 −Umn |
+ |
Umn+1 −Um−1n+1 |
= 0 |
|
(РС №3) |
|||
τ |
|
|
|
h |
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 12.4 Шаблон “неявный левый уголок”
Разлагая функцию в ряд Тейлора в точке (m, n +1) , нетрудно показать, что ошибка аппроксимации в данном случае также O(τ+ h) .
Исследуя устойчивость методом гармонических возмущений, находим
λ−1 + λ − λexp(−iωh) = 0
τ h
λ[1+ k −k exp(−iωh)]=1
112
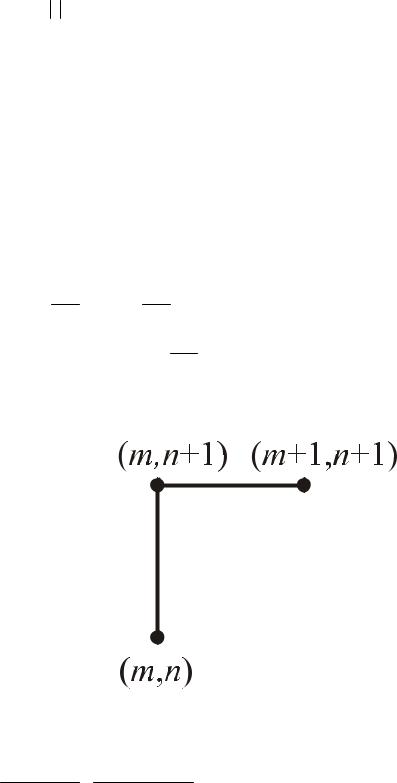
λ =[1+ k −k exp(−iωh)]−1 .
Модуль выражения, стоящего в квадратных скобках, всегда не меньше единицы.
(Действительно, окружность радиуса k с центром в точке λ =1+ k ). Поэтому λ ≤1 и схема безусловно устойчива для любых k , а значит и τ .
Формулы на неизвестном верхнем слое можно записать в виде:
− k Um−1n+1 +(1+ k) Umn+1 =Umn m = 2,3,..., M
Так как a =1 > 0 , то граничные условия задаются на левой границе, т.е. при
m =1.
Поэтому U1n+1 можно считать известной.
Далее для m = 2,3,..., M величины Um могут быть последовательно вычис-
лены из уравнения:
Umn+1 = 1+k k Um−1n+1 + 1+1 k Umn
Прогонка устойчива, т.к. k k+1 <1. РС №4.
Рассмотрим теперь неявную схему “неявный правый уголок” (Рис 12.5)
Рис. 12.5 Шаблон “неявный правый уголок” РС для этого шаблона (РС №4):
Umn+1 −Umn + Um+1n+1 −Umn+1 = 0
τh
113
Разлагая Umn и Um+1n+1 в ряд Тейлора в окрестности точки (m, n +1) , полу-
чим что ошибка аппроксимации РС №4 также O(τ+ h) .
Исследуя устойчивость методом гармонических возмущений
Umn = λn exp(iωmh) , λ = exp(μτ) , получим λ =[1−k + k exp(iωh)]−1
Пользуясь геометрической интерпретацией и результатом оценки устойчивости предыдущей РС, получим:
λ ≤1 , если k ≥1 !!!
(обратите внимание на знак неравенства) Прогоночные формулы имеют вид:
Um+1n+1 = |
k −1 |
Umn+1 |
+ |
1 |
Umn . |
|
|
|||
|
|
|
|
|||||||
|
k |
|
k |
|
|
|
|
|||
|
k −1 |
|
, т.е. k ≥1 . |
|||||||
Прогонка устойчива при |
<1 |
|||||||||
k |
|
|||||||||
|
|
|
|
|
|
|
|
|||
Геометрическая интерпретация (устойчивости схемы, построенной по шаблону “неявный левый уголок” (Л12 Рис. 12.6), схему, построенной по шаблону “неявный правый уголок” (Л12 Рис. 12.7)).
Рис. 12.6 РС №3 ( k ≥1 - условие устойчивости)
114
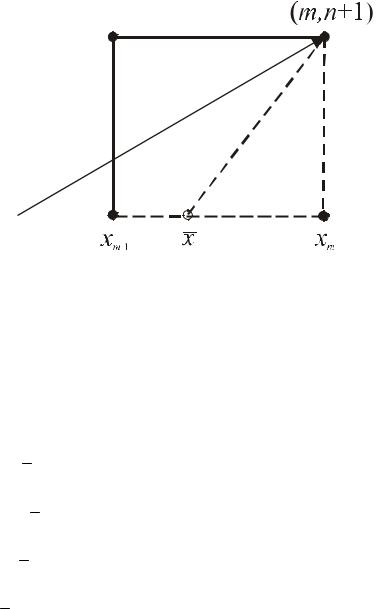
Рис. 12.7 РС №4 (устойчива при k )
Комбинированные аппроксимации.
В тех случаях, когда коэффициент a(x,t) по абсолютной величине изменя-
ется в широких пределах или меняет знак, могут быть полезны комбинации из различных схем, например:
1)если 0 ≤ amn hτ ≤1, то РС №1 (левый явный уголок)
2)если −1 ≤ amn hτ ≤ 0 , то РС №2 (правый явный уголок)
3)если 1 ≤ amn hτ , то РС №3 (неявный левый уголок)
4)если amn hτ ≤ −1 , то РС №4 (неявный правый уголок)
Реализация подобных комбинированный схем вызывает лишь несущественные технические трудности.
На очередном временном слое расчетная область делится на подобласти, в каждой из которых действует одна какая - либо РС.
Искомая функция сначала определяется в областях, где действуют явные схемы.
Затем в подобластях, где действуют неявные схемы, выполняются прогонки. Граничными условиями для них являются значения функций, вычисленных по явным схемам. Прогонки выполняются с учетом знака коэффициента
a .
Схемы с центральными разностями.
115

Рассмотренные неявные схемы РС №4 и РС №3 учитывают расположение характеристик или в самой конструкции схемы или в ее способе реализации.
Напишем формулы для двух РС, не зависящие (по крайней мере формально) от направления характеристик.
|
|
Umn+1 −Umn |
+ amn |
Um+1n+1 −Um−1n+1 |
= fmn |
|
|
|
|
|
|
(РС №5) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
τ |
|
|
|
|
|
2h |
|
|
|
|
|
|
|
|
|
|
|
|
U |
n+1 −U |
n |
|
U |
n+1 |
−U |
|
n+1 |
U |
m+1 |
n −U |
m−1 |
n |
|
|
||||||
|
|
|
m |
m |
|
+ 0,5amn |
|
m+1 |
|
m−1 |
+ |
|
|
|
|
= fmn |
(РС №6) |
||||
|
|
|
τ |
|
|
|
2h |
|
|
|
2h |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ошибка аппроксимации РС №5 |
есть O(τ+ h2 ) , РС №6 - O(τ2 + h2 ) . |
||||||||||||||||||||
Легко проверить, что обе схемы безусловно устойчивы, т.е. устойчивы
τ( k) .
Система уравнений на верхнем слое имеет 3 - х диагональную матрицу. Если граничные условия известны и слева и справа, то выполняется трехточечная прогонка. Если же одного из граничных условий нет (а это обычно, т.к. характеристики с одной стороны всегда выходят из области), то с этой стороны следует записать дополнительное сеточное граничное условие, воспользовавшись неявной схемой, шаблон которой содержит два узла на верх-
нем слое.
Сравнение явных и неявных схем.
Условие Куранта, обеспечивающее устойчивость явных схем, ограничива-
ет шаг по времени τ ah . Это ограничение является естественным с точки зре-
ния истинно нестационарных решений, зависящих от t также сильно, как и от
x .
Действительно, рассмотрим решение U = (x − at) уравнения |
∂U |
+ a |
∂U |
= 0 , |
|||||
∂t |
∂x |
||||||||
|
|
|
|
|
|
|
|||
a > 0, a = Const , f |
= 0 . Для схем явный левый уголок или неявный левый |
||||||||
уголок погрешность аппроксимации есть сумма двух слагаемых: |
|
|
|
||||||
Eτ = |
a2τ |
′′ и Eh = |
ah |
′′ . |
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
2 |
|
|
|
|
|
|||
При оптимальном соотношении должно быть Eτ Eh (иначе один из шагов можно было бы увеличить).
116

Отсюда следует k = ahτ 1 .
Для квазистационарных решений, слабо зависящих от времени, условие Куранта может быть чрезмерно жестким с точки зрения требований точности.
При расчете квазистационарных решений целесообразно применять неявные схемы.
117

Лекция 13.
Численное решение уравнений теплопроводности.
Процесс распространения тепла на прямой описывается уравнением теплопроводности
|
|
|
∂u |
|
∂ |
|
∂u |
|
|
|
|
|
||
|
|
|
|
+ f , где u(x,t) - температура. |
(1) |
|||||||||
cρ |
|
= |
|
|
k |
|
|
|||||||
∂t |
∂x |
|
||||||||||||
|
|
|
|
|
∂x |
|
|
|
|
|
||||
c - теплоемкость единицы массы; |
|
|||||||||||||
ρ - плотность; |
|
|
|
|
|
|||||||||
k |
- коэффициент теплопроводности; |
|
||||||||||||
|
|
|
- плотность тепловых источников. |
|
||||||||||
|
f |
|
||||||||||||
Коэффициенты k и c |
могут зависеть не только от x и t , но и от темпера- |
|||||||||||||
туры u . (В этом случае уравнение называется квазилинейным). |
|
|||||||||||||
Если коэффициенты k |
и cρ постоянны, то уравнение (1) можно перепи- |
|||||||||||||
сать в виде: |
|
|
|
|
|
|
|
|
||||||
|
|
|
∂u |
= a2 |
∂2u |
|
~ |
|
|
|
(2) |
|||
|
|
|
∂t |
∂x2 |
+ f |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
или, без ограничения общности |
|
||||||||||
|
|
|
∂u |
= |
∂2u + f |
|
|
|
|
(3) |
||||
|
|
|
∂t |
|
∂x2 |
|
|
|
|
|
|
|
||
из (2) в (3) можно перейти заменой переменных x'= ax .
Если ищется решение уравнения (2) на отрезке 0 ≤ x ≤ l , то обычно поль-
зуются безразмерными переменными x'= |
x |
, |
t'= |
a2t |
. |
||||
l |
|
||||||||
|
|
|
|
|
|
|
l2 |
||
В этих |
переменных уравнение (2) |
записывается в виде (3), причем |
|||||||
|
|
l |
2 ~ |
|
|
|
|
|
|
0 ≤ x'≤1, |
f = |
f |
. |
|
|
|
|
||
a2
Рассмотрим первую краевую задачу для уравнения (3) в прямоугольнике
G = (0 ≤ x ≤1, 0 ≤ t ≤T ) .
118
|
Требуется |
найти |
непрерывное |
в G решение |
u = u(x,t) |
задачи |
||||||
∂u |
= |
∂2u + f (x,t) , |
0 ≤ x ≤1, |
0 ≤ t ≤T |
, удовлетворяющее начальным и гра- |
|||||||
∂t |
|
∂x2 |
|
|
|
|
|
|
|
|
|
|
ничным условиям |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
u(x,0) = u0 (x), |
0 ≤ x ≤1 |
|
|
|
|
|
|
|
|
|
|
|
u(0,t) = u1(t), |
u(1,t) = u2 (t), |
0 ≤ t ≤T . |
|
|
|
||
|
Запишем семейство шеститочечных схем в сеточной области ωhτ , |
покры- |
||||||||||
вающей область G : |
|
|
|
|
|
|
|
|
||||
|
|
xm = mh; |
m = 0,..., M ; tn = nτ; |
n = 0,..., N; |
h = |
1 |
; |
τ = |
T |
. |
||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
MN |
|
N |
||
|
|
umn+1 −umn |
+ Λ(σumn+1 + (1−σ)umn ) + φmn |
|
|
|
|
(4) |
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
τ |
|
|
|
|
|
|
|
|
|
|
Здесь используется шеститочечный шаблон (Рис. 13.1).
Рис. 13.1 Шеститочечный шаблон Разностный оператор Λ означает трехточечную разностную аппроксима-
цию второй производной по координате:
|
Λum = |
um+1 − 2um +um+1 |
. |
|
||||||
|
|
|
||||||||
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
∂2u |
|
+ Ο(h |
2 |
). Разностную схему (4) будем |
||
|
|
|
|
|
2 |
|
||||
Как мы выяснили ранее, Λum = |
∂x |
|
|
|||||||
|
|
|
|
|
m |
|
|
|
|
|
называть схемой с весами. σ - параметр (вес). |
|
|
||||||||
Краевые и начальные условия аппроксимируем точно: |
||||||||||
u0n = u1(tn ), |
uMn = u2 (tn ), |
um0 = u(xm ,0)= u0 (xm ). |
||||||||
Для mn можно взять φmn |
= f (xm ,tn+0.5 ), |
|
tn+0.5 = tn + 0.5τ. |
|||||||
Множество узлов сетки ωhτ , лежащих на прямой t = tn , обычно называют слоем (или временным слоем).
119
Схема (4) содержит значения искомой функции umn на двух слоях и поэто-
му называется двухслойной схемой. От выбора параметра σ зависит точность и устойчивость РС (4), а также способ ее реализации.
Рассмотрим схемы, соответствующие частным значениям параметра σ . 1. При σ = 0 получаем четырехточечную схему:
umn+1 −umn |
= Λumn + φmn , |
(5) |
|
τ |
|||
|
|
построенную по четырехточечному шаблону, изображенному на Рис. 13.2
Рис. 13.2 Явная четырехточечная схема.
Или |
|
|
|
|
umn+1 = (1− 2kП )umn + kП(umn −1 +umn +1 )+ τφmn |
|
|
|
|
|
(5’) |
||||||||||||||||||
kП = |
|
τ |
|
, значение umn+1 |
|
в каждой точке t = tn+1 |
выражается по явной фор- |
||||||||||||||||||||||
|
h2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
муле (5’) через значения umn |
на слое t = tn , т.е. на старом временном слое. Это |
||||||||||||||||||||||||||||
явная схема. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Аппроксимация. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Если у функции u(x,t) существуют требуемые производные, то |
|||||||||||||||||||||||||||||
n |
|
|
|
un |
|
− 2un |
+un |
|
|
∂2u n |
+ Ο(h |
2 |
). |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
m+1 |
|
m |
|
m−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Λum |
= |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
h |
2 |
|
|
|
∂x |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
un+1 |
−un |
|
|
∂u n |
|
1 |
|
∂2u |
n |
|
|
|
(Lu) |
|
|
|
= Ο(h2 + τ). |
|||||||||
Далее, |
|
|
|
|
m |
|
m |
= |
+ |
|
|
|
τ |
|
|
, таким образом |
− L u |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
τ |
|
|
∂ m |
|
2 |
|
∂t |
2 |
|
|
|
|
n |
n |
n |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|||||||||
Схема второго порядка аппроксимации по пространственной координате и первого - по временной.
120

Устойчивость.
Метод гармонических возмущений.
umn = λn exp(iωmh), λ = exp(μτ) , подставляя эту гармонику в РС (5), получим
λ= (1− 2kП )+ kП(exp(−iωh)+ exp(iωh)) или, т.к. exp(−iωh)+ exp(iωh)= 2cos(ωh),
λ=1− 2kП(1−cos(ωh))=1− 4kП sin2 ω2h =1− 4kПz , где kП = hτ2 , z = sin2 ω2h .
Условие устойчивости |
|
λ |
|
≤1 или −1 ≤1− 4kПz ≤1, отсюда |
kП ≤ |
1 |
или τ ≤ |
h2 |
. |
|
|
||||||||
|
|
|
|
||||||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
||||
Это довольно жесткое ограничение на шаг по времени τ . (Например, в ги-
перболическом уравнении переноса |
aτ |
<1, |
τ < |
h |
, |
т.е. ограничение τ ~ h ). Здесь |
|||||||||
h |
a |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
ограничение τ ~ h2 . Если h достаточно малое |
|
|
1 |
, |
1 |
, |
1 |
|
, то ограниче- |
||||||
|
|
|
|
|
|
|
|||||||||
40 |
100 |
500 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
ние на шаг по времени довольно обременительное (очень долго считать). Тем не менее, можно показать, что явные схемы обладают всеми “хорошими” свойствами, соответствующими дифференциальной краевой задаче:
• свойством позитивности (u(x,t)n > 0 h, τ)
•свойством монотонности
•простота реализации.
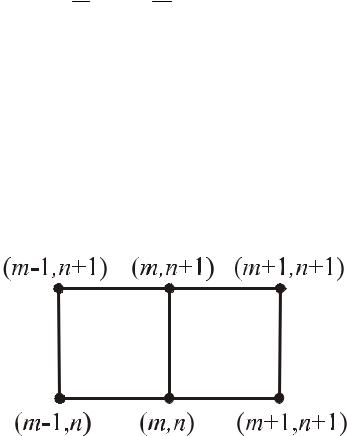
Это оставляет за явными схемами определенную сферу их применимости. σ =1. В этом случае получаем неявную четырехточечную схему:
umn+1 −umn |
= Λumn+1 + φmn , |
(6) |
|
τ |
|||
|
|
построенную по четырехточечному шаблону, изображенному на Рис. 13.3
Рис. 13.3 Неявная четырехточечная схема
121
Эта схема также имеет порядок аппроксимации Ο(h2 + τ), чтобы это прове-
рить, можно выполнить разложение в ряд Тейлора. Устойчивость.
λ = (1+ 4kПz)−1 , где kП = hτ2 , z = sin2 ω2h .
Эта схема является устойчивой при всех значениях kП , причем с ростом kП (т.е. τ ) , стабилизирующие свойства РС будут увеличиваться. Тем не менее
надо соблюдать требования аппроксимации. |
|
||||||||||
|
2. σ = |
1 |
. |
|
Неявная |
шеститочечная |
симметричная схема: |
||||
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
umn+1 −umn |
= |
|
1 |
Λumn+1 |
+ |
1 |
Λumn + φmn |
, |
(7) |
|
|
|
2 |
2 |
||||||||
|
τ |
|
|
|
|
|
|||||
построенная по шеститочечному шаблону, изображенному на Рис. 13.4.
Рис. 13.4 Неявная шеститочечная симметричная схема
Схема имеет порядок аппроксимации Ο(h2 + τ2 ), чтобы это проверить, не-
|
|
|
|
|
|
1 |
|
|
обходимо разложить в ряд Тейлора в окрестности точки m,n + |
|
. |
||||||
2 |
||||||||
|
|
|
|
|
|
|
||
Устойчивость. |
|
|
|
|
|
|
|
|
λ = (1− 2kПz)(1+ 2kПz)−1 , где kП = |
τ |
, |
z = sin2 |
ωh |
. |
|
|
|
h2 |
|
|
|
|||||
|
|
2 |
|
|
|
|||
Устойчивость также безусловная, т.е. устойчива при всех kП , а значит и τ .
Заметим, однако, что при больших значения kП в области высоких частот ве-
личина λ ~ −1 и стабилизация слабая и немонотонная, что создает предпосыл-
122

ки для немонотонного профиля, а также для нежелательных резонансных явлений.
РС из 2. и 3. реализуются с помощью алгоритма прогонки.
Аппроксимация по времени. При решении задачи по
1)явной схеме, с выполнением условия устойчивости;
2)неявной схеме, со значительно большим шагом по времени τ . Ввиду простоты задачи и возможности ее реализации обоими способами
следует сравнить решения при одном и том же физическом времени t . В результате выяснится погрешность, вносимая аппроксимацией по времени
Ο(h2 + τ2 ), монотонность и немонотонность пространственного профиля. Вы-
яснится |
|
константа, стоящая при Ο(τ) или Ο(τ2 ), т.е. M 2 |
= max |
∂2u |
или |
|||
|
|
|
|
|
|
t(x) |
∂t2 |
|
M 4 |
= max |
|
∂4u |
|
. |
|
|
|
|
|
|
|
|
||||
|
t(x) |
|
∂t4 |
|
|
|
|
|
Следует понимать, что хотя условие безусловной устойчивости и не накладывает ограничений на шаг по времени τ , ограничения на него остаются из условий аппроксимации разностной схемой дифференциальной краевой задачи. Кроме того, при увеличении τ в неявной схеме возрастает опасность возникновения немонотонности пространственного профиля.
Сходимость решения по сетке.
При выполнении курсовой работы необходимо исследовать сходимость решения по сетке. Для этого при заданной величине физического времени для эволюционной задачи или для стационарной задачи следует сравнить решение, полученное на системе вложенных сеток (например, на общих узлах се-
ток h, h2 , h4 или h, h4 ,16h ).
В отсутствии аналитического решения задачи сходимость решения по сетке к некоторому определенному решению часто служит единственным доказательством безошибочности РС и правильности полученного решения. Более
123
того, ввиду отсутствия прямых способов доказательства правильности полученного решения сходимость решения по сетке - косвенный способ доказательства - обычно принимается как достаточный способ доказательства правильности полученного решения.
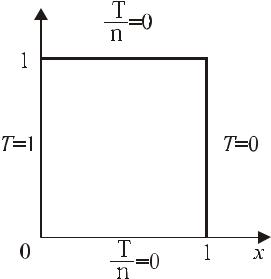
В качестве иллюстрации пример из научной работы.
Решается система двумерных уравнений Навье-Стокса – сложных нелинейных уравнений с малым параметром при старшей производной (т.е. с пограничным слоем). У этой системы уравнений нет и не может быть аналитических или даже автомодельных решений. Тогда все специалисты, которые решают такие задачи, договорились и решили тестовую задачу - задачу конвективного течения в квадратной области с заданным перепадом температур
(Рис. 13.5) при разных числах Рэлея: (безразмерные пере-
менные).
Рис. 13.5 Область решения модельной задачи
После этого была проведена международная конференция, на которой все предъявили свои результаты и выработали приблизительно точное решение этой задачи. После этого каждый, кто публиковал какие-либо данные, основанные на расчетах своих двумерных или двумерных ассиметричных уравнений Навье-Стокса, должен был сначала предъявить свое решение тестовой задачи. Если его результаты хорошо совпадали с “точным” решением тестовой
124
задачи, выработанным на конференции, то читатели с доверием относились к его численным расчетам.
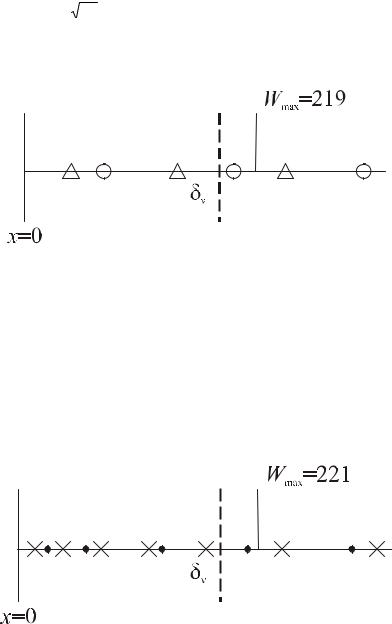
Для примера остановимся на одном результате, полученном при выполнении этой тестовой задачи. Методом установления рассчитывается интенсив-
ное течение жидкости при большом числе Рэлея, (т.е. большой перепад температур слева и справа). Течение жидкости характеризуется относительным покоем в центре и очень быстрым движением вблизи пограничных слоев. Ищется максимум скорости W , который достигается вблизи погранич-
ного слоя толщины δν ~ |
1 |
, около стенки x = 0 . |
|
Re |
|||
|
|
Решение тестовой задачи было предложено искать на равномерных сетках
81×81 и 61×61 (см. Рис. 13.6 )
Рис. 13.6 Расположение узлов равномерных сеток 81×81( )и 61×61(Ο)в
тестовой задаче
Вычислительная техника того времени не позволяла применять столь частые (равномерные) сетки, какие использовали зарубежные специалисты. Поэтому было принято решение использовать неравномерные сетки, сгущающиеся от центра области к твердым стенкам 41×41 и 35×35 (Рис. 13.7)
Рис. 13.7 Расположение узлов неравномерных сеток 41×41(×) и 35×35 (•) в
тестовой задаче
125
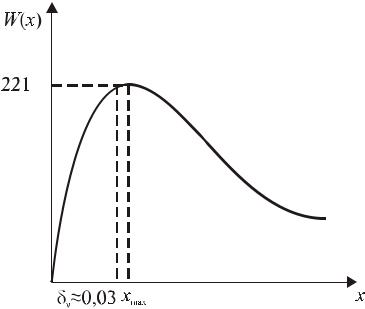
Чтобы вычислить более точную координату и величину максимума скорости W , применялась пятиточечная интерполяция по узлам, ближайшим к максимальному значению. Поскольку на равномерных сетках при этом захватывались узлы, лежащие в середине области, то получился максимум, несколько заниженный по сравнению с интерполяцией по узлам неравномерных сеток. Таким образом, несмотря на менее производительную вычислительную технику, удалось несколько уточнить координату и величину этой тестовой характеристики. (Рис. 13.8)
Рис. 13.8
Итак, необходимо проверять сходимость решения по сеткам к некоторой сеточной функции.
126
