Лекция 4.

Многочлены Чебышева. Интерполяция функции. Среднеквадратичное приближение. Метод наименьших квадратов.

Многочлены Чебышева.

Определение.

На отрезке [−1,1] определим многочлены Чебышева:

Tn (x)= cos(n arccos(x)), n = 0,1,2,... ; (1)

Найдем несколько первых многочленов:

T0 (x)=1

T1 (x)= cos(arccos(x))= x .

Т.к. 2 cos(φ) cos(n φ)= cos((n +1) φ)+ cos((n −1) φ) то cos((n +1) φ)= 2 cos(φ) cos(n φ)− cos((n −1) φ) (2)

Полагая в формуле (2) φ = arccos(x), получим

Tn+1 (x)= 2x Tn (x)−Tn−1 (x) (3) .

Получена рекуррентная формула для полиномов Чебышева. Отсюда следует, что Tn (x) - полиномn – ой степени.

Последовательно получаем:

29

2.T2n (x)- четные функции; T2n−1 (x)- нечетные функции.

3.Коэффициент при старшей степени xn многочлена Tn (x) равен 2n−1

(доказательство по индукции).

4. Многочлен Tn (x) имеет на интервале (−1,1) ровно n различных действи-

тельных корней, определяемых формулой:

Благодаря свойству 6. многочлен

отклоняющимся от нуля.

Полиномы Чебышева, нормированные таким образом, чтобы коэффициент при старшей степени x был равен 1:

Можно записать полином степени n , наименее отклоняющийся от нуля на произвольном отрезкеx [a, b] x = a +2 b + b −2 a t t [−1,1].

Применение полиномов Чебышева к задаче интерполяции.

Задача. Оптимизировать интерполяцию полиномом Лагранжа с помощью выбора узлов интерполяции.

30

Если узлы интерполяции выбрать как у полиномов Чебышева, т.е. в точ-

Вывод.

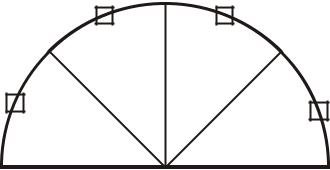
Геометрическая интерпретация корней полинома Чебышева: если верх-

нюю полуокружность единичного радиуса разделить на n частей, то середины дуг – координаты нулей, экстремумы – точки деления (См Рис.4.1

Рис. 4.1 Геометрическая интерпретация корней полинома Чебышева

31

Равномерное приближение функций на отрезке.

Пусть f (x)- достаточно гладкая, т.е. f (n+1)(x) ≤ M . Тогда найдется такое n

(степень интерполяционного полинома), что выполняется условие:

ε > 0 : f (x)− Pn (x) C ≤ ε

Пример.

f (x)= x + 2, x [−1,1]. Приблизить многочленом n - ой степени так, чтобы выполнялось условие: f (x)− Pn (x) C ≤ ε =10−3 . Найти n .

Решение.

f (x) C ∞ [−1,1]. Возьмем для интерполяции ИП Лагранжа, построенный по

нулям полинома Чебышева € ( ). Имеем:

Tn+1 x

Непосредственным подбором можно убедиться, что n = 4 удовлетворяет этому условию.

Для произвольной функции f (x), недостаточно гладкой, задача становится

гораздо сложнее.

32

Среднеквадратичное приближение. (Метод наименьших квадратов.) Рассмотрим принципиально иной способ приближения функций, задан-

ных таблицей своих значений

{fi , i = 0,1,..., n}в точкахxi . Будем искать приближение в виде полинома сте-

пениm :

Pm (x)= a0 + a1x + am xm , такого, который минимизирует сумму квадратов от-

клонений полинома от заданных значений функции:

Ясно, что при m = n решением задачи является ИП, поскольку на нем достигается абсолютный минимум: Φ ≡ 0 .

Известно, что при m ≤ n задача имеет единственное решение.

При m > n задача имеет бесконечное множество решений (т.е. абсолютный минимум величиныΦ): произвольные n +1 коэффициентов определяются из условий интерполяции, остальные полагаются равными нулю.

Рассмотрим случайm < n . Условия минимума функции Φ следуют из математического анализа:

Для определения коэффициентов {a0 , a1 ,..., am } получается замкнутая сис-

тема линейных алгебраических уравнений с симметрической матрицей.

Элементы матрицы вычисляются через координаты табличных точек. Правые части системы определяются заданными табличными значениями.

33

Полином степени m < n с коэффициентами, найденными таким образом,

называется среднеквадратичным приближением функции, заданной таблицей. (Или наилучшим среди полиномов степени m приближением к функции по табличным данным.)

Соответствующую погрешность приближения можно характеризовать

Основная сфера применения – обработка экспериментальных данных.

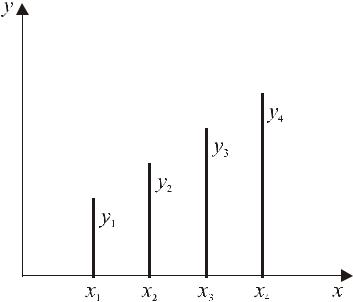
Рис.4.2 Экспериментальные данные

Экспериментальные данные характеризуются значительным разбросом (ошибки измерения, экспериментальный “шум” и т.д.) Интерполяционный полином, построенный по этим точкам, плохо отражает поведение функции f (x). Среднеквадратичный полином “сглаживает шум”.

Упрощенный взгляд на метод наименьших квадратов. Примеры. Пусть известно, что величина y является некоторой функцией от аргумен-

таx , причем в результате измерений получена таблица значений yk = y(xk ), k =1,2,3,4

Полученные измерения позволяют приближенно считать, что зависимость y = y(x) является линейной, т.е.

34

Получилась система четырех линейных уравнений относительно двух неизвестных a1 , a2 . Классического решения данной системы нет.

4

Введем функциюΦ(a1 , a2 )= ∑a1 xk + a2 2 , равную сумме квадратов невязок,

k=1

ипримем за обобщенное решение системы ( ) ту пару чисел(a1 , a2 ), для ко-

торой функция Φ(a1 , a2 ) принимает наименьшее значение. Получим систему двух уравнений:

Выбор функции Φ(a1, a2 ), от которой зависит решение (пара чисел a1, a2 )

несколько произволен. Можно было бы придать каждому значению функции свой весbk (k =1,2,3,4), тогда получилась бы формула:

k =1

было бы другим.

Примеры метода наименьших квадратов для определения обобщенного решения системы 4-х уравнений( ).