

Лекция 5.
Кусочная интерполяция. Численное дифференцирование (ЧД).
|
|
|
|
|
|
Кусочная интерполяция (КИ). |
|
|
|
|
|
|||||||||||
Оценка погрешности интерполяции функции f (x) |
с помощью ИП Pn (x) |
|||||||||||||||||||||
составляет: |
|
R (x) |
|
= |
|
f (x)− P |
(x) |
|
≤ |
M n +1 |
|
|
ω |
|
(x) |
|
, где M n+1 |
= max |
|
f (n+1)(x) |
|
- полу- |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
n |
|
|
|
n |
|
|
|
(n +1)! |
|
|
n +1 |
|
|
|
x [a;b] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
чена в предположении существования |
(n +1) -ой непрерывной производной |
|||||||||||||||||||||
функции f (x). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Далеко не всегда приходится иметь дело с очень гладкими функциями. В связи с этим часто применяется кусочная интерполяция - для приближения функции в точке x строится полином невысокой степени по данным в табличных точках, ближайшим к т. x .
Пример.
Необходимо вычислить f (x) для x [xi ; xi+1 ].
Кусочно-линейная интерполяция
Для вычисления f (x) используется линейное приближение
f (x) ≈ fi + fi +1h− fi (x − xi ), где h = xi+1 − xi .
Очевидно, что при подстановке x = xi или x = xi+1 получается тождество.
Кусочно-квадратичная интерполяция.
Привлекается еще одна табличная точка ( xi−1 или xi+2 ), и строится поли-
ном второй степени:
f (x) ≈ f |
i |
+ |
fi+1 − fi |
(x − x |
) + |
fi+1 − 2 fi + fi−1 |
(x − x )(x − x |
). |
||
|
|
|||||||||
|
|
|
h |
i |
|
2h2 |
i |
i+1 |
|
|
|
|
|
|
|
|
|
|
|
||
Очевидно, |
что при подстановке x = xi или |
x = xi+1 или x = xi−1 получается |
||||||||
тождество.
Кусочно-кубическая интерполяция.
f (x) ≈ f |
i |
+ |
fi+1 |
− fi |
(x − x ) + |
fi+1 − 2 fi |
+ fi−1 |
(x − x |
)(x − x |
) |
||||
|
|
|
|
|||||||||||
|
|
|
h |
|
i |
2h2 |
|
|
i |
i+1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
+ |
fi+2 −3 fi+1 +3 fi − fi−1 |
(x − x |
)(x − x |
)(x − x |
) |
|
|
|||||||
|
|
|
||||||||||||
|
|
|
|
6h3 |
|
|
|
i−1 |
i |
|
i+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
38
Нетрудно убедиться, что при fi−1 , fi , fi+1 , fi+2 в последних двух форму-
лах стоят биномиальные коэффициенты.
Более высокие степени ИП для КИ, как правило, не используют.
Узлы интерполяции при кусочной интерполяции берутся вблизи интересующего нас узла xi . (Рис. 5.1)
Рис. 5.1 Узлы интерполяции при кусочной интерполяции
Вообще, нетрудно проследить идейное сходство идеи кусочной интерполяции функции и метода среднеквадратичного приближения (метода наименьших квадратов), который был рассмотрен ранее.
Возможные обобщения приближения функций с помощью интерполяции.
По аналогии с ИП можно искать приближение таб-
лично заданной функции в виде обобщенного ИП:
Pn (x)= a0φ0 (x)+ a1φ1(x)+... + anφn (x)
по системе линейно независимых функций {φk (x):k = 0,1,...,n}.
Исходя из условий интерполяции (совпадения значения полинома с табличными значениями функции), для неопределенных коэффициентов {ai } по-
лучим систему линейных уравнений:
a0φ0 (xi )+ a1φ1(xi )+... + anφn (xi )= fi , i = 0,1,..., n .
Для существования и единственности решения необходимо, чтобы детерминант удовлетворял условию
φ0 (x0 ) φ1(x0 )
=φ0 (x1 ) φ1(x1 )
... ...
φ0 (xn ) φ1(xn )
... φn (x0 ) |
|
|
|
||
... |
φn (x1 ) |
≠ 0 |
... |
... |
|
... |
φn (xn ) |
|
Например, периодическую функцию может оказаться удобно приближать
в |
виде |
полинома |
по |
системе |
функций |
{φk (x)=1, |
sin(kx), |
cos(kx), |
k =1,2,...,m; |
(2m +1) = n} |
- это тригоно- |
39
метрическая интерполяция. Часто используется, если функция разложима в ряд Фурье.
Если в табличных точках заданы не только значения функции, но и ее производные, то для приближения функции используются полиномы Эрмита. Для построения используется следующие условия:
•В табличных точках полином принимает заданные значения;
•Производные от полинома также принимают заданные значения.
Втаких случаях полиномы Эрмита обеспечивают лучшее приближение сравнительно с обычной интерполяцией.
Интерполяция кубическими сплайнами.
В отличие от кусочно-кубической интерполяции, здесь при переходе от одного участка интерполяции к другому не претерпевают разрыва не только первые производные, но и вторые. Это значит, что сплайновая интерполяция обеспечивает сквозное (на всем участке интерполирования) гладкое приближение к функции f (x) в виде полиномов третьей степени.
Строятся они следующим образом. На каждом отрезке [xk ; xk +1 ] ищется полином третьей степени P3k (x)= ak + bk x + ck x2 + dk x3 со своими коэффициен-
тами. Потребуем, чтобы в табличных точках полином принимал заданные значения:
.
Кроме того, необходимо следующее условие:
P |
(k )′ |
(x |
k |
|
)= P(k −1)′(x |
k |
) |
|
|
|
||||||||
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||
|
|
″ |
(x |
|
|
)= P |
″ |
(x |
|
) |
|
|
||||||
P |
(k ) |
|
k |
(k −1) |
k |
|
|
|||||||||||
|
3 ′ |
(x |
|
|
|
3 |
′ |
|
|
|
) |
|
||||||
P |
(k ) |
k |
+1 |
)= P(k +1) (x |
k |
+1 |
|
|||||||||||
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|||||||
P |
(k )″(x |
k |
+1 |
)= |
P(k +1)″(x |
k +1 |
) |
|||||||||||
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|||||||
В итоге получаем замкнутую систему для 4n неопределенных коэффициентов, которая решается относительно просто.
Отметим еще задачу обратной интерполяции.
40

Пусть необходимо определить, при каком значении x функция |
f (x) при- |
||||
нимает заданное значение. Учитывая, что при заданной таблице |
|
||||
|
|
|
|
|
|
x |
x0 |
x1 |
… |
|
xn |
f (x) |
f0 |
f1 |
… |
|
fn |
|
|
|
|
|
|
с формальной точки зрения безразлично, что считать функцией и что аргументом, в этом случае представляется удобным приближать с помощью ИП зависимость x = x(f ). Это и есть обратная интерполяция. ИП в форме Лагран-
жа и в форме Ньютона выписывается стандартным образом.
Численное дифференцирование.
Итак, пусть в точках xi , i = 0,1,..., n известны значения функции
f (x) :{fi ,i = 0,1,..., n}.
Простейший способ построения численного дифференцирования состоит в следующем. По табличным данным приближаем функцию ИП.
Дифференцируя полином нужное число раз, получаем требуемую форму-
лу.
Например, f (x) = Pn (x)+ Rn (x),
∂k f |
∂k P (x) |
|
|
n |
|
∂xk ≈ |
|
. |
∂xk |
||
Погрешность формулы характеризуется k -той производной от ошибки
интерполяции: ∂k Rn (x).
∂xk
Замечание.
Анализ погрешности формул численного дифференцирования, опирающийся на оценку остаточного члена затруднен тем, что его выражение, как следует из его вывода (Лекция 3)
Rn (x)= f(n++1(x)′) ωn+1(x),
n 1 !
n
где ωn+1(x)= (x − x0 )(x − x1 )...(x − xn )= ∏(x − xi )
i=0
содержит неявную зависимость x′ = x′(x) [x0 ; xn ] .
41

Поэтому будем иначе анализировать точность формул численного дифференцирования.
Примеры.
Приближение производных функции f (x) в окрестности табличной точки
x = xi . Пусть xi = x0 +ih , h = const .
Приближение полиномом первой степени
f (x) ≈ P1(x)= fi + fi+1h− fi (x − xi )
совпадает с функцией в точках x = xi и x = xi+1 .
∂f |
|
|
≈ |
∂P1(x) |
= |
fi+1 − fi |
|
||||||
|
|
|
|
|||
∂x |
|
x=x |
|
∂x |
|
h |
|
|
|
||||
|
|
i |
|
|
|
|
Используя кусочно-линейную интерполяцию, можно было бы записать и так:
f (x) ≈ P1(x)= fi + fi −hfi−1 (x − xi )
совпадает с функцией в точках x = xi−1 и x = xi .
∂f |
|
|
|
∂ |
|
(x) |
|
fi − fi−1 |
. |
|
|
≈ |
P1 |
= |
|||||
|
|
|
|
|
|
||||
∂x |
|
x=x |
|
|
∂x |
|
h |
||
|
|
|
|||||||
|
|
i |
|
|
|
|
|
|
|
Мы получили простейшие приближенные формулы для первой производной от функции, заданной таблично: правое и левое разностные отношения. Их можно было бы написать и сразу, не привлекая интерполяцию в качестве промежуточного этапа. Ясно также, что для получения приближенных формул для второй производной линейного приближения функции недостаточно.
Приблизим f (x) в рассматриваемой окрестности точки полиномом второй степени:
f (x) ≈ P |
(x)= f |
i |
+ |
fi+1 |
− fi−1 |
(x − x )+ |
fi+1 − 2 fi |
+ fi−1 |
(x − x )2 |
|
|
|
|
||||||
2 |
|
|
|
2h |
i |
2h2 |
|
i |
|
|
|
|
|
|
|
|
|
(совпадает с табличными значениями функции в т. x = xi−1 , x = xi , x = xi+1 ),
отсюда:
∂f |
≈ |
fi+1 − fi−1 |
+ |
fi+1 − 2 fi + fi−1 |
, здесь приближение зависит от x . |
|
∂x |
2h |
h2 |
||||
|
|
|
При x = xi :
42
∂f |
|
|
≈ |
fi+1 − fi−1 |
. |
|
|||||
∂x |
|
x=x |
|
2h |
|
|
|
i |
|
|
|
Получено так называемое центральное разностное отношение.
Дифференцируя 2 раза, получим
∂2 f |
≈ |
f |
i+1 |
− 2 f |
i |
+ f |
i−1 |
∂x2 |
|
|
h2 |
|
|
||
x=x |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
Получение выражений для производных путем разложения функции в ряд
Тейлора. Погрешность формул численного дифференцирования. |
|
|||||||||||||||||||||||||||
Разложим функцию f (x) |
в ряд Тейлора в окрестности т. x = xi , |
предпола- |
||||||||||||||||||||||||||
гая существование соответствующих производных. |
|
|
||||||||||||||||||||||||||
Так как xi+1 − xi = h , xi−1 − xi = −h , получим |
|
|
||||||||||||||||||||||||||
|
fi+1 = fi + fi′ h + |
|
1 |
fi′′ h2 + |
1 |
|
fi′′′ h3 + |
1 |
|
fi′′′′ h4 + Ο(h5 ) |
(1) |
|
||||||||||||||||
2! |
3! |
|
4! |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
fi−1 = fi − fi′ h + |
|
1 |
fi′′ h2 − |
|
1 |
|
fi′′′ h3 + |
|
1 |
|
fi′′′′ h4 + Ο(h5 ) |
(2) |
|
||||||||||||||
2! |
|
3! |
|
|
4! |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из формулы (1) следует: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
fi′ = |
fi+1 − fi |
+ |
|
1 |
|
M |
2 h, где M 2 = fi′′ . |
|
|
|
|
|
|
|
|
||||||||||||
h |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
fi′ = |
fi+1 − fi |
|
|
+ Ο(h). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из формулы (2) следует: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
fi′ = |
fi − fi−1 |
|
+ |
1 |
|
M |
2 h = |
fi − fi−1 |
+ Ο(h) ; |
|
|
|
|
|
|
||||||||||||
h |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Эти формулы аппроксимируют, т.е. приближают производную |
fi′ в том |
|||||||||||||||||||||||||||
смысле, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
fi′ − |
fi+1 − fi |
|
→0 и |
|
fi′ − |
fi − fi−1 |
|
|
→0 |
|
|
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
h |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
h → 0 |
|
|
|
|
h |
|
|
|
h → 0 |
|
|
||||||||||||
Причем порядок стремления к нулю есть O(h), т.е. пропорционально пер-
вой степени величины h . Это первый порядок аппроксимации производной разностным отношением.
Вычитая из формулы (1) формулу (2), получим
43

fi′ = |
fi+1 − fi−1 |
− |
1 |
|
fi′′h2 + Ο(h4 ), |
||||
|
|
6 |
|
||||||
|
|
2h |
|
|
|
||||
|
|
|
fi+1 − fi−1 |
|
→0 как C h2 . |
||||
т.е. |
fi |
′ − |
|
||||||
|
|||||||||
|
|
|
2h |
|
|
|
h → 0 |
||
Это аппроксимация второго порядка (малости по h ). Складывая формулы (1) и (2) , получим для второй производной:
fi′′ = |
fi+1 − 2 fi + fi−1 |
+ Ο(h2 ). |
|
h2 |
|||
|
|
Это аппроксимация второй производной второго порядка малости по h . Итак, мы получили три разностных отношения для первой производной одно второго порядка аппроксимации и два первого порядка аппроксимации; и одно выражение для второй производной - второго порядка аппроксимации. Используя разложение функции в ряд Тейлора, мы не будем получать
производных более высокого порядка.
Неустойчивость формул численного дифференцирования. Рассмотрим влияние погрешности входных данных на результат вычисле-
ния производных по формулам ЧД.
|
|
|
|
|
|
~ |
|
Пусть в точках {xi ,i = 0,1,...,n} заданы значения функции {fi }, которые отли- |
|||||||
чаются от точных значений |
~ |
|
|||||
fi = f (xi ),т.е. fi = fi ± δi , |
|
||||||
где δi |
- погрешность входных данных. Величина δ = max δi |
обычно бывает |
|||||
|
|
|
|
|
|
i |
|
известна. Пусть в точке x = xi |
нужно приближенно вычислить |
′ |
|||||
f (x). |
|||||||
∂f |
|
~ |
~ |
|
|
|
|
|
≈ |
fi+1 |
− fi |
. |
|
|
|
|
|
|
|
|
|
||
∂x |
x=x |
|
h |
|
|
||
|
i |
|
|
|
|
|
|
Погрешность формулы
|
|
|
∂f |
|
~ |
|
|
|
~ |
|
|
|
|
∂f |
|
f |
|
|
− f |
|
|
|
|
f |
|
− f |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
= |
|
− |
|
f |
i+1 |
− f |
i |
|
= |
− |
i+1 |
i |
|
i+1 |
i |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
− |
|
|||||||||||||||
|
∂x |
|
|
|
|
|
|
|
∂x |
|
|
h |
|
|
h |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
∂f |
|
fi+1 − fi |
|
|
|
|
|
|
|
|
|
|
|
fi |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
≤ |
− |
|
+ |
|
|
fi+1 − fi+1 |
+ |
− fi |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
∂x |
|
|
|
h |
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
≤ |
M |
2 |
|
h + |
|
2δ |
= Φ(h) , гдеM 2 |
= |
max |
|
|
′′ |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
[xi ;xi+1 |
] |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
~ |
|
|
~ |
|
|
||
|
|
|
|||||
f |
i+1 |
− f |
|
≤ |
|||
|
|
|
i |
||||
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
методическая  неустранимая ошибка погрешность
неустранимая ошибка погрешность
44
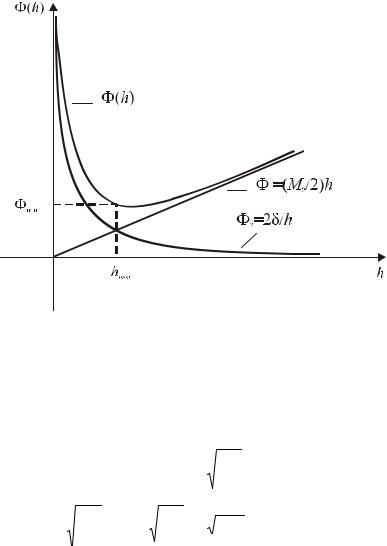
Рассмотрим график функции Φ(h) ( Рис. 5.2). |
Рис.5.2 График функцииΦ(h)
Ясно, что при h → 0 , например, h δ, неустранимая погрешность Ο(1).
Нет аппроксимации. Можно сколь угодно исказить вычисляемый по формуле результат.
h |
: |
|
dΦ(h) |
= |
M 2 |
− |
2δ |
= 0 |
|
h |
= 2 |
δ |
. |
|||||||||
|
|
|
|
|
|
|
||||||||||||||||
опт |
|
|
dh |
|
2 h2 |
|
|
|
|
|
опт |
|
M 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Тогда |
Φ(h |
) = |
M 2 |
2 |
|
δ |
+ 2δ |
1 |
|
M 2 |
|
= 2 M |
2 |
δ . |
||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
опт |
2 |
|
|
|
M 2 |
2 |
|
δ |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
M 2 ~ 1, |
|
|
|
δ ~ 0.01 |
|
|
|
~ 0.1. |
|
|
|
|
||||||||||
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пусть задана функция y = sin(x) |
на x [0;π]. |
|
|
|||||||||||||||||||
Возьмем значение функции в 10 точках с погрешностью входных данных
σ = 0.01 , т.е. ~pi = pi +σ rand(1,1) .
Построим ИП, например, используя функцию MATLAB y=polyval( ~p, x ), где ~p - коэффициенты полинома в точках x .
Используя функцию MATLAB k = polyder( ~p) , найдем коэффициенты поли-
нома, получающиеся при дифференцировании данного.
45
Погрешность вычисления y′ |
|
|
|
|
|
|
|
|
|
π |
, |
π |
, |
π |
|
, |
|
|
|
|
|
|
|
|||||||||||||||||||
в точках |
|
6 |
4 |
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Φ(h)= |
|
M |
n+1 |
hn+1 |
+ 2 |
σ |
≈ |
2 |
|
1 |
|
|
π |
11 |
|
|
|
0.01 |
|
|
1 |
|
|
|
|
≈ 0.2 . |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ 2 |
|
|
|
|
|
= |
|
|
|
|
|
+ 0.2 |
|||||||||||||||||||
|
n |
+1 |
h |
2 |
10 |
|
0.1 |
|
|
310 |
|
20 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Количество арифметических операций (при вычислении значений ИП). |
||||||||||||||||||||||||||||||||||||||||||
Пусть надо вычислить |
P (x) = a |
n |
xn |
+ a |
n−1 |
xn−1 |
+... + a x + a |
0 |
|
в т. x . Можно вы- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||
числять различными способами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
вычислить a1x и сложить с a0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
вычислить a2 x2 |
|
и сложить с полученным результатом и т.д. |
||||||||||||||||||||||||||||||||||||||||
на |
j -ом шаге вычисляется a j x j |
и складывается с уже вычисленной сум- |
||||||||||||||||||||||||||||||||||||||||
мой a |
0 |
+ a x +... + a |
j−1 |
x j−1 . Вычисление a |
j |
x j |
|
требует j операций умножения. |
||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Т.о. для вычисления P (x) |
требуется 1+ 2 +... + n = |
n(n +1) |
операций умноже- |
|||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ния и n операций сложения. Количество действий |
Φ = |
n(n +1) |
+ n . |
|||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ясно, что количество действий может быть уменьшено. Можно последо-
вательно вычислять и запоминать x2 , x3 ,..., xn , тогда потребуется (n −1) опера-
ция умножения. Далее вычисляются a j x j - n операций умножения и n опера-
ций сложения. Количество действий Φ2 = (2n −1) + n . Уже при n > 2 Φ2 < Φ1 .
Можно еще эффективнее:
Pn (x) = (...(an x + an−1)x + an−2 )x +...)x + a0 .
Для вычисления каждой скобки 1 операция умножения и 1 операция сложения. Количество действий Φ3 = n + n .
Φ3 < Φ2 < Φ1 при n > 2 .
Количество арифметических действий - важнейшая характеристика численного метода.
Часто оценивают не количество, а просто порядок количества арифметических операций.
46
В рассматриваемых примерах |
Φ = O(n2 ); |
Φ |
,Φ |
3 |
= O(n) , где n - степень |
|||
|
|
|
|
1 |
2 |
|
|
|
многочлена. |
|
|
|
|
|
|
||
Φ = |
1 |
n2 |
+O(n2 ) |
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Φ2 = 3n +O(n)
Φ3 = 2n
Заметим, что Pn (x) определяется величинами a0 ,a1,..., an и x .
Поэтому в общем случае для вычисления Pn (x) требуется не менее n дей-
ствий – оценка снизу.
Т.о. Φ2 ,Φ3 методы являются оптимальными по порядку, т.к. Φ2 ,Φ3 = O(n) и
для каждого метода Φ ≥ n .
Методы с числом действий O(n) называются экономичными.
47

Лекция 6. Численное интегрирование.
b
Определенный интеграл ∫ f (x)dx возможно точно найти по формуле Нью-
a
b
тона - Лейбница ∫ f (x)dx = F (a) − F (b) только в тех редких случаях, когда инте-
a
грал является табличным.
Рассмотрим способы приближенного вычисления определенных интегралов. Формулы для приближенного вычисления интеграла по таблице значений подынтегральной функции называют квадратурными формулами.
Общая схема простейших квадратурных формул.
Геометрический смысл определенного интеграла ∫b f (x)dx - площадь.
a
Для приближенного вычисления этой площади разобьем отрезок [a,b] на некоторое число N отрезков, так чтобы a = x0 < x1 <... < xn = b .
Определение.
xn - назовем узлами интегрирования, hn = xn+1 − xn - шагами интегрирования, fn = f (xn ) .
В частном случае hn = const;h = b N− a .
Затем заменим функцию y = f (x) кусочно-интерполяционным многочле-
ном:
Pk (x) = Pk (x, f , x0 , x1,..., xn ) .
Функция Pk (x) на каждом отрезке [xn , xn+1] есть многочлен степени не вы-
ше k . Он выбирается по точкам, ближайшим к данному отрезку x [xn , xn+1] .
Напомним формулы кусочной интерполяции (Из лекции 5). Кусочная интерполяция нулевого порядка
48

f (x) ≈ fn или f (x) ≈ fn+1 , или f (x) ≈ fn+12 ≡ f (xn + h2n ) (если есть значение функции в точке n + 12 ).
Кусочно-квадратичная интерполяция
f (x) ≈ fn + |
fn+1 − fn |
(x − xn ) (по узлам x = xn и x = xn+1 ) |
||||
|
|
|||||
|
|
h |
|
|
||
Кусочно-квадратичная интерполяция |
|
|||||
f (x) ≈ fn + |
|
fn+1 − fn |
(x − xn ) + |
fn+1 − 2 fn + fn−1 |
(x − xn )(x − xn+1) |
|
|
|
2h2 |
||||
|
|
h |
|
|||
(используется еще одна точка x = xn−1, xn , xn+1 ).
Таким образом, у нас есть интерполяционный полином степени не выше
k .
Для приближенного вычисления интеграла можно воспользоваться формулой:
b |
N∑−1Pk (x)dx ( ) |
y = ∫ f (x)dx ≈ |
|
a |
n=0 |
Определение.
Квадратурные формулы ( ) с равноотстоящими узлами называются фор-
мулами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ньютона - Котеса порядка k |
с N +1 узлами, где k – порядок интерполя- |
|||||||||||||
ции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формула прямоугольников. |
|||||||
Пусть k = 0, f = P0 (x) . |
|
|
|
|
||||||||||
Считая hn |
малым, если есть значение fn+ |
1 , |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
J = N∑−1hn fn+1 |
при hn = h = const |
|
|
|
(1) |
|||||||||
n=0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
N −1 |
|
|
|
|
|
|
M n+1 |
|
|
|
|
|
|
|
J = h∑ fn+ |
|
|
|
Rn (x) |
|
|
|
|
+1(x) |
|
|
|
||
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
≤ |
|
|
|
ωn |
|
|
|
|||
|
|
|
(n +1)! |
|
||||||||||
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
|||||||||
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49

если нет f |
1 , |
то J = hN∑−1 fn ≈hN∑−1 fn+1 , но в этом случае точность формулы |
|
n+ |
2 |
n=0 |
n=0 |
ухудшается. Геометрическая интерпретация на Рис. 6.1
Рис. 6.1 Геометрическая интерпретация формулы прямоугольников
Формула трапеции. На элементарном отрезке x [xn , xn+1]
P1(x) = fn + fn+1 − fn (x − xn ) xn+1 − xn
xn+1 |
|
|
1 |
|
f |
|
− f |
|
|
xn+1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Jn = ∫P1(x)dx = |
fn (xn+1 |
− xn ) + |
|
n+1 |
n |
(x − xn )2 |
= |
hn ( f |
+ fn+1) . |
|||||
|
|
|
|
|
|
xn |
2 |
|||||||
xn |
|
|
2 xn+1 − xn |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(площадь трапеции Рис. 6.2).
Рис. 6.2 Геометрическая интерпретация формулы трапеции
50

J= 1 N∑−1hn ( fn + fn+1) . В случае постоянного шага трапеции:
2 n=0
|
h |
N −1 |
h |
|
|
(2) |
J = |
|
∑( fn + fn+1) = |
|
[ f0 |
+ 2 f1 +... + 2 fN −1 + fN ] |
|
2 |
2 |
|||||
|
|
n=0 |
|
|
|
|
Формула Симпсона. (Соответствует интерполяционному полиному второй степени Pn (x) ).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fn+1 |
− 2 f |
1 + fn |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
fn+1 − fn |
|
xn+1 + xn |
|
|
|
|
|
n+ |
|
|
|
[x − |
xn+1 + xn |
]2 |
||||||||||
|
f (x) ≈ P (x) |
= f |
1 |
+ |
[x − |
] + |
|
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
hn |
2 |
|
|
|
|
2(hn )2 |
|
|
|
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
n+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
xn+1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Jn = ∫P2 (x)dx = |
|
hn |
( fn |
+ 4 fn+1 + fn+1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Суммируя Jn |
по всем отрезкам, получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
J n = |
1 |
N∑−1hn ( fn |
+ 4 f |
|
|
1 |
|
+ fn+1 ) =[если hn = const] = |
1 |
hN∑−1( fn |
+ 4 f |
1 |
|
+ fn+1 ) = |
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
6 n=0 |
|
|
|
|
|
|
n+ |
|
|
|
|
|
|
|
|
|
|
|
6 n=0 |
|
|
|
n+ |
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
(3) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
h( f0 + 4 f 1 |
+ 2 f1 + 4 f 3 |
+ ... + 2 f N −1 |
+ 4 f |
1 + f N ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Замечание.
Если использовать локальную формулу по паре элементарных отрезков,
|
|
|
xn+1 |
|
1 |
|
|||
|
|
|
|
|
~ |
|
|
||
Jn′ = |
|
∫P2 |
(x)dx = |
|
hn ( fn−1 + 4 fn + fn+1) , тогда |
||||
3 |
|||||||||
|
|
|
xn−1 |
|
|
|
|
||
J |
′ |
= |
1 |
|
h( f |
|
|
|
′ |
|
|
|
|
|
|||||
|
3 |
|
0 + 4 f1 + 2 f2 + 4 f3 +... + 2 f N −2 + 4 fN −1 + fN ) (3 ) |
||||||
|
|
|
|
|
|
|
|
|
|
Интеграл J ′ |
записывается без дробных индексов. |
||||||||
Здесь |
~ |
(x) |
- интерполяционный полином на отрезке [xn−1, xn+1] по точкам |
||||||
P2 |
|||||||||
xn−1, xn , xn+1 .
(Число пар на отрезке [a,b] должно быть четным, т.е. N – четное.)
Погрешность квадратурных формул.
Оценим погрешность квадратурных формул аналогично оценке погрешности формул численного дифференцирования, используя разложение в ряд Тейлора.
51
Еще одним способом оценки является оценка остаточного члена интерполяционной формулы.
|
|
|
|
xn+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть Jn = |
∫ f (x)dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разложим f (x) |
в окрестности точки |
x |
1 в ряд Тейлора. |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = f |
|
1 + f ′ |
1 |
(x − x |
1 ) + |
1 |
|
f ′′ |
1 (x − x |
|
1 )2 |
+... + R(x − x |
|
1 ) |
(**) |
|
|
||||||||||
|
2! |
|
|
|
|
||||||||||||||||||||||
n+ |
|
|
n+ |
|
n+ |
|
|
|
n+ |
|
|
n+ |
|
|
|
|
n+ |
|
|
|
|
|
|
||||
2 |
|
2 |
2 |
|
|
2 |
|
2 |
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- остаточный член формулы Тейлора (зависит от числа произ- |
||||||||||||||||||||||||
R x − xn+ |
1 |
||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
водных функции f (x) ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Вычисляя интеграл от этой суммы, получим: |
|
|
|
|
|
|
|
||||||||||||||||||||
xn+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn+1 |
|
|
|
|
|
|
|
||
Jn = ∫ f (x)dx = fn+1 hn + A hn |
2 |
|
3 |
+... + |
|
∫ |
|
|
|
(4) |
|
|
|||||||||||||||
|
+ |
B hn |
|
R x − xn+ |
1 |
dx |
|
|
|||||||||||||||||||
xn |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
xn |
|
2 |
|
|
|
|
|||
Здесь коэффициенты A, B,… зависят от производных f ′ |
1 |
, f ′′ |
1 и т.д. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n+ |
2 |
n+ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Заметим, что каждая из рассмотренных формул (прямоугольников, трапеций, Симпсона) в пределах элементарного отрезка [xn , xn+1] может быть пред-
ставлена в виде:
~ |
|
+ qfn+1] |
(5) |
Jn = h[rfn + sf |
1 |
||
n+ |
2 |
|
|
|
|
|
с коэффициентами r, s,q .
Например, для формулы прямоугольников:
~ |
|
|
f |
1 , т.е. r = q = 0, s =1 |
; |
|
|
|
|
|
|
|||
Jn = h |
|
|
|
|
|
|
||||||||
|
|
|
n+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
для формулы трапеций: |
|
|
|
|
|
|
|
|||||||
~ |
|
1 |
h[ fn + fn+1] , т.е. r = q = |
1 |
|
; |
|
|
|
|||||
Jn = |
|
|
, s = 0 |
|
|
|
||||||||
2 |
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
для формулы Симпсона: |
|
|
|
|
|
|
|
|||||||
~ |
|
1 |
|
|
|
1 + fn+1] , т.е. |
|
|
1 |
|
4 |
. |
||
Jn = |
|
|
h[ fn + 4 f |
r = q = |
|
|
, s = |
|
||||||
|
6 |
6 |
6 |
|||||||||||
|
|
|
|
n+ |
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52

Заменяя в (5) каждое из значений fn , fn+1 по формуле Тейлора,
fn+1 = fn+12 + hn fn′+12 + 21!( h2n )2 fn′′+12 +...
fn = fn+12 − h2n fn′+12 + 21!( h2n )2 fn′′+12 +...,
получим представление Jn , аналогичное(4) .
~ |
|
2 |
3 |
|
~ |
(6) |
|
Jn = fn+ |
1 |
hn + A1 hn |
+ B1 hn |
+ |
... + R |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравнив формулы |
(4) и (6) |
для |
Jn и |
~ |
|||
Jn ,обнаружим, что кроме первого |
|||||||
слагаемого, совпадают еще и (p −1) слагаемых, т.е. A = A1,B = B1,...
Разность несовпадающих слагаемых будет характеризовать ошибку квадратурной формулы.
На интервале [xn , xn+1]
~ |
|
≤ D max |
|
f |
( p) |
|
hn |
p+1 |
(7) |
|
|
|
|||||||
Jn − Jn |
|
|
|
|
|
||||
|
|
[xn ,xn+1 ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D =const , если обозначить μ |
p |
= max |
f ( p) |
,h = max h , то |
||||||||
|
|
|
|
|
|
|
|
[a,b] |
|
n |
n |
|
= |
|
~ |
− J |
|
≤ D (b −a) μp h |
p |
(8) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
J |
|
|
|
|
|
|
|||||
Степень p - точность квадратурной формулы.
Рассмотрим конкретные разложения:
f (x) = f |
1 + f ′ |
1 |
(x − x |
|
|
|
1 ) + |
|
1 |
|
|
|
f ′′ |
1 |
(x − x |
|
1 )2 |
+... + R(x − x |
|
1 ) |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
2! |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n+ |
|
|
|
|
n+ |
|
|
|
|
|
|
|
|
|
n+ |
|
|
|
|
|
|
|
|
|
n+ |
|
|
|
|
|
n+ |
|
|
|
|
|
|
|
|
|
n+ |
|
|
|
|
|
|
|
||||||||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
xn+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
n |
+ |
1 |
|
|
|
|
|
|
|
|
x |
n |
+ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Jn = ∫ f (x)dx = f |
|
|
|
1 hn + |
|
|
|
|
f ′ |
1 (x |
− x |
|
1 ) |
2 |
|
1 + |
|
|
f ′′ |
1 (x − x |
1 )3 |
|
|
1 +... |
||||||||||||||||||||||||||||||||||||||||
n+ |
2 |
|
|
|
xn |
3! |
|
xn |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
xn |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
n+ |
2 |
|
|
|
n+ |
2 |
|
|
|
|
n+ |
2 |
|
|
n+ |
2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
′′ |
|
hn |
|
|
|
3 |
+ |
|
2 |
|
f |
(4) |
|
1 |
|
hn |
|
|
5 |
+... |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Jn = fn+ |
|
hn + |
3! |
fn+ |
1 |
|
2 |
|
|
|
5! |
|
|
n+2 ( |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. Формула прямоугольников |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
~ |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jn = h f |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
n+ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
1 |
|
|
|
′′ |
|
|
|
|
|
|
|
3 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
n = |
Jn − Jn |
|
= |
|
|
|
|
|
|
|
1 |
|
|
hn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
24 |
fn+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
~ |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, h = max hn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
= |
J − J |
|
≤ |
|
|
|
|
(b |
− a) M 2 h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
53
2. Формула трапеций
~ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 hn + |
1 |
′′ |
3 |
+..., |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Jn = 2 hn[ fn + fn+1 |
] = fn+ |
8 |
fn+ |
1 |
hn |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
~ |
|
|
|
1 |
|
′′ |
|
3 |
, |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
n = |
Jn − Jn |
= |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
12 |
|
fn+ |
|
hn |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
J − J |
≤ |
|
|
|
(b − a) |
M 2 h |
|
|
|
|
|
|
|
|
||||||||||||||
12 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. Формула Симпсона |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Для полуцелых узлов |
|
≤ |
1 |
|
(b − a) M 4 h4 . |
||||||||||||||||||||||||
2880 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для целых узлов |
|
≤ |
1 |
|
(b − a) M 4 h4 . |
|
|
||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
130 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Замечание.
Для оценки необходима гладкость подынтегральной функции.
Если в 3. нет f (4) , то оценка ухудшается на порядок.
Контроль над точностью вычисления интеграла. Автоматический выбор шагов.
Если известны оценки соответствующих производных,
= |
|
~ |
|
|
≤ D (b − a) M p h |
p |
, |
|||
|
|
|||||||||
|
J − J |
|
|
|
||||||
M p = max |
|
f ( p) |
|
, |
|
|
||||
|
|
|
|
|||||||
|
|
[a,b] |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
то можно, регулируя величину шага h = const , получить требуемую по-
грешность вычисления интеграла ε: D(b − a)M ph p ≤ ε.
Однако обычно оценок производных мы не знаем. Тогда контроль над точностью вычисляемого интеграла можно организовать, проводя вычисления на последовательно сгущающейся сетке узлов интегрирования.
Пусть h = const , |
J (h) - вычисленное с шагом h приближение к J . Если те- |
||||||||||
|
|
|
|
|
|
h |
|
|
|
||
|
|
|
|
|
|
|
|
h |
|
||
перь вычислить |
J 2 |
с шагом |
, то можно сделать приближенную оценку |
||||||||
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
h |
|
|
|
J ( |
h |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
J ( 2 ) − J |
|
≈ |
|
2 ) − J (h) |
. |
|
|
|||
54

Далее можно последовательно вдвое уменьшать шаг до тех пор, пока не выполнится условие:
h |
|
|
|
||
|
|
|
(h) |
|
|
2 |
< ε |
||||
J |
− J |
||||
|
|
|
|
|
|
Автоматический выбор шагов.
Замечание.
Представленную выше оценку можно выполнять для каждого интервала hn = xn+1 − xn посредством последовательного уменьшения (или увеличения!)
вдвое начальной длины, так чтобы
|
~ |
|
|
J (h) − J |
( |
h |
) |
|
h |
. |
|||
|
|
|
|
|
|
||||||||
|
J |
− Jn |
≈ |
2 |
|
< ε |
n |
||||||
|
|
(b − a) |
|||||||||||
|
|
|
|
|
hn |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||||
Тогда ∑ε |
|
|
|
= ε, ошибка на отрезке [a,b] не превосходит ε , а шаг из- |
|||||||||
(b − a) |
|||||||||||||
|
|
|
n |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
меняется в соответствии с изменениями функции: если функция резко изменяется, то шаг уменьшается, если функция изменяется медленно, то шаг увеличивается.
Устойчивость квадратурных формул.
Устойчивость численного интегрирования следует из основной формулы
~ |
= ∑Ci fi . ( Ci - постоянные коэффициенты).мЯсно, что ∑Ci = b − a . |
|
J |
||
|
i |
i |
(Численное интегрирование дает точный результат при f = const , в том
числе при f =1 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Если теперь |
fi = fi ± δi , то |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
~ |
|
= |
|
|
|
|
|
~ |
|
= |
|
|
|
|
|
|
~ |
|
≤ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
J − J |
|
J −∑Ci fi |
|
(J − ∑Ci fi ) + (∑Ci fi − ∑Ci fi ) |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
i |
i |
|
i |
|
|
||
≤ |
|
J − ∑Ci fi |
|
+ ∑Ci |
|
~ |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
fi − fi |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
i |
|
|
i |
|
|
|
|
|
|
~ |
|
|
|
|
||||||
|
|
|
J − ∑Ci fi |
|
- ошибка метода; ∑Ci |
|
|
- неустранимая погрешность, обу- |
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
fi − fi |
|
|||||||||||||||||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|||
словленная неточными входными данными.
55

∑ − ~ ≤ ∑ = − .
Ci fi fi δ Ci δ(b a)
i
Таким образом, неустранимая погрешность при вычислении по квадратурным формулам остается величиной ограниченной (и является порядка самих входных данных, если (b − a) 1 ).
Вычисление сходящихся несобственных интегралов.
b
1) ∫ f (x)dx , причем f (x) → ∞ при x → a .
a
∞
2) ∫ f (x)dx .
a
Рассмотрим интегралы вида 2).
|
|
|
|
0 |
1 |
|
|
|
1 |
|
dt |
f |
|
||
Вводим замену t = |
, dx = − |
, ∫ |
t |
|
dt . Таким образом, интеграл 2) сводит- |
||
x |
2 |
2 |
|
||||
|
|
t |
1 |
t |
|
|
|
a
ся к виду интеграла 1) Рассмотрим интегралы вида 1).
Непосредственное применение формул трапеций или Симпсона невозможно (т.к. в узле интегрирования x = a функция не определена). Ис-
пользование формулы прямоугольников возможно, но оценка точности теряет смысл, т.к. f ′ не определена.
Пример.
1
J = ∫cos(x) dx .
0  x
x
Подходящая замена переменной:
x = t2 ;dx = 2tdt = 2 xdt;
J = 2∫1 cos(t2 )dt
0
Далее можно проводить вычисления с требуемой точностью по любой квадратурной формуле.
Интегрирование по частям:
1 |
cos(x) |
|
|
1 |
1 |
|
|
|
|||||
J = ∫ |
dx = 2 |
x cos(x) |
+ 2∫ x sin(x)dx . |
|||
|
0 |
|||||
0 |
x |
|
0 |
|||
|
|
|
|
|||
56

Последний |
интеграл |
можно вычислить, но оценка |
погрешности равна |
|||
O(h) , т.к. |
′ |
не существует. |
|
|||
f (0) |
|
|||||
Если |
еще |
раз проинтегрировать по частям, то |
получится функция |
|||
f (x) C2[0,1] . |
|
|
|
|
||
Разложение на два интеграла: |
|
|||||
J = J1 + J2 |
|
|
|
|
||
J1 = δ |
cos(x) |
dx ; J2 = 1 |
cos(x) |
dx . |
|
|
|
|
|
||||
∫ |
x |
∫ |
x |
|
||
0 |
|
|
δ |
|
|
|
Второй интеграл J2 не содержит особенности и вычисляется по любой квадратурной формуле.
Первый интеграл J1 вычисляется аналитически с требуемой точностью,
при разложении cos(x) в ряд Тейлора:
δ 1 − |
x2 |
|
+ |
x4 |
+... |
+ |
(−1) |
m |
|
x2m |
|
1 2 |
5 |
|
1 2 |
9 |
|
|||||||||||||
2! |
|
4! |
|
(2m)! |
|
|
|
|||||||||||||||||||||||
J1 = ∫ |
|
|
|
|
|
|
|
|
|
dx = 2 δ − |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
δ2 |
+ |
δ2 |
+... |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
2! 5 |
4! 9 |
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... + (−1)m |
|
|
1 |
|
|
|
1 |
|
|
|
δ2m+ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 +... |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
(2m)! (2m + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
1 )! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При рассмотрении ограничимся первыми слагаемыми.
Оценка J1 (т.к. интеграл знакопеременен) не превосходит последнего при-
веденного в записи члена:
1 |
|
1 |
|
2m+ |
1 |
|
ε |
, J2 ≤ |
ε |
. |
|
|
|
|
|
|||
|
|
2 ≤ |
|
|
|
|
|
|||||||||||
|
|
|
|
|
δ |
|
|
|
|
|
|
|
||||||
|
(2m)! |
(2m + |
|
2 |
2 |
|
|
|
||||||||||
|
1 )! |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Один из параметров m,δ задаем, другой вычисляется из оценки. |
||||||||||||||||||
Замечание. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При |
δ ≤1 |
существенно ухудшается оценка |
погрешности квадратурной |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
формулы для J2 , т.к. |
|
M p |
|
|
f ( p) |
|
, в точке x = δ |
M p δ−( p+ |
|
) . |
||||||||
|
= max |
|
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
[δ,1] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Поэтому целесообразно задавать не слишком малое δ , например δ = 0,1, а
значение количества слагаемых m найти из оценки J1 ≤ 2ε .
57

Все m членов ряда часто найти сложно. В этом случае вычисляются дос-
тупные слагаемые, а из оценки J1 ≤ |
ε |
находится δ. |
|
|
|||
|
2 |
|
|
Пример. |
|
|
|
∞ |
|
|
b |
J = ∫e−x2 dx . Данный интеграл можно свести к интегралу ∫ f (x)dx . |
|||
0 |
|
|
a |
Сделаем иначе. |
|
|
|
A |
∞ |
||
J = J1 + J2 ; J1 = ∫e−x2 dx ; J2 = ∫e−x2 dx . |
|||
0 |
A |
||
J1 вычисляется стандартными методами. |
|||
Выберем величину |
A таким образом, чтобы J2 можно было пренебречь, |
||
т.е. J2 ≤ 2ε .
Например, при A >1
∞ |
∞ |
2 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
∫e−x |
dx ≤ ∫xe−x |
|
dx = |
|
|
e−A |
|
. |
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
||||||||
A |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Потребуем, чтобы |
|
1 |
e−A2 |
≤ |
ε |
, A ≥ |
|
ln ε |
|
. |
||||||
|
|
|
||||||||||||||
2 |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Замечание-пример.
f (x) = 2x , x [0,1] .
f (x) P1(x) (Формула трапеции).
Т.к. |
f (x) точно описывается через P1(x) в двух точках, |
1 |
1 |
∫ f (x)dx − ∫P1(x)dx ≡ 0 . f (x) = x2 , x [0,1] . f (x) P2 (x) (Формула Симпсона).
0 |
0 |
|
Т.к. |
f (x) точно описывается через P2 (x) в трех точках, |
|
1 |
1 |
|
∫ f (x)dx − ∫P2 (x)dx ≡ 0 . |
||
0 |
0 |
|
|
1 |
1 |
Равенство ∫x2dx − ∫P2 (x)dx ≡ 0 также верно, если табличные значения функ-
0 0
ции f (x) точны.
58
