
- •Лекция 1. Общие сведения по теории вероятностей.
- •Условные и безусловные вероятности.
- •1.5. Формула полной вероятности и формула Байеса
- •Понятие случайного события.
- •1) Вероятность достоверного события равна 1;
- •2) Вероятность невозможного события равна 0;
- •Вероятность случайного события заключена
- •1.2. Алгебра событий.
- •1.3. Зависимые и независимые события.
- •1.4. Основные формулы теории вероятностей.
- •1.5. Формула полной вероятности и формула Байеса
- •1.6. Частная теорема о повторении опытов.
- •2.1. Случайные величины и их законы распределения.
- •2.2. Функция распределения.
- •2 .3. Вероятность попадания случайной величины
- •2.4. Плотность распределения
- •2.5. Числовые характеристики случайной величины
- •2.6 Понятие о моментах случайной величины.
- •2.7. Основные свойства математического ожидания
- •Свойства математического ожидания:
- •Свойства дисперсии случайной величины:
- •Лекция 3. Основные законы распределения
- •3.1. Гипергеометрическое распределение
- •3.5. Закон равной вероятности
- •3.7. Закон распределения модуля разности
- •3.8. Композиция законов распределения
- •3.1.Гипергеометрическое распределение.
- •3.5. Закон равной вероятности.
- •3.7. Закон распределения модуля разности.
- •Статистики
- •4.1. Основные задачи математической статистики
- •4.2. Основные понятия и определения. Выборочного метода
- •4.3. Выборочные характеристики. Состоятельные,
- •Свойства выборочных средних и дисперсий.
- •Доверительный интервал. Доверительная вероятность.
- •Задача определения закона распределения случайной величины.
- •2. Задача проверки правдоподобия гипотез.
- •3.Задача нахождения неизвестных параметров распределения.
- •4.2. Основные понятия и определения. Выборочного метода.
- •Генеральная совокупность и выборка из нее.
- •4.3. Выборочные характеристики. Состоятельные, несмещенные и эффективные оценки характеристики.
- •4.5. Доверительный интервал. Доверительная вероятность.
- •5.1. Определение характеристик эмпирического
- •5.2. Сопоставление и проверка сходимости
- •Координаты характерных точек кривой
- •5.3. Сопоставление эмпирического распределения
- •5.4. Статистическая проверка гипотез.
- •5.5. Проверка гипотезы о законе распределения случайной
- •Критерий
- •Критерий 2
- •5.6. Проверка гипотезы равенства двух выборочных средних
- •5.7. Проверка гипотезы равенства двух выборочных
- •5.8. Проверка гипотезы равенства ряда дисперсий .
- •Критерий Бартлета.
- •Критерий Кохрана.
- •5.9. Проверка гипотезы равенства ряда средних.
- •5.10. Метод исключения грубых ошибок измерения
- •5.11. Выбор числа наблюдений
- •6.1.Закон больших чисел и центральная
- •6.2. Неравенство Чебышева.
- •Неравенство Чебышева.
- •6.3. Закон больших чисел (теорема Чебышева).
- •6.4 Теорема Бернулли.
- •7.2. Коэффициент корреляции и корреляционное отношение.
- •7.3. Корреляционный анализ
- •7.4 Выбор уравнения регрессии
- •7.5. Понятие о множественной корреляции
- •Лекция 8. Основы планирования
- •8.6.1. Метод крутого восхождения.
- •8.1. Основные определения.
- •«Черный ящик »
- •8.3. Полный факторный эксперимент.
- •8.3.1 Выбор интервалов варьирования факторов
- •8.3.2 Полный факторный эксперимент типа 2
- •Построение матрицы 2
- •8.3.3. Свойства полного факторного эксперимента типа 2 к
- •8.3.4. Полный факторный эксперимент
- •8.3.5 Анализ модели.
- •8.3.5.1. Проверка значимости коэффициентов модели.
- •Расчет дисперсии опытов и оценка их однородности
- •Расчет дисперсий параметра оптимизации и коэффициентов регрессии
- •Проверка значимости коэффициентов регрессии
- •8.3.5.2. Проверка адекватности модели
- •8.4. Дробный факторный эксперимент.
- •8.4.1.Минимизация числа опытов.
- •Дробная реплика
- •8.4.3. Выбор полуреплик. Генерирующие соотношения и определяющие контрасты
- •8.4.4.Выбор 1/4-реплик. Обобщающий
- •8.6. Оптимизация функции отклика.
- •8.6.1. Метод крутого восхождения.
- •6.6.2. Методика расчета крутого восхождения
- •6.7. Принятие решений после построения модели процесса
- •8.5 Рандомизация опытов.
- •8.6 Оптимизация функции отклика
- •8.6.1. Метод крутого восхождения. Движение по градиенту
- •8.6.2. Методика расчета крутого восхождения
- •8.7.Принятие решений после построения
- •9.1. Статистический анализ точности обработки.
- •9.3. Статистический анализ посредством малых выборок.
- •9.4. Статистический анализ с помощью точечных
- •9.4.1. Карта средних значений (карта « »)
- •9.4.2. Карта медиан (карта )
- •9.4.3. Карты « »
- •9.4.4. Метод средних арифметических значений и
- •9.4.4. Контрольные карты по неизмеримым
- •Карта «р»
- •Карта «с».
2 .3. Вероятность попадания случайной величины
на заданный участок.
При
решении практических задач, связанных
со с.в., часто оказывается необходимым
вычислять вероятность того, что с.в.
примет значение, заключенное в некоторых
пределах, например, от
![]() до
до
![]() .
Это событие мы будем называть попаданием
с.в. на участок от
до
.
Условимся для определенности левый
конец
включать в участок (
,
),
а правый не включать. Тогда попадание
с.в. Х на участок (
,
)
равносильно выполнению неравенства
.
Это событие мы будем называть попаданием
с.в. на участок от
до
.
Условимся для определенности левый
конец
включать в участок (
,
),
а правый не включать. Тогда попадание
с.в. Х на участок (
,
)
равносильно выполнению неравенства
![]() Х
<
.
Х
<
.
Выразим вероятность этого события через функцию распределения
величины Х. Для этого рассмотрим 3 события:
событие А, состоящее в том, что Х< ;
событие B, состоящее в том, что X< ;
событие C, состоящее в том, что X < .
У читывая, что А = В + С, по теореме сложения вероятностей имеем
Р ( Х < ) = P ( X< ) + P ( ); или
F ( ) = F ( ) + P ( X < ); откуда
P ( X < ) = F ( ) – F ( ),
т.е. вероятность попадания случайной величины на заданный участок равна приращению функции распределения на этом участке.
Следствие
из этого вывода: вероятность
любого отдельного значения н.с.в. равна
нулю, т.е. при
![]() Р( Х ) = 0.
Р( Х ) = 0.
2.4. Плотность распределения
Пусть
имеется непрерывная величина Х с функцией
распределения F
(x),
которую мы предположим непрерывной и
дифференцируемой. Вычислим вероятность
попадания этой случайной величины на
участок от х до х +![]() х:
х:
P (x < X < x + x <) = F (x + x) – F (x),
т.е. приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка, т.е. среднюю вероятность, приходящуюся на единицу длины на этом участке и будем приближать x к нулю. В пределе получим производную от функции распределения:
lim F (x + x) – F (x)/ x = F/ (x) = f (x)
x
0
![]()
Функция f (x) - производная функции распределения - характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе "плотностью вероятности") непрерывной случайной величины X. Иногда функцию f (x) называют также дифференциальной функцией распределения или дифференциальным законом распределения величины X. Кривая, изображающая плотность распределения случайной величины, называется кривой распределения. Плотность распределения, также как и функция распределения, есть одна из форм закона распределения. В противоположность функции распределения эта форма не является универсальной, она существует только для н.с.в.
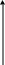 f(x)
f(x)
 Х
Х
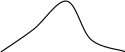
Рассмотрим непрерывную случайную величину с плотностью распределения и элементарный участок dx, примыкающий к точке x. Вероятность попадания случайной величины X на этот участок равна f(x)d(x). Величина f(x)dx называется элементом вероятности. Геометрически это есть площадь элементарного прямоугольника, опирающегося на отрезок dx ( Рис. 1).
f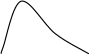 (x)
f
(x)
(x)
f
(x)


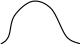






 f(x)
f(x)
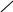 X
X
X
X






![]()
![]()
![]()
Рис.1 Рис.2
Выразим вероятность попадания величины Х на отрезок от до ( Рис. 2) через плотность распределения. Очевидно, она равна сумме элементов вероятности на всем этом участке, т.е. интегралу:
Р(
< X
<
)
=
![]() f(x)dx
f(x)dx
Геометрически вероятность попадания величины X на участок ( , ) равна площади кривой распределения, опирающейся на этот участок. Если выразить функцию распределения через плотность, то:
F
(x)
= P
(-
<
X
< x
) =
![]() f(x)dx.
f(x)dx.
Геометрически F(x) есть площадь кривой распределения, лежащая левее точки x.
 f(x)
f(x)







 х
Х
х
Х
Укажем основные свойства плотности распределения:
1.
Плотность распределения есть
неотрицательная функция: f(x)![]() 0. Это свойство вытекает непосредственно
из того, что функция распределения есть
неубывающая функция.
0. Это свойство вытекает непосредственно
из того, что функция распределения есть
неубывающая функция.
2.
Интеграл в бесконечных пределах от
плотности распределения равен единице:
![]() f(x)dx
=1, так как F(
)
= 1.
f(x)dx
=1, так как F(
)
= 1.
Геометрически это означает, что площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
Пример. Случайная величина Х распределена по закону "прямоугольного треугольника" в интервале (0,а). Необходимо:
а) написать выражение плотности распределения;
б) найти функцию распределения F(x);
в) найти вероятность попадания случайной величины X на участке от a/2 до a.
Решение. Используем свойства линейной функции у = кх + в: к = -2/аа (площадь треугольника S = а/2, у = 2/а) ; к= -2/а2 ;
f(x) = 2/a (1-x/a)
 f(x)
f(x)


 0
при
x < 0;
0
при
x < 0;
f
 (x)
= 2/a
(1-x/a)
при
0
x
a;
(x)
= 2/a
(1-x/a)
при
0
x
a;
0 при x > 0.
X
 a
a
 F(x)
=
2/a
(1-x/a)dx
= 2/a
x-
x2/a2
= x/a
(2-x/a)
F(x)
=
2/a
(1-x/a)dx
= 2/a
x-
x2/a2
= x/a
(2-x/a)
![]() ;
;
0 при х < 0 ;
F(x) = x/a (2-x/a) при 0 < x < a ;
1 при х > a ;
F(a) – F( a/2) =1 – 3/4 = 1/4.
