8.3.4. Полный факторный эксперимент

и математическая модель.

Вернемся к матрице 2². Для движения к точке оптимума нужна линейная модель y = b₀ + b₁x₁ + b₂x₂ . Наша цель - найти по результатам эксперимента значения неизвестных коэффициентов модели. До сих пор, говоря о линейной модели сил, не останавливались на важном вопросе о статистической оценке ее коэффициентов. Теперь необходимо сделать ряд замечаний по этому поводу. Можно утверждать, что эксперимент проводится для проверки гипотезы о том, что линейная модель = ₀+ ₁x₁+ ₂x₂ адекватна. Греческие буквы использованы для обозначения "истинных" генеральных значений соответствующих неизвестных. Эксперимент, содержащий конечное число опытов, позволяет получить только выборочные оценки для коэффициентов уравнения y = b₀ + b₁x₁ + b₂x₂ .

Не говоря пока о точности и надежности оценок, займемся вычислением оценок коэффициентов. Их можно рассчитать по формуле: b_j = x_ij y_i / N (8.3) , j = 0, 1, ... , k .

Обоснование формулы будет дано позднее.

Воспользуемся этой формулой для подсчета коэффициентов b₁ и b₂ для матрицы 2²: b₁ = [(-1)y₁ + (+1)y₂ + (-1)y₃ + (-1)y₄] / 4 ;

b₂ = [(-1)y₁ + (-1)y₂ + (+1)y₃ + (+1)y₄] / 4 ;

Благодаря кодированию факторов расчет коэффициентов превратился в простую арифметическую процедуру. Для подсчета коэффициента b₁ используется вектор-столбец X₁, а для b₂ – X₂. Остается определить b₀. Если уравнение y = b₀ + b₁x₁ + b₂x₂ справедливо, то оно верно и для средних арифметических значений переменных: ₀ = b₀ + b_{1 1} + b_{2 2}. Но в силу свойства симметрии ₁ = ₂ =0 ₀ = b₀ , т.е. b₀ есть среднее арифметическое значение параметра оптимизации. Чтобы его получить, необходимо сложить все y_i и разделить их на число опытов. Чтобы привести эту процедуру в соответствие с формулой для вычисления коэффициентов, в матрицу планирования удобно ввести вектор-столбец фиктивной переменной X₀, которая принимает во всех опытах значение (+1). Это было уже учтено в записи формулы (8.3), где j принимало значение от 0 до k..Теперь можно найти все коэффициенты линейной модели y = b₀ + b₁x₁ + b₂x₂ .

Пример 8.1. Исследуется влияние различных факторов на разностенность изделия при вытяжке с утонением в среднем сечении (рис.6).

а а

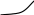
Рис.6 Эскиз исследуемой детали

В качестве независимых переменных выбраны следующие факторы; X₁ -угол вытяжной матрицы; Х₂- угол между осью пуансона и направлением хода ползуна; Х₃ - разностенность заготовки в среднем сечении. По условиям проведения эксперимента составлена таблица. (8.4)

Таблица 8.4

Обо-значение фак- тора	Наименование фактора	Размерность	Область эксперимента
			Низший уровень “-“	Основной уровень “0”	Верхний уровень “+”	Интервал варьирования
Х Х Х	Угол вы- тяжной матрицы Угол между осью пуансона и направле- нием хода ползуна Разностен- ность за- готовки в среднем сечении	Град. Рад . Мkm	5 0,00155 36	11,8 0,00238 58	18 0,00310 82	6,5 0,00073 23

В табл. 8.5. представлены матрица планирования полного факторного эксперимента и результаты опытов. Поскольку каждый эксперимент может нести в себе какую то ошибку, для ее уменьшения каждый опыт повторялся трижды в одних и тех же условиях. Значения параметра оптимизации, указание в колонке Y, есть среднее арифметическое параллельных опытов. Например,

Таблица 8.5

№ точки плана	Хо	X1	Х2	Х3		Y1	Y2	Y3
1 2 3 4 5 6 7 8	+ + + + + + + +	- + - + - + - +	- - + + - - + +	- - - - + + + +	24 20 22 25 55 50 55 55	22 20 16 21 53 48 52 53	24 16 24 25 55 49 57 54	26 24 26 29 57 53 56 58

Предполагаем моделировать результаты эксперимента полиномом

первой степени:

Подставив результаты эксперимента в формулу (8.6), вычис-

лим последовательно коэффициенты b₀, b₁, b₂ , b₃ :

b₀= 38.25; b₁= -0.75; b₂=1; b₃= 15.5.

Полученные значения подставляем в уравнение полинома первой

степени:

y=38.25-0.75x₁+x₂+15.5x₃.

Коэффициенты при независимых переменных указывают на силу влияния факторов. Чем больше численная величина коэффициента, тем большее влияние оказывает фактор. Если коэффициент имеет знак " +", то с увеличением значения фактора параметр оптимизации увеличивается, а если "-", то уменьшается. Величина коэффициента соответствует вкладу данного фактора в величину параметра оптимизации при переходе фактора с нулевого уровня на верхний или нижний уровень.

Иногда удобно оценивать вклад фактора при переходе от нижнего уровня к верхнему уровню. Вклад, определенный таким образом, называется эффектом фактора (еще его называют основным или главным эффектом). Он численно равен удвоенному коэффициенту b_j. Для качественных факторов, варьируемых на двух уровнях, основной уровень не имеет физического смысла. Поэтому понятие "эффект фактора" является здесь естественным.

Планируя эксперимент, на первом этапе мы стремимся получить линейную модель. Однако у нас нет гарантии, что в выбранных интервалах варьирования процесс описывается линейной моделью. Существуют способы проверки пригодности линейной модели, которые мы рассмотрим позднее. А если модель нелинейна, как количественно оценить нелинейность, пользуясь полным факторным экспериментом?

Один из часто встречающихся видов нелинейности связан с тем, что эффект одного фактора зависит от уровня, на котором находится другой фактор. В этом случае говорят, что имеет место эффект взаимодействия двух факторов. Полный факторный эксперимент позволяет количественно оценивать эффекты взаимодействия. Для этого надо, пользуясь правилом перемножения столбцов, получить столбец произведения двух факторов. При вычислении коэффициента, соответствующего эффекту взаимодействия, с новым вектор-столбцом можно обращаться также, как с вектор-столбцом любого фактора. Для полного факторного эксперимента 2² матрица планирования с учетом эффекта взаимодействия представлена в таблице.

Рассмотренные ранее свойства матрицы сохраняются.

№	X0	X1	X2	X1X2	Y
1 2 3 4	+ + + +	+ - - +	+ + - -	+ - + -	y1 y2 y3 y4

Теперь модель выглядит следующим образом:

y = b₀ + b₁x₁ + b₂x₂ +b₁₂x₁x₂

Коэффициент b₁₂ вычисляется обычным путем:

b₁₂ = [(+1)y₁+ (-1)y₂ + (+1)y₃ + (-1)y₄] / 4.

Столбцы X₁ и X₂ задают планирование - по ним непосредственно определяются условия опытов, а столбцы X₀ и X₁₂ служат только для расчета.

С ростом числа факторов, число возможных взаимодействий быстро растет. Мы рассмотрели самый простой случай, когда имелось одно взаимодействие. Обратимся теперь к полному факторному эксперименту 2

Таблица 8.6

№ опыта	X0	X1	X2	X3	X2X2	X1X3	X2X3	X1X2X3	Y
1 2 3 4 5 6 7 8	+ + + + + + + +	- + - + - + - +	- - + + - - + +	- - - - + + + +	+ - - + + - - +	+ - + - - + - +	+ + - - - - + +	- + + - + - - +	y1 y2 y3 y4 y5 y6 y7 y8

Столбец эффекта взаимодействия Х₁Х₂Х₃ получается перемножением всех трех столбцов и называется эффектом взаимодействия второго порядка. Эффект взаимодействия двух факторов называется эффектом взаимодействия первого порядка. Вообще эффект взаимодействия максимального порядка в полном факторном эксперименте имеет порядок, на единицу меньший числа факторов.

Полное число всех возможных эффектов, включая линейные эффекты и взаимодействия всех порядков, равно числу опытов полного факторного эксперимента. Чтобы найти число возможных взаимодействий некоторого порядка, можно воспользоваться обычной формулой числа сочетаний:

C = k! / m! (k – m)!

где k - число факторов, m - число элементов во взаимодействии.

Так, для плана 2³ число взаимодействий первого порядка

.

Пример 8.2. По данным примера 8.1. определить коэффициенты уравнения .регрессии с учетом эффектов взаимодействия.

y=b₀+b₁x₁+b₂x₂+b₃x₃+b₁₂x₁x₂+b₁₃x₁x₃+b₂₃x₂x₃+b₁₂₃x₁x₂x₃..

Коэффициенты b₀, b₁, b₂, b₃ найдены ранее (пример 8.1). Для вычисления остальных коэффициентов воспользуемся формулой 8.3, таблицей 8.6 и значениями параметра оптимизации по таблице 8.5.

b₁₂ = (+24-20-22+25+55-50-55+55)/8= 1,5;

b₁₃ = (+24-20+22-25-55+50-55+55)/8=-0,5;

b₂₃ = (+24+20-22-25-55-50+55+55)/8=0,25;

b₁₂₃= (-24+20+22-25+55-50-55+55)/8=-0,25;

Уравнение регрессии с учетом эффектов взаимодействия будет иметь следующий вид:

y=38.25-0.75x₁+x₂+15.5x₃+1.5x₁x₂-0.5x₁x₃+0.25x₂x₃-0.25x₁x₂x₃.

После вывода уравнения регрессии необходимо провести статистический анализ результатов моделирования.