Координаты характерных точек кривой

нормального распределения

характерные точки	абсцисса	ордината
вершина кривой		f = 0,4 nC/S
точка перегиба	S	fs = 0,242 nC/S
точка перегиба	2S	f2s = 0,054nC/S
точка перегиба	3S	f3s = 0

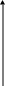f

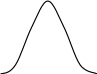0,4 nC/S

0,242 nC/S

0,054nC/S

x

s s

2s 2s

3s 3s

Замечание. Сопоставление эмпирического распределения с законом нормального распределения можно производить также при помощи функции Лапласа (t) . Для этой цели необходимо сначала для каждого интервала значений x вычислить t по формуле: t = (x_в- )/S, где x_в - верхнее значение интервала. Затем по найденному t по таблицам определяется (t) , а по (t) для каждого интервала определяют интегральную функцию F(x) = 0,5 + (t). По величине F(x) можно определить теоретическую частоту f^/. Для первого интервала f = F₁(x)n; для второго - f = [F₂(x) – F₁(x)]n; для i – го – f_i = [F_i(x) – F_i-

₁(x)]n.

5.3. Сопоставление эмпирического распределения

с распределением по закону равной вероятности.

Для вычисления теоретических частот f^/ можно воспользоваться следующим приближенным равенством: f(x) = 1/(b – a) f^//nC, откуда f^/ = nC/(b – a) , где n - объем совокупности,

C - цена интервала, b и а- предельные значения случайной величины X. Учитывая, что M(x) = (a + b)/2 , (x) = (b – a)/2 и заменяя параметры их оценками и S, можно определить a и в, решив совместно два уравнения:

а = - S ; b = + S .

Пример. По данным таблицы вычислены и S : = 0,094; S =0,092; C=0,044.

Xi	0,03	0,05	0,07	0,09	0,11	0,13	0,15	0,17
fi	13	15	16	12	14	11	10	9

Учитывая, что в – а =2S , рассчитаем последовательно:

f^/ = 100 0,02 / 2 0,044 1,73 = 13,2 ;

a = 0,094 – 0,044 1,73 = 0,018;

b = 0,094 + 0,044 1,7 = 0,17

5.4. Статистическая проверка гипотез.

Статистическая проверка гипотез, т.е. предположений, относящихся к эмпирическим распределениям изучаемых случайных величин, играет важную роль в статистических исследованиях.

Если эмпирическая кривая распределения большой выборки по своему внешнему виду приближается к какому-либо теоретическому закону распределения, то возникает вопрос, можно ли данную выборку рассматривать как выборку из генеральной совокупности, имеющей распределение именно по этому закону. Решение этого вопроса имеет важное значение для исследователя, так как знание закона распределения изучаемой величины позволяет извлечь из экспериментов дополнительную информацию.

Если производится две серии испытаний с фактором А и без него, и в результате получаются разные значения средних и дисперсии изучаемой переменной величины, то возникнет вопрос, является ли это различие в средних и дисперсиях влиянием фактора А или оно носит чисто случайный характер.

Решение перечисленных и им подобных задач в математической статистике производится путем постановки и проверки так называемой "нулевой гипотезы". При этом под "нулевой гипотезой" подразумевается допущение об отсутствии интересующего нас различия между выборками или их статистическими характеристиками. Например, нас интересует, можно ли по полученному распределению в большой выборке из генеральной совокупности считать, что последняя имеет нормальное распределение. Для того чтобы прийти к вполне определенному заключению, хотя бы и вероятностного характера, мы делаем гипотетическое допущение, что распределение выборки несущественно отличается от нормального и, следовательно, на основании закона больших чисел можно считать, что и генеральная совокупность имеет нормальное распределение. Другими словами, мы выдвигаем "нулевую гипотезу" об отсутствии различия между эмпирическим распределением и теоретическим нормальным или гипотезу о том, что данная выборка взята из нормальной совокупности. Теперь надо проверить эту гипотезу и в результате проверки либо отбросить ее, либо принять.

Для проверки гипотез в математической статистике пользуются рядом критериев, которые называют в этом случае критериями согласия. Для того, чтобы принять или забраковать гипотезу при помощи этих критериев, установлены уровни значимости их. Уровень значимости представляет собой достаточно малое значение вероятности, отвечающее событиям, которые в данной обстановке исследования можно считать практически невозможным. Обычно принимают пяти-двух или однопроцентный уровень значимости. В технике чаще всего принимают пятипроцентный уровень значимости ( = 0,05; 0,02; 0,01). С уменьшением уровня значимости расширяется область допустимых значений критерия и вместе с тем теряется его чувствительность, так как повышается вероятность принять гипотезу даже в тех случаях, когда эта гипотеза неверна. Но вместе с тем выбор достаточно малого уровня значимости гарантирует от возможности неправильно забраковать верную гипотезу. Статистические приемы проверки гипотез не обладают полной определенностью. Если используемый критерий попадает в область допустимых значений, то нельзя еще сделать вывода о правильности гипотезы, а можно лишь заключить, что наблюдаемое значение критерия не противоречит этой гипотезе, что можно признать допустимость гипотезы до тех пор, пока более обстоятельные исследования с помощью более точных критериев или при увеличенном числе наблюдений не подтвердят это или не приведут к противоположному заключению. Поэтому статистическими методами нельзя пользоваться формально, а необходимо их сочетать с анализом физической сущности изучаемого явления. Когда гипотеза, основанная на теоретическом анализе физической сущности явления, подтверждается также статистическими приемами, то достоверность ее можно считать достаточно надежной.