2.4 Геометрическое моделирование

В геометрических математических моделях, помимо сведений о взаимном расположении элементов объекта исследования, даются сведения об его форме.

Для отображения геометрических свойств объектов со сравнительно несложными поверхностями математические модели получают в аналитической или алгебрологической форме. Например, аналитическое уравнение плоскости имеет вид , где , , – пространственные координаты, , , , – коэффициенты уравнения. Алгебрологические геометрические модели описывают объект логической функцией условий, выражающих принадлежность точек тем или иным областям. Например, пусть области , , , определены на плоскости с помощью неравенств следующим образом:

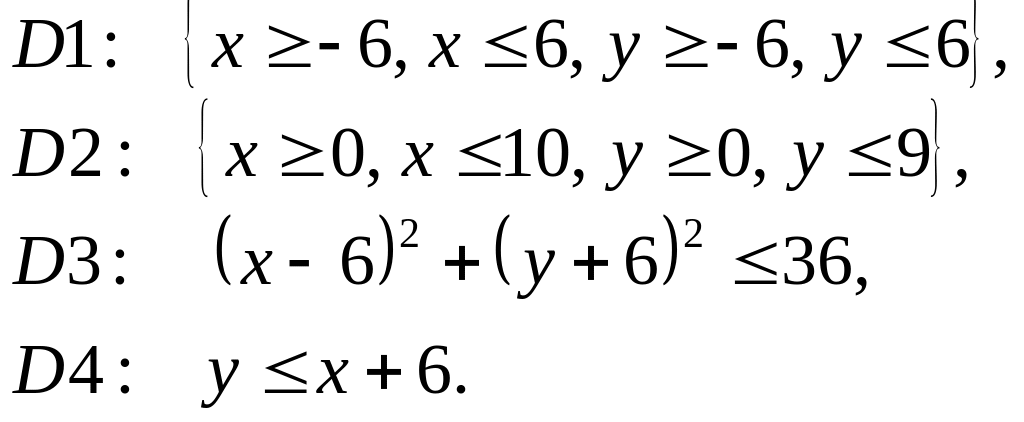
Тогда алгебрологическая модель геометрического объекта , записанная с помощью соотношения:

на графике может быть изображена заштрихованной частью плоскости (рисунок 17).

Рисунок 17  Геометрическое представление алгебрологической модели

Для отображения геометрических свойств деталей со сложными поверхностями математические модели получают каркасным или кинематическим способом. Каркасные математические модели представляют собой конечные множества геометрических элементов, например, точек или кривых, принадлежащих моделируемой поверхности.

В кинематических математических моделях поверхность или твердое тело задаются в параметрическом виде. Такую поверхность (тело) можно представить как результат перемещения в трехмерном пространстве некоторого объекта, в частности, кривой, называемой образующей, по направляющей линии. На рисунке 18 показан пример трехмерной геометрической модели, полученной «вращением» контура сечения области вокруг оси на 270⁰.

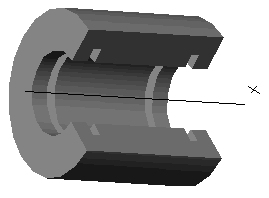
Рисунок 18 – Пример геометрической модели, полученной кинематическим способом

Если в геометрическом описании объекта удается выделить параметры, однозначно его определяющие и в то же время имеющие простую связь с его формой, геометрические модели считаются каноническими. Примером канонической модели является плоский многоугольник с известными координатами вершин. В том случае, когда инженер или исследователь имеет дело с типовыми геометрическими фрагментами, целесообразно описание и создание макромоделей. При автоматизированном оформлении конструкторской документации обычно формируют электронные библиотеки макромоделей, а затем используют их для описания стандартных графических изображений, например, зубчатых колес, крепежных соединений, подшипниковых узлов и т.п.

Фрактальные геометрические модели используются для отражения свойств нерегулярных, но самоподобных геометрических структур. Кроме самоподобия, проявляющегося во фракталах при любых приближениях, для них также характерна так называемая дробная размерность [1]. Широкое распространение фрактальных структур в природе объясняется тем, что геометрическое подобие есть основной закон роста природных объектов. Закон изменения формы фрактала, как правило, реализуется алгоритмически.

2.5 Функциональное моделирование

Исходной информацией при построении математических моделей процессов функционирования систем служат данные о назначении и условиях работы исследуемой (проектируемой) системы. Эта информация определяет основную цель моделирования системы и позволяет сформулировать требования к разрабатываемой математической модели.

Построение функциональных моделей в первую очередь характеризуется выбором множества так называемых фазовых переменных. В машиностроительных приложениях примерами фазовых переменных являются: сила, скорость, деформация, напряжение, температура, тепловой поток и т.п. Классический метод построения функциональных математических моделей физических процессов состоит в применении фундаментальных законов природы (сохранение энергии, материи, импульса) к конкретной ситуации. Эти законы общепризнаны и их обоснованность не вызывает сомнений. Другой метод получения функциональных моделей, по универсальности сопоставимый с только что указанным, – применение вариационных принципов. В его основе лежит достаточно общее утверждение, что из всех возможных вариантов поведения исследуемого объекта выбираются лишь те, которые удовлетворяются определенному условию. Обычно согласно этому условию некоторая связанная с объектом математическая величина (функционал) стремится к экстремальному значению. Типичным примером в данном случае является вывод основных соотношений метода конечных элементов – распространенного в вычислительной механике средства инженерного анализа объектов [3, 12, 13].

Вместе с тем часто при попытке построить математическую модель какого-либо сложного явления либо невозможно прямо указать фундаментальные законы или вариационные принципы, которым оно подчиняется, либо вообще нет уверенности в существовании нужных формулировок. В этом случае продуктивным может быть метод использования аналогий, в основе которого лежит известный в технических и естественных науках факт, что закономерности протекания многих различных по своей природе явлений в математической форме описываются аналогичными по структуре уравнениями. Другие средства построения функциональных математических моделей предоставляют хорошо разработанные методы статистической обработки экспериментальных данных и методы математического программирования.

Успешные попытки функционального моделирования информационных процессов в технологических системах и технических объектах традиционно связаны с достижениями математической теории вероятности, теоретической информатики, теорией массового обслуживания и теорией автоматического управления. Области применения математических моделей информационных процессов: программное управление оборудованием, управление процессами, технологическими системами, производственными участками, цехами, проектирование средств измерения [13].

Кроме того, при функциональном моделировании широко используют экспериментальные факторные модели, которые называют также регрессионными моделями.

Регрессионную модель можно представить выражением:

^,

где – вектор управляемых параметров (факторов) объекта;

– вектор неуправляемых параметров (факторов) объекта;

– вектор коэффициентов модели;

– вектор зависимых (выходных) параметров объекта, называемых также откликом.

Вид функции отклика выбирается исследователем на основе анализа информации об объекте, часто набора функций определенного типа, например:

, , .

Коэффициенты подлежат определению на основе обработки результатов натурного или вычислительного эксперимента, например, с помощью интерполяции или аппроксимации по методу наименьших квадратов.

Если в эксперименте существуют только неуправляемые факторы , то его называют пассивным, если только управляемые факторы – активным.

Две важные особенности экспериментальных факторных моделей:

1) они являются статистическими, описывая объект в среднем;

2) они являются адекватными лишь в области факторного пространства , в которой реализован эксперимент.

Методы построения экспериментальных факторных моделей рассматриваются в теории планирования эксперимента.

В случае если функция отклика задает соответствие между величинами, характеризующими ход конкретного процесса или явления на производстве, ее часто называют производственной.

Примеры экспериментальных факторных моделей: эмпирические формулы для скорости и силы резания.