Частотные критерии

Особенности частотных критериев

1. Наглядность в определении устойчивости, т.к. судят по расположению кривой в комплекс­ной плоскости.

2. Возможность суждения об устойчивости, когда нет математического описания системы (по экспериментальным данным).

3. Возможность суждения о некоторых других показателях качества.

Критерий устойчивости Михайлова

Частотный характеристический вектор имеет вид

где

Свойства характеристического вектора

1) При =0

2) Модуль характеристического вектора вдоль одной из полу­осей комплексной плоскости, что определяется степенью характеристического уравнения.

n=1 (а)

n=2 . (б)

Если n=3, то (в)

Т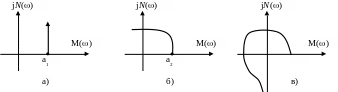 очная формулировка критерия Михайлова.

Для того, чтобы САР была устойчива, необходимо и достаточно, чтобы кривая Михайлова, начинаясь на вещественной положительной оси при =0 при изменении  от 0 до  последовательно обходила n квадрантов, нигде не превращаясь в ноль, обращение А(j) в ноль означает наличие мнимых корней.

Е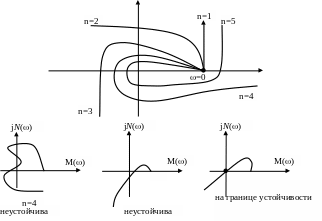 сли есть мнимые корни  система на границе устойчивости.

Из (*) определяем К_кр.

Из второго уравнения для линейной системы К_кр:

N() = 0  _кр  М() = 0  К_кр

Кривую Михайлова можно построить 2-мя способами:

1. по годографам отдельных звеньев (трудоемка)

2. разложением кривой Михайлова на вещественную и мнимую часть и получением ряда из значений при разных частотах.

Следствие кривой Михайлова.

А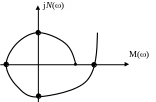 нализ кривой Михайлова показывает, что вещественная часть обращается в ноль тогда, когда годограф проходит через мнимую ось, а мнимая обращается в ноль, когда годограф проходит через вещественную ось, что говорит о том, что корни уравнений М()=0 и N()=0 чередуются.

Из этого вывод: САР будет устойчива, если корни уравнений и чередуются, а общее число корней равно степени характеристического уравнения.

Правило определения устойчивости:

Определяются корни уравнений и и располагаются в порядке возрастания. Если порядок соответствует чередованию, то система устойчива.

₀ < ₁ < ₂ < ₃ < ₄ < …

Критерий устойчивости Найквиста

Он позволяет судить об устойчивости замкнутой системы САР по АФХ разомкнутой системы.

Рассмотрим следующие случаи критерия Найквиста

1) Система в разомкнутом состоянии устойчива l=0.

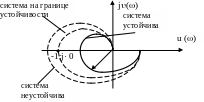Можно показать, что условие (1) может быть выполнено в следующем случае, а именно: замкнутая САР будет устойчива, если при изменении  от 0 до  АФХ разомкнутой системы не охватывает точки с координатами С истема на грани устойчивости:

то:

2) Система в разомкнутом состоянии неустойчива .

Число правых корней не равно нулю. Вектор F(j) должен охватывать начало координат ^l/₂ раз в положительном направлении.

Если разомкнутая САУ неустойчива, то для устойчивости замкнутой САУ необходимо, чтобы АФХ разомкнутой системы при изменении =0 ÷ ∞ охватывала точку с координатами (1;j0) ^l/₂ раз в положительном направлении (против часовой стрелки).

П ример.

При Т₁< Т₂ система неустойчива.

Упрощенная формулировка критерия Найквиста применительно к логарифмическим характеристикам если разомкнутая система устойчива.

Ф ормулировка. Если разомкнутая САР устойчива, то замкнутая САР будет устойчива, если ЛАХ разомкнутой системы пересечет ось lg раньше, чем ЛФХ достигнет линии -