Лекция №3. Оценка параметров случайных величин.

1. Оценка как функция случайных величин – результатов наблюдений.

Рассмотрим вопрос об определении числовых характеристик случайной величины Х по результатм n независимых опытов. Обозначим наблюденные значения случайной величины

Х₁, Х₂, …, Х_n.

Их можно рассматривать как n «экземпляров» случайных величин Х, то есть n независимых случайных величин. Каждая из которых распределена по тому же закону, что и случайная величина Х.

Обозначим ã оценку параметра а. Любая оценка, вычисленная на основе материала Х₁, Х₂, …, Х_n должна представлять собой функцию этих величин:

ã=φ(Х₁, Х₂, …, Х_n)

и, следовательно, сама является величиной случайной. Такая оценка называется «точечной». Закон распределения ã зависит, во-первых, от закона распределения величины Х (и, в частности, от самого неизвестного параметра а): во-вторых, от числа опытов n. В принципе этот закон распределения может быть найден известными методами теории вероятностей.

2. Критерии оценок.

• Состоятельность.

Если при увеличении числа опытов n оценка ã сходится по вероятности к параметру а, то такая оценка называется состоятельной.

• Несмещенность.

Если математическое ожидание оценки ã равно оцениваемому параметру а, т. е. выполняется

М[ã]=a,

то такая оценка называется несмещенной.

• Эффективность.

Если оценка ã обладает по сравнению с другими оценками наименьшей дисперсией, т. е.

D[ã]=min,

то она назывется эффективной.

На практике не всегда удается удовлетворять всем этим требованиям. Например, может оказаться, что, даже если эффективная оценка существует, формулы для ее вычисления оказываются слишком сложными, и приходится удовлетворяться другой оценкой, дисперсия которой несколько больше. Иногда применяются – незначительно смещенные оценки. Однако выбору оценки всегда должно предшествовать ее критическое рассмотрение со всех перечисленных выше точе зрения.

3. Оценки для математического ожидания и дисперсии.

Пусть имеется случайная величина Х с математическим ожиданием m и дисперсией D; оба парамеира неизвестны. Над величиной Х произведено n независимых опытов, давших результаты X₁, X₂, . . . , X_n.

В качестве оценки для математического ожидания естественно взять статистическое среднее m*:

Можно доказать, что эта оценка является состоятельной и несмещенной. Если величина Х распределена по нормальному закону, дисперсия будет минимально возможной, т. е. оценка является эффективной. Для других законов распределения это может быть и не так.

Если в качестве оценки дисперсии взять статистическую дисперсию D*

,

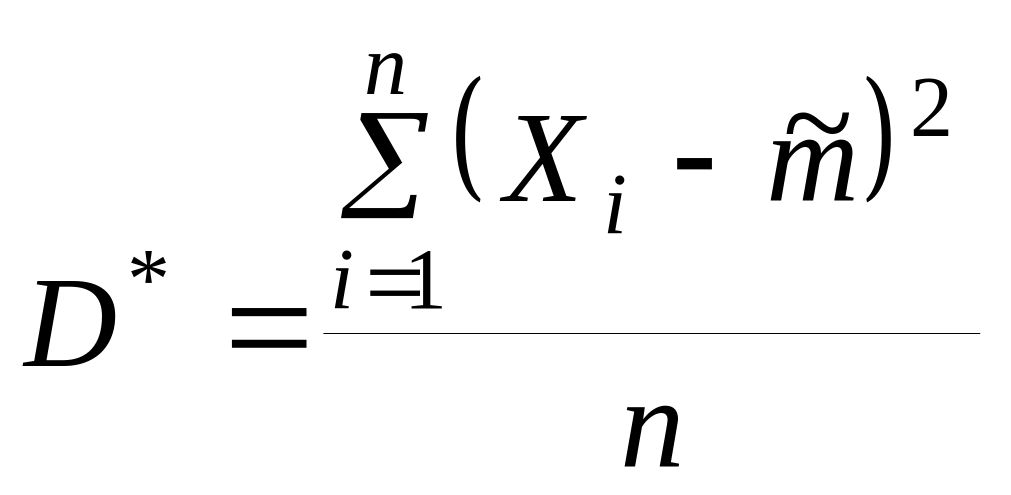то при проверки окажетя, что эта оценка состоятельная, но не является несмещенной. Ее математическое ожидание:

Пользуясь оценкой D* вместо дисперсии D, мы будем совершать некоторую систематическую ошибку в меньшую сторону. Чтобы ликвидировать это смещение, достаточно ввести поправку, умножив величину D* на n/(n-1).

Оценка

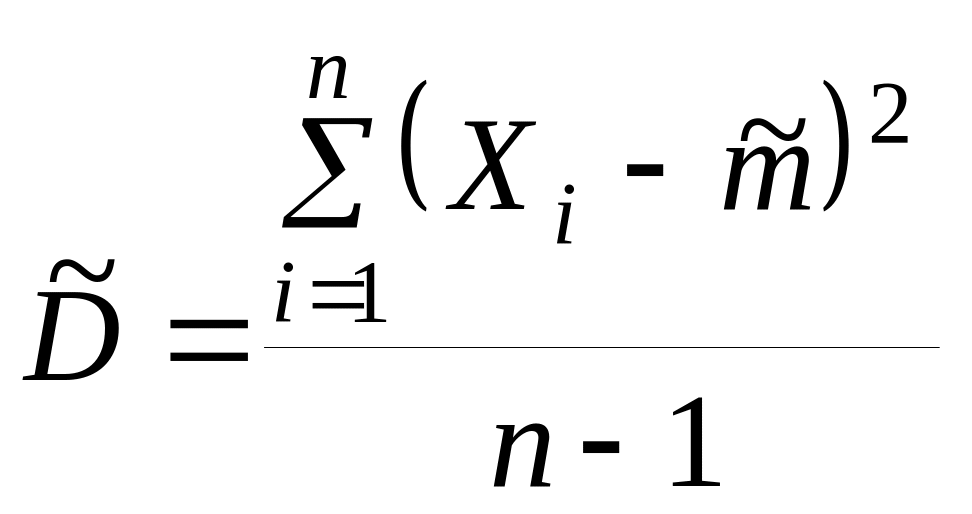
называется «исправленной» статистической дисперсией. Эта оценка состоятельная и несмещенная, но эффективной она не является. Однако в случае нормального распределения она является «асимптотически эффективной», то есить при увеличении n отношение ее дисперсии к минимально возможной неограниченно приближается к единице.

4. Метод моментов для точечной оценки параметров распределения.

Это метод основан на том, что начальные и центральные статистические моменты являются состоятельными оценками соответственно начальных и центральных теоретических моментов того же порядка. Метод предложен К. Пирсоном и состоит в приравнивании теоретических моментов рассматриваемого распределения соответствующим стаистическим моментам того же порядка.

Пусть задан вид плотности распределения f(x,θ), определяемый одним неизвестным параметром θ. Требуется найти точечную оценку параметра θ.

Следуя методу моментов, приравняем начальный теоретический момент первого порядка начальному статистическому моменту первого порядка:

m=m*

Математическое ожидание, как видно из соотношения

есть функция от θ, поэтому выражение

можно рассматривать как уравнение с одним неизвестным θ. Решив это уравнение относительно параметра θ, тем самым найдем его точечную оценку.

Пусть задан вид плотности распределения f(x;θ₁,θ₂), определяемый неизвестными параметрами θ₁ и θ₂. Для отыскания двух параметров необходимы два уравнения относительно этих параметров. Следуя методу моментов приравняем начальный теоретический момент первого порядка начальному статистическому моменту первого порядка и центральный теоретический момент вторго порядка центральному статистическому моменту второго порядка:

m=m* D=D*

Учитывая, что

и

можем составить систему двух уравнений с двумя неизвестными

Решив эту систему относительно неизвестных парамеиров θ₁ и θ₂ ,тем самым получим их точечные оценки.

5. Метод наибольшего правдоподобия.

Предложен Р. Фишером.

Дискретные случайные величины. Пусть Х – дискретная случайная величина, которая в результате n испытаний приняла значения x₁, x₂, . . . , x_n. Допустим, что вид закона распределения величины Х задан, но неизвестен параметр θ, которым определяется этот закон. Требуется найти его точечную оценку.

Обозначим вероятность того, что в результате испытания величина Х примет значение x_i (i=1, 2, . . ., n), через p(x_i; θ).

Функцией правдоподобия дискретной случайной величины Х называют функцию аргумента θ:

,

где x₁, x₂, . . . , x_n – фиксированные числа.

В качестве точечной оценки параметра θ принимают такое его значение θ*, при котором функция правдоподобия достигает максимума. Оценку θ* называют оценкой наибольшего правдоподобия.

Функции L и ln L достигают максимума при одном и том же значении, поэтому вместо отыскания максимума функции L ищут (что удобнее) максимум функции ln L. Функцию ln L назывют логарифмической функцией правдоподобия.

Непрерывные случайные величины. Пусть Х – непрерывная случайная величина, которая в результате n ипытаний приняла значения x₁, x₂, . . . , x_n . Допустим, что вид плотности распределения f(x; θ) задан, но не известен параметр θ, которым определяется эта функция.

Функцией правдоподобия непрерывной случайной величины Х назывют функцию аргумента θ

где x₁, x₂, . . . , x_n – фиксированные числа.

Оценку наибольшего правдоподобия неизвестного параметра распределения непрерывной случайной величины ищут так же, как в случае дискретной величины.

6. Доверительный интервал. Доверительная вероятность.

Чтобы дать представление о точности и надежности оценки ã, в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями. Эти понятия особенно актуальны при малом числе наблюдений, когда точечная оценка ã в значительной мере случайна и приближенная замена а на ã может привести к серьезным ошибкам.

Пусть для параметра а получена несмещенная оценка ã. Мы хотим оценить возможную при этом ошибку. Назначим некоторую достаточно большую вероятность ( нпример, β=0,9, 0,95 или 0,99 ) такую, что событие с вероятностью β можно считать практически достоверным, и найдем такое значение ε, для которого

Тогда диапазон практически возможных значений ошибки, возникающей при замене а на ã, будет ; большие по абсолютной величине ошибки будут появляться только с малой вероятностью.

Перепишем приведнное выше равенство в виде:

Это означает , что с вероятностью β неизвестное значение патаметра а попадает в интервал

I_β=(ã-ε; ã+ε).

Доверительным называют интервал, который покрывает неизвестный параметр с заданной вероятность (надежностью).

Доверительной вероятностью (надежностью) называется вероятность с которой осуществляется неравенство .

Величина а не случайна, зато случаен интервал. Случайно его положение на оси абсцисс, определяемое его центром ã; случайна вобще и длина интервала 2ε, так как величина ε вычисляеися, как правило, по опытным данным. Поэтому лучше толковать величину β не как вероятность «попадания» точки а в интервал I_β, а как вероятность того, что случайный интервал I_β накроет точку а.

Мы рассматривали доверительный интервал симметричный относительно относительно ã, вообще говоря это не обязательно.

Чтобы оценить точность и надежность оценки,нужно знать ее закон распределения. Если бы нам был известен закон распределения величины ã, задача нахождения доверительного интервала была бы весьма проста: достаточно было бы найти такое значение ε, для которого

.

Затруднение состоит в том, что закон распределения оценки ã зависит от закона распределения величины Х и, следовательно, от его его неизвестных параметров (в частности, и от самого параметра а).

7. Доверительный интервал для математического ожидания нормально распределенной случайной величины с известной дисперсией.

Примем без доказательства, что если случайная величина Х распределена нормально, то взяятое в качестве оценки ее математического ожидания статстическое среднее

,

есть случайная величина распределенная нормально, и параметры этого закона следующие:

,

где m, D и σ соответствующие параметры закона распределения случайной величины Х.

Рассмотрим случайную величину . Закон распределения Δ также будет нормальным, а его параметры:

M[Δ]=0, D[Δ]=0, σ_Δ=σ/√n

Определим вероятность попадания случайной величины Δ на отрезок [-α, α]

Обзначим

Задав доверительную вероятность β, по таблице значений интегральной функции Лаплпса легко определить значение u, учитывая что . Затем определяем α

.

Теперь можем записать

,

или

.

Таким образом это доверительный интервал для математического ожидания случайной величины Х, с нормальным законом распределения, при заданной доверительной вероятности β.