3. Вероятность попадания случайной величины на заданный участок

На практике при исследовании случайных величин довольно часто возникает задача определения вероятности попадания значений некоторой случайной величины Х на заданный участок [a,b), т.е. вероятности Р{a Х < b}. Такая вероятность легко определяется с помощью интегральной функции.

В ведем обозначения:

А – событие, которое заключается в том, что Х < а ;

В – событие, которое заключается в том, что Х < b ;

С – событие, которое заключается в том, что a Х < b .

Сложное случайное событие В представляет собой сумму событий А и С (см. рис.4.2): В = А + С.

Поскольку события А и С являются несовместными, то

Р(В) = Р(А) + Р(С).

Откуда

Р(С) = Р(В) – Р(А) = Р{Х < b} – Р{Х < а}.

По определению интегральной функции Р{Х<b} = F(b), Р{Х<а} = F(а). Следовательно,

Р(С) = F(b) – F(a).

Таким образом, вероятность попадания случайной величины на заданный участок определяется по формуле

. (4.2)

Пример 4.2. В условиях прим.4.1 определить вероятность попадания случайной величины Х на участок [2,5; 3,5), т.е. вероятность Р{2,5 X < 3,5}.

Р ешение. В данном случае левая граница участка a = 2,5 , а правая b = 3,5. Подставляя в формулу (4.2) значения аргумента интегральной функции и вычисляя значения интегральной функции на границах заданного участка, получаем искомый результат:

Р{2,5 X < 3,5} = F(b) – F(a) =

=F(3,5) – F(2,5) = 1 – 0,271 = 0,729 .

Искомая вероятность и значения интегральной функции F(х) в условиях примера легко определяются по графику интегральной функции (см. рис.4.3).

Лекция № 6 Числовые характеристики случайных величин.

Полную информацию о случайной величине дает ее распределение вероятности. Однако, часто такими данными исследователи не располагают, да и оно не является обязательным. Достаточно охарактеризовать случайную величину несколькими числами. Числовые характеристики случайных величин количественно определяют их свойства, позволяют проводить сравнительный анализ случайных величин, давать оценку ожидаемым результатам опыта и многое другое.

1. Характеристики положения случайной величины на числовой оси.

К числовым характеристикам положения случайной величины на числовой оси относятся:

1. математическое ожидание;

2. мода;

3. медиана.

1. 1. Математическое ожидание

Определение 6.1.

Математическим ожиданием называется средневзвешенное по вероятностям значение случайной величины.

Математическое ожидание характеризует смещение значений случайной величины на числовой оси х относительно начала координат. Математическое ожидание иногда называют просто средним значением с. в.

Математическое ожидание случайной величины будем обозначать как m_x или M(X).

Математическое ожидание не случайное число, которое в зависимости от типа случайной величины определяется по формуле:

(6.1)

Размерность математического ожидания совпадает с размерностью с. в. Х.

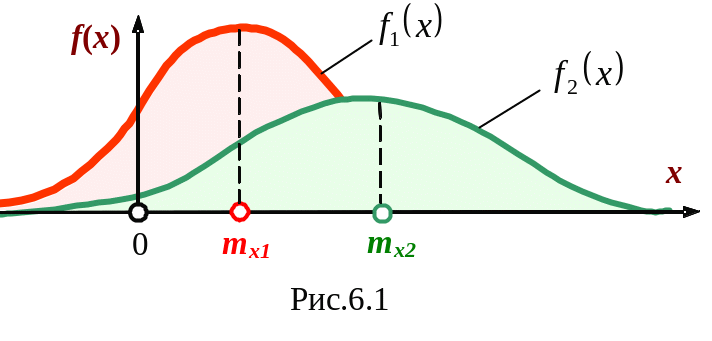
На рис.6.1. показаны две непрерывные случайные величины, заданные в виде плотности распределения и отличающиеся друг от друга математическими ожиданиями (m_х2 > m_х1).

1. 2. Мода

Определение 6.2.

Модой называют наиболее вероятное значение случайной величины (т.е. то для которого вероятность p_i, или плотность распределения f(x) достигает максимального значения).

Обозначается мода случайной величины символом  .

Таким образом мода случайной величины равна такому её значению, при котором:

(6.2)