На рис.6.2 показана мода непрерывной унимодальной (с одной модой) случайной величины, заданной плотностью распределения.
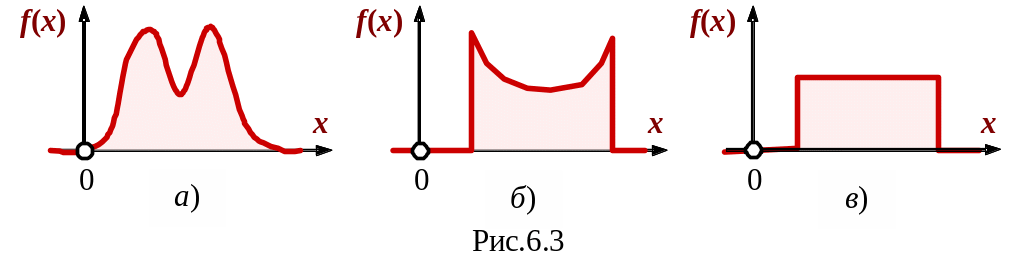
Кроме унимодальных распределений случайных величин, различают полимодальные (рис.6.3,а), антимодальные (рис.6.3,б) и безмодальные (рис.6.3,в).
1. 3. Медиана
Определение 6.3.
Медианой
называют
такое значение Ме
случайной
величины, для которого справедливо
равенство
.
Перпендикуляр к числовой оси, проходящий через медиану, делит площадь, ограниченную графиком плотности распределения f(x) и числовой осью x, на две равные части (рис.6.4).
Для симметричного унимодального закона распределения случайной величины значения математического ожидания, моды и медианы совпадают.
2. Моменты случайных величин. Для характеристики различных свойств случайных величин используются начальные и центральные моменты.
Определение 6.4.
Начальным
моментом
k-го
порядка
называют
математическое ожидание k–ой
степени случайной величины
.
(6.3)
(6.4)
Определение 6.5.
Отклонение случайной
величины от математического ожидания
называют
центрированной
случайной величиной
.
(6.5)
Определение 6.6.
Центральным
моментом s-го
порядка называют
математическое ожидание s
– ой
степени
центрированной случайной величины
. (6.6)
(6.7)
3. Свойства моментов случайных величин. Особого внимания заслуживают свойства начальных и центральных моментов первого и второго порядков.
Свойство 1
Первый начальный момент (начальный момент 1-го порядка) α1 представляет собой математическое ожидание случайной величины:
α1 = М[X1] = mx . (6.8)
Свойство 2
Первый центральный момент μ1 любой случайной величины равен нулю.
.
Первый центральный момент на практике не используется, поскольку ничего характеризовать не может.
Свойство 3
Второй начальный момент α2 характеризует степень разброса случайной величины вокруг ее математического ожидания, а также смещение случайной величины на числовой оси относительно начала координат.
.
(6.9)
В силу того, что второй начальный момент характеризует сразу два свойства случайной величины, он как самостоятельная числовая характеристика не используется.
Свойство 4
Второй центральный момент μ2 называется дисперсией D(X) и характеризует степень разброса случайной величины вокруг ее математического ожидания.
(6.10)
Дисперсия имеет размерность квадрата случайной величины.
На рис.6.5 показаны две непрерывные случайные величины, заданные в виде плотности распределения c одинаковыми математическими ожиданиями (mх2 = mх1) и отличающиеся друг от друга своей дисперсией (Dх2 > Dх1).
Определение дисперсии Dx для непрерывных случайных величин связано с трудоемкими вычислениями определенных интегралов. На практике дисперсию вычисляют с помощью второго начального момента α2 и математического ожидания (первого начального момента) mх.
Таким образом
.
(6.11)
(6.12)
Свойство 5
Среднее квадратичное отклонение представляет собой квадратный корень из дисперсии
(6.13)
Ошибка измерения представляет собой среднее квадратичное отклонение измеренной величины.
Лекция № 7
Законы распределения случайных величин
1. Законы распределения дискретных случайных величин.
Из всего многообразия дискретных случайных величин выделяют две большие группы: биномиальные величины и пуассоновские. В связи с этим особый интерес представляют собой биномиальный и пуассоновский законы распределения дискретных случайных величин.
1.1. Биномиальный закон распределения
Пусть производится n независимых опытов, в каждом из которых с одинаковой вероятностью р может произойти некоторое событие А. Случайная величина Х – число опытов, в которых произошло событие А – распределена по биномиальному закону распределения
(7.1)
с рядом распределения
xi |
0 |
1 |
. . . |
m |
. . . |
n |
pi |
(1-p)n |
np(1-p)n-1 |
. . . |
Cnm pm(1-p)n-m |
. . . |
pn |
Где
=
1.
Для доказательства данного факта следует сумму рассматривать как разложения бинома Ньютона с переменными р и (1-р), т.е.
= [ p + (1 – p) ]n = 1 .
Биномиальный закон распределения имеет два параметра:
р – вероятность появления событие А в одном опыте;
n – общее число опытов (испытаний).
Вероятность попадания дискретной случайной величины, распределенной по биномиальному закону, в заданный диапазон значений определяется с помощью формулы
(7.2)
Числовые характеристики биномиальной случайной величины