Если участок [α,β] не входит в диапазон [a,b], то выражение (7.17) не является справедливым. В этом случае необходимо руководствоваться выражением если (7.18)

где – длина участка на числовой оси, являющегося пересечением для участка [α,β] и диапазона [a,b] .

Задача 7.3.

НСВ Х – равномерно распределенная на отрезке [3,8]. Найти P{6  X  7}.

2.2. Показательный закон распределения

В простейшем потоке событий случайная величина Х – интервал времени между двумя последовательными событиями распределена по показательному закону.

Определение 7.7.

Непрерывная случайная величина распределена по показательному закону, если ее плотность распределения имеет вид:

(7.19)

где λ – интенсивность событий, т.е. количество событий в единицу времени.

График плотности распределения для случайной величины, распределенной по показательному закону, имеет вид, показанный на рис.7.4

Показательный закон распределения имеет только один параметр λ .

Интегральная функция распределения определяется следующим образом:

Таким образом, интегральная функция случайной величины, распределенной по показательному закону, определяется выражением

(7.20)

График интегральной функции (5.19) изображен на рис.7.5.

Числовые характеристики

1. Математическое ожидание.

(7.21)

Доказательство.

В соответствии с формулой (6. ) математическое ожидание случайной величины, распределенной по показательному закону, определяется следующим образом:

Проинтегрируем полученный интеграл по частям.

,

т.е.

Примечание. Вычисление предела осуществляется по правилу Лопиталя.

2. Дисперсия.

Полученный интеграл проинтегрируем по частям. Обозначим: , тогда . Проинтегрируем по частям:

Дисперсию определим по формуле связи:

т.е. (7.22)

3. Среднее квадратичное отклонение.

(7.23)

4. Вероятность попадания случайной величины на заданный участок

Вероятность попадания случайной величины на заданный участок [a,b], если участок входит в диапазон [0, ], можно определить двумя способами:

1-й способ.

.

2-й способ.

.

Таким образом,

(7.24)

Геометрически вероятности соответствует область, выделенная штриховкой на рис.7.5.

2.3. Нормальный закон распределения

Наиболее простым и достаточно точно отражающим случайные ошибки измерений является так называемый нормальный закон распределения.

Определение 7.8.

Непрерывная случайная величина распределена по нормальному закону, если ее плотность распределения имеет вид:

(7.25)

где σ и m – параметры распределения.

График плотности распределения для случайной величины, распределенной по нормальному закону, имеет вид, показанный на рис.7.6.

Интегральная функция распределения определяется следующим образом:

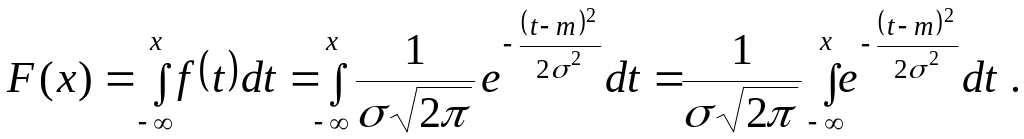
Таким образом, интегральная функция случайной величины, распределенной по нормальному закону, определяется интегралом

(7.26)

График интегральной функции изображен на рис.7.7.

Числовые характеристики