1. Математическое ожидание.
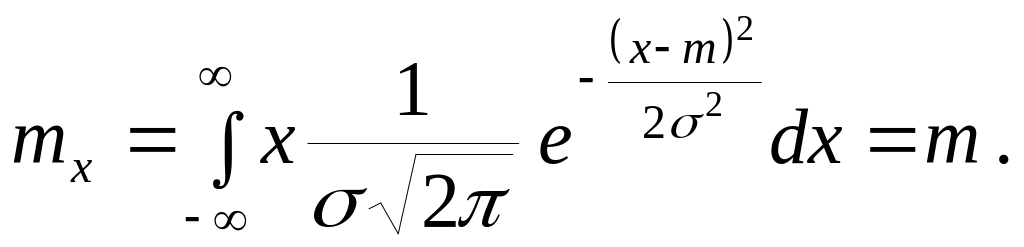(7.27)
2. Дисперсия.
(7.28)
3. Среднее квадратичное отклонение.
(7.29)
Центральные моменты.
Центральные моменты любого порядка нормально распределенной случайной величины определяется рекуррентным соотношением
(7.30)
Зная 1-й и 2-й центральные моменты, можно легко найти любой другой.
Поскольку 1-й центральный момент для всех случайных величин равен нулю, то все центральные нечетные моменты для нормально распределенной случайной величины также равны нулю.
Поскольку 2-й центральный момент
то все четные центральные моменты нормально распределенной случайной величины легко определяются с помощью выражения (5.29):
Поскольку все нечетные центральные моменты для нормально распределенной случайной величины равны нулю, то коэффициент асимметрии также равен нулю:
Коэффициент островершинности (величина эксцесс) для нормально распределенной случайной величины также равен нулю:
4. Вероятность попадания случайной величины на заданный участок
Вероятность попадания нормально распределенной случайной величины на заданный участок[a,b] можно получить по известным формулам:
Однако в этом случае интегрирование надо проводить численными методами.
Чтобы избежать сложностей при вычислениях функция распределенной случайной величины Х может быть выражена через частную интегральную функцию Лапласа
(7.30)
т.е. интегральную функцию нормально распределенной случайной величины с параметрами: m = 0; σ = 1. Распределение (7.30) называют стандартным нормальным распределением.
Интегральная функция F(x) нормально распределенной случайной величины связана со стандартной интегральной функцией соотношением
Тогда вероятность попадания случайной величины на заданный участок
(7.31)
На рис.7.8 изображена интегральная функция стандартного нормального распределения (сравни с рис.5.6)
Рассмотрим F*(x) от аргумента x > 0
0
,
где Ф(х) – функция Лапласа (см. Приложение В).
Поскольку то (7.31) перепишется как
т.е.
(7.32)
Формула (7.32) обладает высокой универсальностью, поскольку позволяет определять вероятность попадания на заданный участок любой нормально распределенной случайной величины независимо от значений её параметров m и σ.
3. Правило трех сигм
Формула (7.32) может быть использована для вычисления вероятности того, что отклонение случайной величины X, распределенной по нормальному закону от её математического ожидания по абсолютной величине меньше заданного числа . Часто такой расчет требуется в практических задачах, т.е. когда требуется найти вероятность осуществления неравенства
(7.33)
Преобразуем (7.33) в
(7.34)
и подставим в формулу (7.32). Поскольку Ф(х) нечетная функция, т.е. Ф(–х) = –Ф(х), имеем:
т.е. вероятность модуля отклонения случайной величины, распределенной по нормальному закону, можно вычислить по формуле:
(7.35)
Если измерять величину отклонения в единицах , то можно вывести практически полезную закономерность, которая известна как правило трех сигм. Действительно, положим в (5.35) =t. Получим:
Если t=3 и, следовательно, t = 3, то
т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднеквадратичного отклонения, очень велика. Это означает, что вероятность противоположного события, которое заключается в том, что абсолютное отклонение превысит утроенное , очень мала, а именно равна 0,0027. В этом и состоит сущность правила трех сигм.
Правило трех сигм.
Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднеквадратичного отклонения.