- •Введение
- •Литература
- •Элементы теории вероятностей
- •Случайное событие и вероятность
- •Определение вероятности
- •Принцип практической невозможности маловероятных событий
- •Формулы комбинаторики
- •Условная вероятность
- •Независимые события
- •Свойства вероятности
- •Формула полной вероятности
- •Формула Байеса
- •Случайная величина
- •Свойства математического ожидания
- •Дисперсия дискретной с.В.
- •Свойства дисперсии
- •Закон больших чисел.
- •Функция распределения случайной величины
- •Свойства функции распределения
- •Односторонние и двухсторонние значения вероятностей
- •Нормальное распределение
- •Взаимосвязи случайных величин Парная корреляция
- •Элементы математической статистики
- •Генеральная и выборочная совокупность
- •Основные шкалы измерений
- •Точечные оценки параметров распределения
- •Проверка статистических гипотез
- •Исследование зависимости между двумя характеристиками
- •Лабораторная работа Задание 1. Нахождение выборочных характеристик
- •Задача 1.1.
- •Задача 1.2.
- •Задача 1.3.
- •Задача 1.4.
- •Задача 1.5.
- •Задача 1.6.
- •Задание 2 Построение гистограммы выборки
- •Задача 2.1
- •Задание 3 Проверка статистических гипотез
- •Одновыборочный критерий Стьюдента
- •Двухвыборочный критерий Стьюдента
- •Критерий согласия хи-квадрат
- •Задание 4. Интервальные оценки
- •Задача 4.1.
- •Задача 4.2.
- •Анализ значения коэффициента корреляции
- •Построение линий регрессии
- •Преподавателю и студенту было предложено расположить 15 профессий в порядке их восстребованности на рынке. В результате получилась следующая таблица:
- •Оглавление
Функция распределения случайной величины
При
статистических исследованиях приходится
рассчитывать вероятности определенных
событий. При этом классическая модель
определения вероятности мало подходит,
поскольку область значений с.в. заранее
не задана, и может меняться в достаточно
широких пределах. Поэтому для расчетов
используют непрерывные случайные
величины. Как уже упоминалось выше, для
описания дискретной случайной величины
достаточно задать вероятность каждого
его значения:
![]() .
Однако в случае случайных величин,
принимающих бесконечное множество
значений, такой подход неприемлем.
Рассмотрим определение функции
распределения с.в., которое обобщает
оба случая:
.
Однако в случае случайных величин,
принимающих бесконечное множество
значений, такой подход неприемлем.
Рассмотрим определение функции
распределения с.в., которое обобщает
оба случая:
Функцией распределения
с.в. Х называют функцию
![]() ,
определяющую вероятность того, что с.в.
Х в результате испытания примет значение
меньше
,
определяющую вероятность того, что с.в.
Х в результате испытания примет значение
меньше
![]() ,
т.е.
,
т.е.
![]() .
Другими словами, распределение числовой
случайной величины – это функция,
которая однозначно определяет вероятность
того, что случайная величина принимает
заданное значение или принадлежит к
некоторому заданному интервалу.
Используемые в вероятностно-статистических
методах принятия решений и других
прикладных исследованиях функции
распределения бывают либо дискретными,
либо непрерывными, либо их комбинациями.
.
Другими словами, распределение числовой
случайной величины – это функция,
которая однозначно определяет вероятность
того, что случайная величина принимает
заданное значение или принадлежит к
некоторому заданному интервалу.
Используемые в вероятностно-статистических
методах принятия решений и других
прикладных исследованиях функции
распределения бывают либо дискретными,
либо непрерывными, либо их комбинациями.
1.
Случайная величина принимает конечное
число значений. Упорядочим значения
с.в. по неубыванию:
![]() .
.
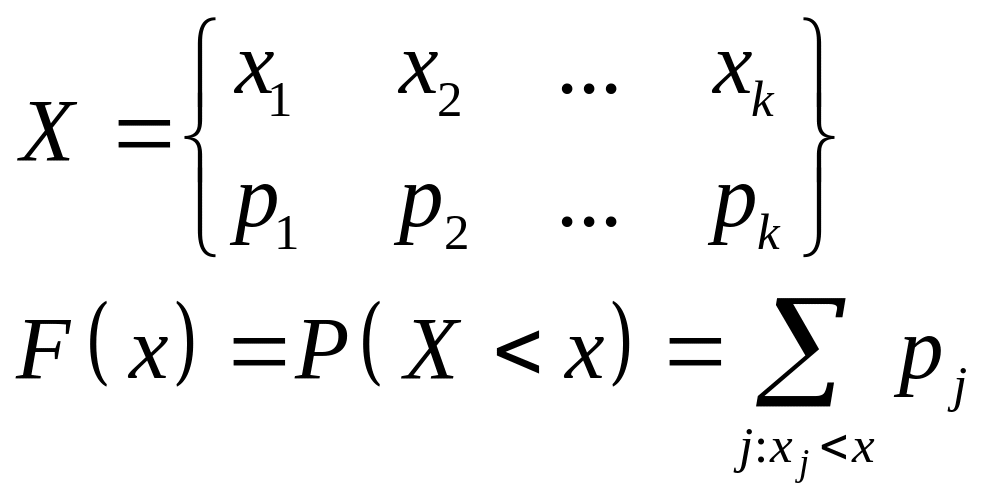
График функции распределения случайной величины Х выглядит следующим образом:
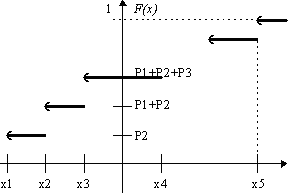
2. Случайная величина
является непрерывной и принимает
бесконечно много значений. Это возможно
лишь тогда, когда вероятностное
пространство, на котором определена
случайная величина, состоит из бесконечного
числа элементарных событий. Для
непрерывных с.в. бессмысленно задавать
вероятности
![]() ,
поскольку они все равны нулю. Поэтому
рассматриваются вероятности
,
поскольку они все равны нулю. Поэтому
рассматриваются вероятности
![]() принадлежности значений случайной
величины интервалу
принадлежности значений случайной
величины интервалу
![]() .
Можно показать, что
.
Можно показать, что
![]() .
В этом случае мы имеем неубывающую
непрерывную функцию распределения.
Используемые в статистике непрерывные
функции распределения, как правило,
имеют производные. Первая производная
.
В этом случае мы имеем неубывающую
непрерывную функцию распределения.
Используемые в статистике непрерывные
функции распределения, как правило,
имеют производные. Первая производная
![]() функции распределения
функции распределения
![]() называется функцией плотности вероятности.
По плотности вероятности можно определить
функцию распределения посредством
соотношения
называется функцией плотности вероятности.
По плотности вероятности можно определить
функцию распределения посредством
соотношения
![]() .
Из соотношений
.
Из соотношений
![]() и
и
![]() следует
следует
![]() .
При этом вероятность
определяется по формуле
.
При этом вероятность
определяется по формуле
![]() .
.
График плотности
вероятностей называют кривой распределения.
Вероятность
попадания случайной величины в интервал
![]() численно равна площади криволинейной
трапеции, ограниченной сверху графиком
функции
численно равна площади криволинейной
трапеции, ограниченной сверху графиком
функции
![]() и с основанием
,
т.е. графически вероятность изображается
как площадь под кривой, ограниченной
пределами значений переменной
и с основанием
,
т.е. графически вероятность изображается
как площадь под кривой, ограниченной
пределами значений переменной

А вся площадь под кривой распределения равна единице.
Пример 2. Рассмотрим следующую функцию распределения:
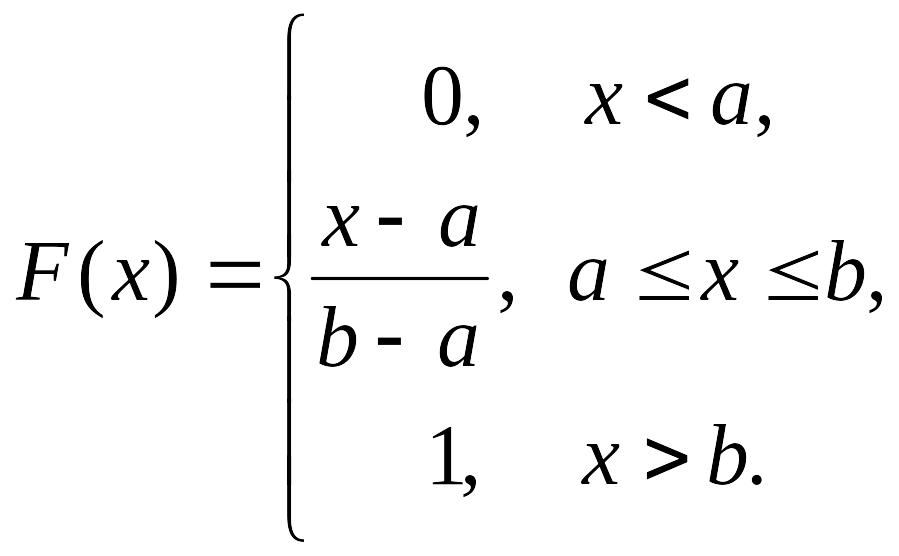
где a и b – некоторые числа, a<b. Ниже на рисунке приведен график этой функции
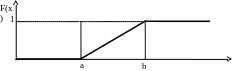
Беря производные, найдем плотность вероятности этой функции распределения:
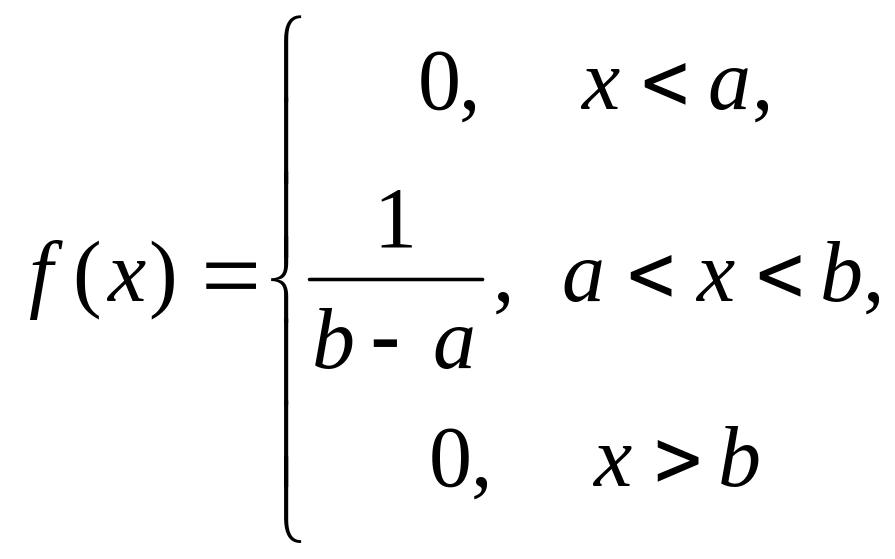
(в точках x = a и x = b производная функции F(x) не существует). Заданная функция определяет функцию равномерного распределения на отрезке . график плотности этой случайной величины приведен на рисунке