Формула полной вероятности

П усть имеется полная группа событий и для каждого из событий известна вероятность наступления этого события, . Пусть А – некоторое событие, которое может наступить при выполнении одного из событий ; известны условные вероятности , . Необходимо найти .

Из определения следует, что все события, составляющие полную группу, попарно несовместны: ; их объединение образует пространство элементарных исходов . В этом случае событие (см. рисунок) как бы разбивается на части, и подсчитывается средняя вероятность выполнения в зависимости от выполнения одного из событий :

Приведенная формула называется формулой полной вероятности.

Пример 1.20. Студент перед зачетом выучил 20 вопросов из 25. Каждый билет содержит ровно один вопрос из программы. Каким по порядку (первым или вторым) лучше сдавать зачет, при условии, что каждый студент может отвечать только по одному выбранному билету, и каждый билет может быть выбран студентами ровно один раз(выбранный билет обратно не возвращается)?

Решение: Имеем две стратегии сдачи зачета. Обозначим через - событие, что студент выбирает счастливый билет. Тогда, при условии, что студент сдает зачет первым .

При условии, что студент сдает зачет вторым по порядку, возможны следующие события: - студент, сдававший первым, взял билет с вопросом, который наш студент не знает, и - был взят билет с вопросом, который наш студент знает. Тогда и . Несложно подсчитать, что и . По формуле полной вероятности получим

⁵

Формула Байеса

Пусть событие может наступить при условии появления одного из несовместных событий , которые образуют полную группу событий. Поскольку неизвестно какое из этих событий наступит, их называют гипотезами. Вероятность события определяется по формуле полной вероятности

При условии, что событие произошло, можно вычислить вероятности событий . Имеет место формула Байеса

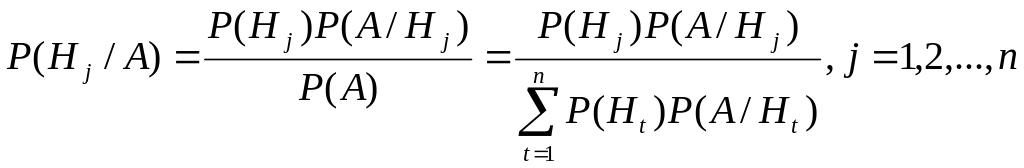
Вероятности , называются априорными (“a priori” – до опыта), вероятности - называются апостериорными (“a posteriopri” – после опыта). При справедливости гипотезы вероятность наступления события равна . Если в результате опыта событие наступило, то можно уточнить вероятности гипотез по указанной формуле.

Пример 1.21.⁶ Пусть известно, что преступление могло быть совершено ровно одним из двух подозреваемых лиц (события и ); вероятность совершения преступления первым лицом равно , соответственно вторым лицом - . При проведении следственного эксперимента (событие ), обнаружилось, что некоторый факт мог иметь место с вероятностью 0.6, если преступником было первое лицо, и - с вероятностью 0.98 при условии, что преступник – второе лицо. Можно ли говорить о том, что следственный эксперимент подтвердил или опроверг исходные посылки?

Решение: Мы находимся в условиях формулы Байеса. Имеем: , , , . По формуле Байеса

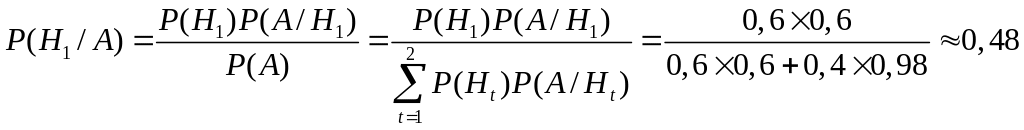
Как мы видим, следственный эксперимент в небольшой степени снял подозрения с первого лица.

Случайная величина

При применении методов теории вероятностей исследователь чаще всего имеет дело с числовыми характеристиками наблюдаемого объекта, которые являются функциями элементарных исходов состояния объекта. Случайной называют числовую функцию⁷, которая определена на множестве элементарных исходов. Примерами случайных величин являются:

4.1. Число родившихся мальчиков среди двухсот новорожденных является случайной величиной, принимающей значения от 0 до 200.

4.2. Число преступлений совершаемых за определенный период в некотором мегаполисе является случайной величиной, для значения которой мы можем дать только нижнюю оценку (значения ограничены снизу нулем).

4.3. Температура человеческого тела является также случайной величиной с бесконечным множеством значений.

4.4. Симметричная монета подбрасывается 3 раза. Число выпавших гербов является случайной величиной, которая принимает значения 0,1,2,3.

Дискретной называют случайную величину (с.в.), которая принимает отдельные изолированные значения с определенными вероятностями. Число возможных значений с.в. может быть конечным или бесконечным (примеры 4.1 и 4.2.).

Непрерывной называют случайную величину, которая принимает все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной с.в. бесконечно (пример 4.3).

Для задания с.в. необходимо перечислить множество ее значений с указанием вероятностей этих значений. Законом распределения дискретной с.в. называют соответствие между возможными значениями и их вероятностями. При табличном задании с.в. получаем

:

: ,

где набор образует распределение вероятностей с.в. . Поскольку с.в. может принимать значения только из множества , то .

Распределение случайной величины можно задать различными способами:

• в виде таблицы значений величины и соответствующих им вероятностей

• в виде формулы:

• в виде диаграммы:

Рассмотрим пример 4.4.

При трехкратном подбрасывании симметричной монеты и анализе возможных результатов эксперимента мы имеем 8 элементарных событий, которые приведены в таблице

1 бросок	2 бросок	3 бросок	число гербов	вероятность
Р	Р	Р	0	1/8
Р	Р	Г	1	1/8
Р	Г	Р	1	1/8
Р	Г	Г	2	1/8
Г	Р	Р	1	1/8
Г	Р	Г	2	1/8
Г	Г	Р	2	1/8
Г	Г	Г	3	1/8

Интересующая нас случайная величина задается в виде таблицы

Число гербов	0	1	2	3
Вероятность	0,125	0,375	0,375	0,125

Для той же самой случайной величины распределение вероятностей может быть описано в виде формулы. Обозначим через - вероятность появления герба при однократном подбрасывании монеты, через - вероятность выпадения гербов при - кратном подбрасывании монеты. Тогда ⁸, , где - число способов выбора гербов из монет. Легко проверить, что при мы получаем распределение вероятностей из вышеприведенной таблицы.

Третий вариант задания распределения случайной величины является графическим. Случайная величина задается специальным графиком (гистограммой). Гистограмма строится таким образом, что площадь каждого прямоугольника при равных основаниях была пропорциональна вероятностям распределения данной с.в.

Ниже приведен пример гистограммы распределения нашей случайной величины

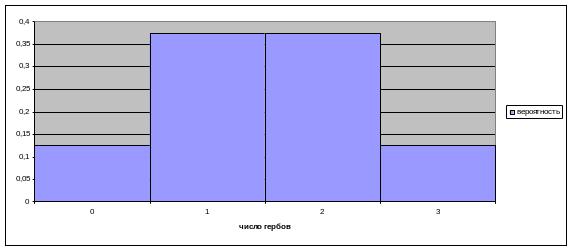
Случайные величины и , определенные на одном и том же пространстве элементарных событий, называются независимыми, если для любых значений а и b независимы события {X=a} и {Y=b}. Другими словами для любых значений а и b выполняется .

Математическое ожидание дискретной с.в.

Математическим ожиданием случайной величины X называется число вида

где – -е значение случайной величины, а - вероятность принятия этого значения. Заметим, что если в формуле математического ожидания принять все вероятности равными 1/n, получается формула вычисления среднего арифметического чисел .

Пример 1.22: Найти математическое ожидание числа появлений события в одном испытании, если вероятность этого события равна р.

Решение. Построим случайную величину , принимающую значение 1, если событие происходит, и принимающую значение 0 в противном случае. Тогда .

Таким образом, математическое ожидание числа появлений события в одном испытании равно вероятности этого события.

Пример 1.23: Найти математическое ожидание для случайной величины, описанной в примере 4.4.

Решение. Используя таблицу описания случайной величины, имеем

Смысл математического ожидания заключается в следующем: это точка на числовой оси, относительно которой группируются результаты конкретных испытаний над случайной величиной, она приближенно равна среднему арифметическому числа наблюдаемых значений случайной величины (некоторое подобие центра тяжести в механике).