Принцип практической невозможности маловероятных событий

Особую роль в статистических исследованиях играют практически невозможные (и сопутствующие им практически достоверные) события. Ни один прогноз в области случайных явлений не является и не может являться полностью достоверным; он может быть только практически достоверным, т. е. осуществляться с очень большой вероятностью. В основе применения всех выводов и рекомендаций, добываемых с помощью теории вероятностей, лежит принцип практической уверенности, который можно сформулировать следующим образом:

Если вероятность события А в данном опыте весьма мала, то (при однократном выполнении опыта) можно вести себя так, как будто событие А вообще невозможно, т. е. не рассчитывать на его появление.

В повседневной жизни мы постоянно (хотя и бессознательно) пользуемся этим принципом. Например, выезжая куда-то на поезде, мы не рассчитываем на возможность погибнуть в дорожной катастрофе, хотя некоторая (весьма малая) вероятность этого события все же имеется.

Насколько маленькой должна быть вероятность события, чтобы это событие можно было считать практически невозможным? Ответ на этот вопрос выходит за рамки математической теории и в каждом отдельном случае решается из практических соображений в зависимости от сферы приложений полученных результатов. Чем более опасными являются последствия возможной ошибки предсказания, тем ближе к нулю должна быть вероятность события, чтобы его считать практически невозможным. Например, заложенная в проекте строительства атомной станции, вероятность 0,01 того, что здание не разрушится при природных катаклизмах, считается абсолютно недопустимой, но такая же вероятность ошибки при прогнозировании погоды может считаться приемлемой. Остаточно малую вероятность, при которой (применительно к данной определенной задаче) событие можно считать практически невозможным, называют уровнем значимости. На практике уровень значимости обычно заключен между 0,01 и 0,05.

Формулы комбинаторики

Для подсчета вероятности события с использованием классической схемы необходимо уметь определять число всех событий, составляющих пространство элементарных событий, а также число элементарных событий, составляющих событие . Для вычисления этих показателей часто используют формулы комбинаторики. Комбинаторика, - раздел математики, посвященный решению задач построения и подсчета числа конфигураций элементов некоторого, обычно конечного, множества, в соответствии с заданными правилами. Каждое такое правило определяет способ построения некоторой конструкции из элементов исходного множества. Примерами комбинаторных конфигураций являются перестановки, размещения и сочетания

Набор элементов из –элементного множества называется выборкой объема из элементов или -выборкой. Выборка называется упорядоченной, если зафиксирован порядок следования элементов в ней. Две упорядоченные выборки, различающиеся лишь порядком следования элементов (выборки (1,3,5) и (5,1,3)), считаются различными. Если порядок следования элементов не является существенным, то выборка называется неупорядоченной. В выборках могут допускаться или не допускаться повторения элементов из основного набора.

Упорядоченные -выборки при возможности повтора элементов называют размещениями с повторениями из элементов по или -размещениями с повторениями, а их число обозначают символом .

Если элементы упорядоченной -выборки попарно различны, то ее называют размещением из элементов по без повторений или -размещением без повторений. Количество -размещений без повторений будем обозначать через .

Неупорядоченная -выборка, в которой элементы могут повторяться, называется сочетанием с повторениями из элементов по или, короче, -сочетанием с повторениями, а число -сочетаний с повторением обозначают символом .

Если элементы неупорядоченной выборки попарно различны, она называется сочетанием (без повторений) из элементов по или -сочетанием. Каждое такое сочетание представляет собой подмножество мощности множества . Число сочетаний из элементов по будет обозначаться через .

Пример 1.5. Пусть и необходимо построить выборку из 2 элементов, . Тогда имеются:

• девять размещений с повторениями – ;

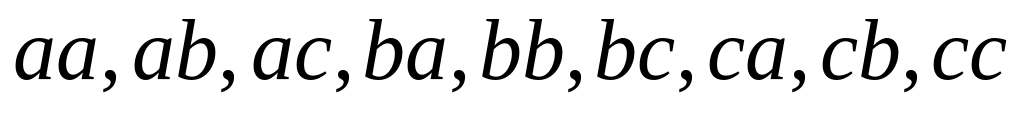• шесть размещений без повторений – ;

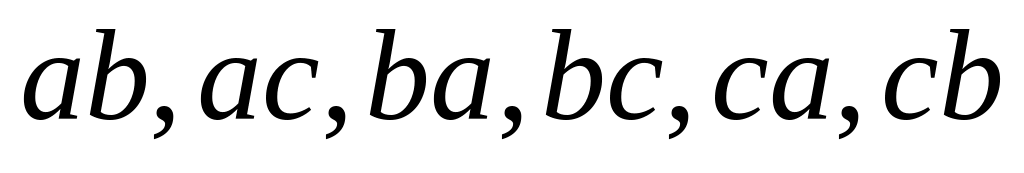• шесть сочетаний с повторениями – ;

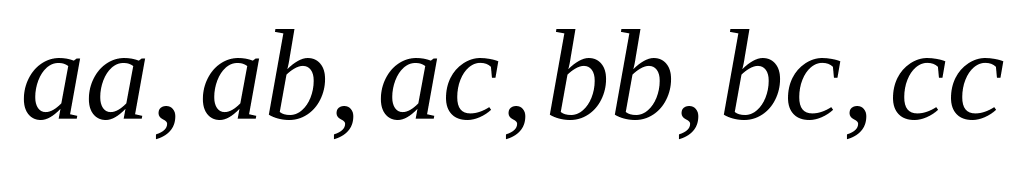• три сочетаний без повторений – .

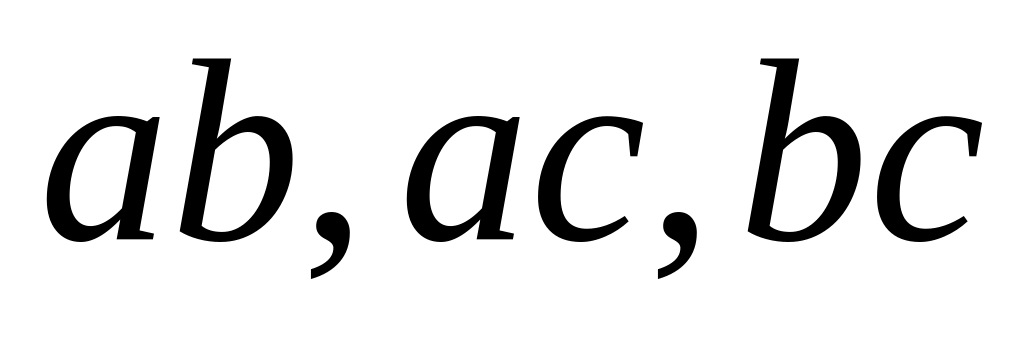В первом случае, перечисляются всевозможные пары элементов из множества . Удаление из списка пар с повторяющимися значениями приводит ко второму случаю, третий случай содержит только пары с точностью до перестановки элементов, удаление из третьего списка пар с повторяющимися элементами дает четвертый список.

Фундаментальную роль в решении перечислительных задач комбинаторики играют правило суммы и правило произведения:

Правило суммы заключается в следующем: Если существует разбиение множества изучаемых комбинаций на классы (каждая комбинация содержится ровно в одном классе), то общее число комбинаций равно сумме комбинаций, входящих в каждый из классов.

При наличии 2 классов правило суммы можно интерпретировать так: если объект может быть выбран способами, а объект – другими способами при условии, что одновременный выбор и невозможен, то выбор « или » можно осуществить способами.

Правило произведения можно сформулировать следующим способом: Если объект типа можно выбрать способами, и после такого выбора объект можно выбрать способами, то выбор пары можно осуществить способами.

Пример 1.6. Пусть имеется схема дорожного сообщения между населенными пунктами и . Часть дорог проходит через населенный пункт (3 дороги соединяют и , 4 дороги - и ), а часть через (5 дорог соединяют и , 2 дороги - и ). Необходимо подсчитать число различных способов проезда от к при условии, что каждый населенный пункт посещается не более одного раза.

Решение. Разобьем множество всех вариантов на два подмножества: - множество дорог, ведущее от к через пункт , соответственно - множество дорог, ведущее от к через пункт . Тогда по правилу сложения необходимо найти решения з адачи для случаев и с последующим суммированием результатов. Поскольку для каждого выбора дороги из в существует 4 выбора продолжения пути из в , то число решений задачи равно 3*4=12(правило умножения). Полное решение задачи описывается формулой 3*4+5*2=22.

Пример 1.7. Посчитать число двоичных последовательностей длины

Решение: Каждый элемент последовательности может независимо от окружения принимать одно из двух значений 0 или 1. Применяя правило произведения, и учитывая длину последовательности, получаем, что число последовательностей равно произведению двоек или .

Обозначим через произведение всех целых чисел от 1 до . Положим . Приведем без доказательства следующий результат:

Теорема. Пусть производится выборка элементов из множества содержащего элементов. В зависимости от типа выборки имеем

1)

2)

3)

4)

Пример 1.8. Пассажир забыл пароль камеры хранения на вокзале. Каково максимальное число вариантов необходимо перебрать, если пароль содержит 5 символов, набираемых в алфавите из 32 символов?

Решение: При наборе каждого символа последовательности открывающей код камеры необходимо сделать выбор из 32 символов алфавита. Всего отбирается 5 символов, причем один и тот же символ может встречаться в набираемой последовательности многократно. При этом порядок следования символов в пароле важен. Имеем случай размещений с повторениями с параметрами . Тогда .

Пример 1.9. Сколько существует способов рассадить на опознании группу из 6 человек в ряд вдоль стены?

Решение: Имеется 6 мест, на которые необходимо рассадить 6 человек. Ни один человек не может одновременно занимать два места. Из условия задачи следует, что порядок выбора существенен. Имеем схему размещений без повторений с параметрами: . Поэтому количество вариантов равно

Пример 1.10. Сколько существует способов отобрать 4-х студентов на сельхоз-работы из группы 9 студентов?

Решение: Из условия задачи следует, что важно назвать отобранных студентов, а порядок отбора не важен, кроме того, один и тот же студент не может быть отобран более одного раза. Имеем схему без повторений, порядок следования не важен. Тогда ответ задачи в соответствии с теоремой описывается числом:

Пример 1.11. Сколько существует способов разделить наследство в 100 рублей с точностью до рубля между 10 наследниками?

Решение: Расположим 100 рублей по рублю в ряд, и проставим 9 меток между ними. Выбор меток определяет распределение наследства суммы между наследниками. Сумма, которая находится левее первой метки, достанется первому наследнику, между первой и второй – второму, и т.д. Все, что лежит правее последней девятой метки, отходит 10 наследнику. При совпадении двух меток, соответствующий наследник ничего не получает. Поэтому наследодателю необходимо определить положения 9 меток (метки повторяются, поэтому имеем повторную выборку) между 100 позициями (учитывая расположение меток, всего позиций - 109), порядок выбора меток несущественен. Имеем неупорядоченную -выборку, в которой элементы могут повторяться. Ответ определяется выражением , которое является достаточно большим числом и здесь не приводится.

Разберем несколько примеров подсчета вероятности по формуле (1) .

Пример 1.12. В коробке шесть одинаковых занумерованных кубиков. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.

Решение: Обозначим через - событие, что кубики выбраны в порядке возрастания их номеров. Поскольку извлеченный кубик не возвращается в коробку, то общее число вариантов равно . Комбинация, составляющая событие А, имеется в единственном виде ( ). Следовательно, .

Пример 1.13. В группе 12 студентов, из них 5 отличников. По списку, наудачу, отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов – три отличника.

Решение: Возможность числа вариантов выбора 9 студентов из 12 описывается формулой . Это число составляет значение для нашей задачи. Для того чтобы найти необходимо подсчитать число вариантов, при которых в отобранную группу входит 3 отличника. Поскольку этих отличников можно выбирать только из 5 человек, то число таких вариантов равно . Оставшиеся шесть места заполняются не отличниками (возможных кандидатов - 7). Общее число вариантов выбора равно . Используя правило произведения, получим . Тогда, .