Условная вероятность

У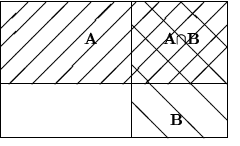 словной вероятностью события A при условии, что произошло событие B, называется величина

Условную вероятность определяется лишь для событий B, вероятность которых не равна нулю.

Пример 1.14. Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом вероятность того, что выпало четное число очков?

Решение: Обозначим через событие выпадения более 3 очков. Тогда . Событию (выпало четное число очков) благоприятствуют два из них: . Поэтому, .

Другое решение задачи получается с использованием формулы, определяющей условную вероятность. Мы хотим вычислить отношение числа исходов, благоприятствующих внутри (то есть благоприятствующих одновременно и ), к числу исходов, благоприятствующих  .

Из вышесказанного следует, что . В общем виде, предыдущее соотношение выглядит следующим образом:

Независимые события

Важным понятием теории вероятностей является независимость. События A и B называются независимыми, если . Тогда

т.е. вероятность одновременного осуществления этих событий равна произведению их вероятностей. Легко видеть, что и . Независимость одного события от другого означает, что осуществление одного из них никак не влияет на результат другого события.

Пример 1.15. Найти вероятность совместного поражения цели двумя стрелками, если вероятность поражения цели первым стрелком равна 0,7, а вторым – 0,6.

Решение: При одновременной стрельбе по цели двух стрелков событие поражения цели первым стрелком и событие поражения цели вторым стрелком являются независимыми. При условии, что и вероятность их совместного попадания равна .

Отметим, что если независимы события и , то независимы и события и , и , и .

События называются попарно независимыми, если любая пара из них является парой независимых событий

События называются независимыми в совокупности, если вероятность одновременного осуществления любого конечного поднабора из них равна произведению вероятностей событий этого поднабора.

Независимые в совокупности события независимы и попарно. Обратное неверно.

Пример 1.16. Являются ли зависимыми события извлечь из колоды, содержащей 32 карты – туза и карту червовой масти?

Решение: Из колоды карт в 32 листа извлекается одна карта. Пусть А – событие, состоящее в том, что извлечённая карта – туз. Событие В состоит в том, что извлечённая карта червовой масти. Очевидно, что Р(А)=4/32=1/8, и Р(В)=8/32. Поскольку вероятность извлечения из колоды червового туза равна , то из соотношения следует, что события А и В независимы.

Свойства вероятности

1. вероятность принадлежит интервалу [0,1]. Вероятность достоверного события равна 1, невозможного события – равна нулю , ,

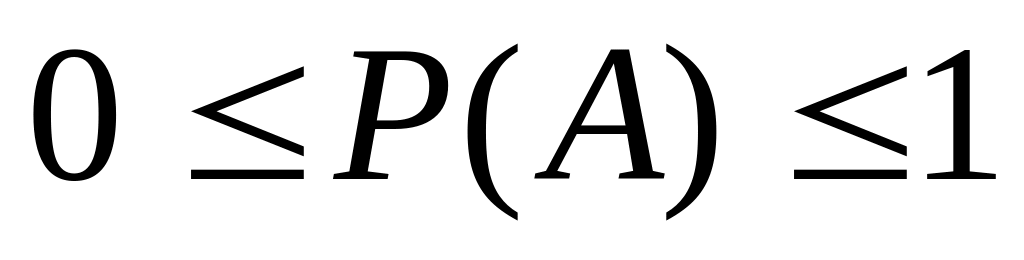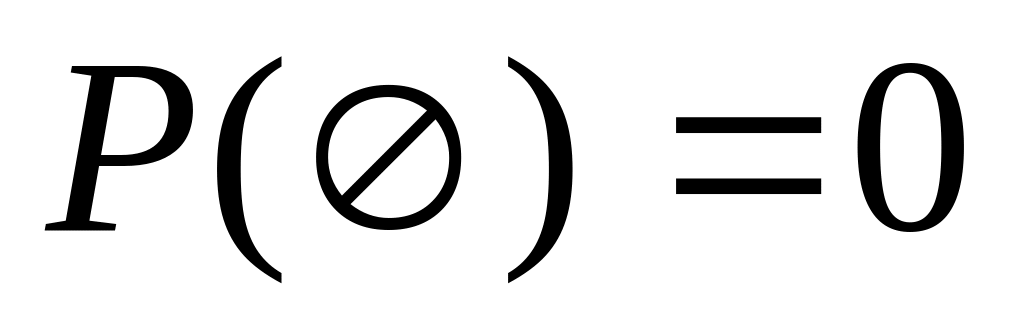
2. сумма вероятностей некоторого события и его дополнения равна 1

3. свойство монотонности вероятности

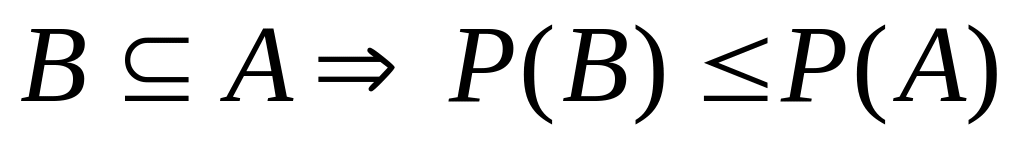
4. вероятность объединения событий:

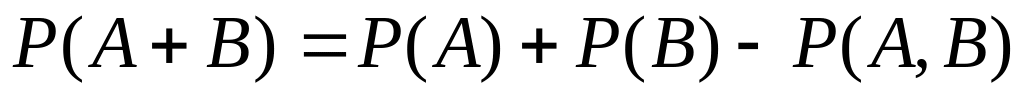
Пример 1.17. Два стрелка сделали по одному выстрелу. Найти вероятность поражения цели ровно одним стрелком в тире, если вероятность попадания первого стрелка 0,6, а второго – 0,7.

Решение: Обозначая через А – событие: попадание первого стрелка, через В – соответственно для второго стрелка, учитывая независимость событий, будем иметь, что искомая вероятность складывается из вероятностей двух событий:

- попал первый стрелок, второй – промахнулся;

- попал второй стрелок, первый – промахнулся;

Тогда,

Пример 1.18. Найти вероятность вытащить туза или червовую масть при случайном отборе одной карты из колоды в 32 листа.

Решение: Поскольку колода содержит по 4 карты одинакового ранга и по восемь карт одной масти, имеем

Р(ТУЗ ) = 4/32 = 1/8; Р( ЧЕРВОВАЯ МАСТЬ ) = 8/32 = 1/4;

Однако имеется одна карта ТУЗ ЧЕРВЕЙ, которая обладает каждым из этих свойств: Вероятность вытащить эту карту равна Р(ТУЗЧЕРВЕЙ )=1/32; Тогда

Пример 1.19. Три стрелка стреляют в мишень. Первый стрелок попадает в мишень с вероятностью 0,9, второй – с вероятностью 0,8, а третий – с вероятностью 0,7. Найти вероятность того, что мишень будет поражена?

Решение: Для решения задачи можно использовать формулу сложения вероятностей. Однако с ростом числа событий эта формула усложняется. С другой стороны, несложно заметить, что событие, попадания в мишень хотя бы одного стрелка, является дополнением события, что мишень после выстрелов останется непораженной (событие ). Событие возможно лишь в случае, когда промахнется каждый из стрелков (промахи и попадания каждого стрелка не зависят от результатов выстрелов других стрелков). Пусть событие А состоит в том, что хотя бы один из стрелков попал в мишень. Поскольку , имеем