Взаимосвязи случайных величин Парная корреляция

Прямое толкование термина "корреляция" — стохастическая, вероятная, возможная связь между двумя (парная) или несколькими (множественная) случайными величинами. При решении различных задач часто возникают ситуации, когда необходимо численно оценить глубину связи между случайными величинами. Для оценки глубины связи для различных типов данных вводятся различные меры. Одной из наиболее часто применяемых мер является коэффициент корреляции, предложенный Пирсоном. Коэффициент корреляции рассчитывается по формуле

и оценивает тесноту линейной связи между случайными величинами и . Можно показать, что коэффициент корреляции принимает значения от -1 до 1. Знак коэффициента характеризует характер поведения в среднем одной случайной величины относительно другой. Если при возрастании (убывании) одной с.в. другая также возрастает (убывает), то коэффициент корреляции имеет положительный знак, если же при возрастании (убывании) одной из них – другая убывает (возрастает), он меньше нуля. Если коэффициент корреляции равен нулю, то X и Y называют некоррелированными. Это не означает, что они независимы, могут существовать какие-то, как правило - нелинейные связи величин, при которых коэффициент корреляции равен нулю.

Обратное всегда верно - если величины независимы, то . Если модуль равен 1, то есть все основания предполагать наличие линейной связи между Y и X.

Схематичное изображение различных вариантов зависимости между и приведено на рисунках ниже

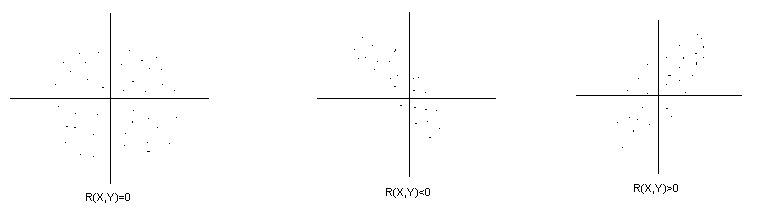
Корреляция по Пирсону определяет степень, с которой значения двух переменных "пропорциональны" друг другу, при этом значение коэффициента корреляции не зависит от масштаба измерения. Например, корреляция между ростом и весом будет одной и той же, независимо от того, проводились измерения в дюймах и фунтах или в сантиметрах и килограммах. Пропорциональность означает просто линейную зависимость. Корреляция высокая, если на графике зависимость "можно представить" прямой линией (с положительным или отрицательным углом наклона).

Элементы математической статистики

Предположим, что поставлена задача оценки качества некоторой продукции, выпускаемой на предприятии. Мы имеем определенное количество экземпляров оцениваемого продукта, имеем возможности для исследования имеющихся экземпляров и должны по результатам исследования дать заключение о качестве продукции предприятия в целом. Рассмотрим характерные особенности решаемой задачи:

1. При проверке качества продукции необходимо ограничиться анализом значений определенных параметров тех экземпляров, которые имеются в наличии. Следовательно, перед решением задачи необходимо определиться с выбором параметров, которые будут оцениваться. В большинстве случаев эти параметры имеют числовой характер.

2. Продукция предприятия имеет неоднородный характер. Следовательно, полученные при анализе значения параметров могут иметь определенный разброс. Наши наблюдения носят ограниченный характер, поскольку анализу подвергается только часть интересующей нас продукции (которая в большинстве случаев целиком и не доступна для анализа), и по результатам конкретной, вообще говоря, небольшой выборки необходимо сделать выводы о всей продукции в целом. При этом важно понимать, как это можно сделать.

3. Поскольку наши знания о небольшой части исследованной продукции мы хотели бы распространить на всю выпускаемую продукцию, любые заключения, сделанные по результатам анализа данных, будут содержать ошибку. Необходимо уметь оценивать величину и вероятность этой ошибки, понимать, как ошибка связана с исследуемой выборкой.

Описанная задача относится к обширному классу задач, решаемых статистическими методами. Например, можно оценивать качество ввозимого товара на таможне, сравнивать показатели работы правоохранительных органов за различные отрезки времени, проводить выборочный анализ оценки знаний студентов, чтобы иметь представление о качестве образования в вузе, оценивать при помощи Exit-пулов предварительные итоги выборов и т.д..

Вообще статистические задачи появляются тогда, когда необходимо дать наилучшие в некотором смысле ответы по ограниченному числу наблюдений.

Математическая статистика в своих решениях опирается на аппарат теории вероятностей, но, тем не менее, используемые модели в теории вероятностей и статистике различны. В самом деле, в теории вероятностей предполагается, что априори известны все сведения об изучаемом объекте, используемый математический аппарат не зависит от предметной области, выводы о поведении исследуемого объекта делаются по всей генеральной совокупности. В задачах математической статистики модель, описывающая исследуемое явление, или неизвестна, или известна только частично. Для определения модели можно проводить пробные испытания. Выводы о поведении объекта делаются по выборке ограниченного объема и распространяются на всю совокупность.

Рассмотрим пример, изложенный в [9], который показывает важность использования математического аппарата при принятии решений.

Пусть имеются два игрока в кости, которые ведут игру по следующим правилам: Производится четыре последовательных бросания кости. Игрок А выигрывает, если по результатам 4 бросаний хотя бы на одной кости выпадает 6 очков, в противном случае выигрыш присуждается игроку В. После каждой игры проигравший выплачивает победителю некоторую денежную компенсацию. В течение какого-то времени, наблюдая игру, наблюдатель должен принять решение кого из игроков ему заменить и с выгодой для себя принять участие в игре. Как правильно осуществить выбор?

Рассмотри три возможных подхода к решению задачи:

Статистический способ принятия решения диктуется обычным здравым смыслом: пронаблюдать какое-то количество (допустим 100) партий, посчитать относительные частоты выигрыша и занять место игрока, который выиграл большее число партий. Если в 52 партиях победу праздновал игрок В, занять его место. При таком решении у наблюдателя должен возникнуть вопрос о надежности принимаемого решения. Ведь продолжение наблюдения за другими сериями бросков могло бы дать совершенно другие результаты, и вполне возможно эти результаты могут наступить после принятия решения с соответствующими последствиями.

Теоретико-вероятностный способ решения: Этот способ основан на определенной математической модели, которая предполагает, что кость абсолютно симметрична и выпадение каждой из граней равновозможны. В рамках этой модели вероятность выпадения грани с номером , равна 1/6. Обозначим через вероятность события, что при бросаниях ни на одной из костей не выпадет значение 6. Поскольку результаты выпадения очков на разных костях независимы, то имеем , откуда с учетом того, что имеем 0,482. Следовательно, в рамках этой модели наблюдатель должен принять сторону игрока А. Слабой стороной такого способа решения является предположение о симметричности кости, поскольку оно относится к некоторому идеальному объекту, а не к конкретной кости, участвующей в игре. Исходы для реальной кости могут в действительности быть и не равновозможными.

Вероятностно-статистический способ принятия решения. Попробуем объединить два предыдущих подхода. Как и в первом случае, мы сначала собираем статистическую информацию, которая характеризует свойства реальной кости. Пусть мы получили, что частота наступления события «не шесть» при партиях равна . Истинное значение вероятности этого события, которое нам неизвестно, обозначим через . Число выражает погрешность приближения вероятности частотой . Поскольку при различных сериях наблюдений значение изменяется, является случайной величиной. Используя результаты теории вероятностей можно показать, что для любого числа , при достаточно больших значениях выполняется

.

Это означает, что с вероятностью можно гарантировать погрешность будет лежать в интервале

,

границы которого определены неизвестным значением . Решая неравенство относительно , получим неравенство

,

которое дает новую оценку

.

При , n=100 и =0,52 с вероятностью 0,95 имеем , поэтому . Следовательно, наблюдения за исходами 100 партий дают нам основания заключить, что с вероятностью 0,95, интересующая нас вероятность исхода лежит в интервале , и, следовательно, может быть как меньше 0,5(тогда необходимо ставить в игре на ситуацию «шесть»), так и больше 0,5 (тогда необходимо ставить в игре на ситуацию «не шесть»)

Другими словами, после наблюдения 100 партий мы не можем принять надежного решения и должны либо продолжить наблюдения до тех пор, пока интервал покрытия интересующей нас вероятности не окажется целиком либо левее, либо правее 0.5, или, заняв место любого из игроков начать играть без особого риска проиграть и без особой возможности выиграть.