17. Многокритериальные задачи в теории принятия решений. Множество решений оптимальных по Парето.

Проблему решения оптимизационных задач с учетом множества показателей эффективности называют проблемой решения многокритериальных задач или проблемой векторной оптимизации.

Отдельном показателем или локальных критерии как правило выражены в разных единицах измерения и свести их в один глобальный критерий задача не достижима. Более того, отдельные критерии противоречивы, добиваясь улучшения одного критерия получим ухудшения другого и наоборот. Даже на уровне системы автоматического регулирования добиваясь сокращения времени переходного процесса приходится мирится с увеличением величины перерегулирования. Формулировка проблемы оптимизации по векторному критерию была в первые сформулирована Вильфредо Парето 1896г. Выбором управления можно оптимизировать какой либо скалярный функционал, однако невозможно в той же допустимой области управлений оптимизировать другой скалярный функционал, даже когда их смысл непротиворечивы.

Таким образом проблема векторной оптимизации – это проблема принятия компромиссного решения.

В настоящие время можно выделить 4 подхода к основной проблеме векторной оптимизации: т.е. к преобразованию множества скалярных функционалов в один глобальный:

1 подход. Построение области Парето и предоставление проектировщику или лицу принимающего решение, возможность выбора единичного из Парето - оптимальных решений.

2 подход. Последовательная оптимизация скалярных критериев после введения для них приоритетов с назначением или без назначения для них уступок.

3 подход. Оптимизация на основе компромиссных отношений, например: путем назначения весовых коэффициентов для каждого скалярного критерия или путем назначения придельных значений для всех критериев, кроме одного главного.

4 подход. Оптимизация основанная на приближении решения к которому. Специальным образом выбранному идеальному значению.

Рассмотрим сущность области Парето

Пусть задача принятия решения состоит в максимизации двух противоречивых и не сводимых друг к другу. Критериев и для системы описываемой дифференциальными уравнениями.

, , , ,

Множество допустимых управлений заданно областью ; а отображение этой области на области функционала ограниченна кривой OCABD. Наибольшее значение критерия достигается в точке В, однако значение критерия в этой точке далеко от максимума. При наибольшем значении критерия в точке А далеко от максимума значение критерия . В точке С оба критерия достигают максимума однако эта точка не принадлежит области допустимых значений и по этому не достижимо. Очевидно что решение необходимо искать на кривой АВ.

Кривая АВ определяет для рассматриваемого примера область Парето которая характеризуется тем свойством, что любое принадлежащий этой области решения нельзя улучшить одновременно по всем скалярным критерием. Действительно выбрав произвольно точку М в допустимой области решения не лежащию на кривой АВ не трудно убедится что определяемая ее решению можно улучшить по критерию в точке и максимум в точке - достигает максимума. Можно улучшить решение одновременно по двум критериям. Это решение лежит на кривой . Из сказанного следует, что:

1. искомое решения должны быть Парето оптимальными, поскольку остальные решения заведомо хуже сразу по всем критериям.

2. Необходима дополнительная информация для единственного решения из множества Парето оптимальных.

Решение (Парето), являются Парето оптимальными для задачи в том и только в том случае если среди всех приращений , не найдется такого, что для всех будет выполнятся условие

2 подход. Проблема векторной оптимизации связанна с упорядочиванием критериев по важности и постарением процедуры последовательной оптимизации сначала по одному критерию затем по второму, по третьему и т.д. Для данной группу характерными являются методы последовательного достижения частных целей и последовательных уступок. На результаты решения существенное влияние оказывает порядок достижения частных целей поэтому все скалярные критерии необходимо с начало упорядочить по приоритетам соотношение вида показывает что критерий , важнее, предпочтительнее критерия .

С начало решается задача максимизация одного критерия , отыскивает оптимальные значения критерия (мах) , затем назначает уступку на критерий и максимизирует критерий при условии, что

- потеря эффективности критерия .

Затем назначают уступку , максимизируют критерий , назначаю при этом уступку на и и т.д.

Недостатком метода последовательных уступок следует отнести необходимость формирования экспертных оценок как для назначения приоритетов, так и для назначения уступок; а также необходимость применения различных процедур оптимизации, если скалярные критерии имеет различную математическую форму.

К 3^ей группе методов относятся метод компромиссных отношений, в которой устанавливают определенные весовые соотношения между локальными критериями, наиболее распространенный способ скаляризации состоит в формировании общего критерия в виде суммы локальных критериев.

-весовые коэффициенты определяющие вклад(вес) соответствующего локального критерия в глобальный(общий) критерий.

Задача определения весовых коэффициентов не менее сложна, чем задача выбора уступок и назначение приоритетов. Эту задачу назначение весовых коэффициентов решают также методом экспертных оценок.

Методы скаляризации 4^ой группы основаны на введение тем или иным способом идеального (утопического) решения и на приближение к этому идеального решению. Наиболее часто, идеальное решения задают в пространстве максимизируемых функционалов утопической точкой.

Эта идеальная точка получается в результате максимизации локальных критериев и соответствует максимальных критериев и соответствует максимальному значению каждого локального критерия.

Нормой приближения к этому идеальному решению обычно принимают меру и ее минимизируют.

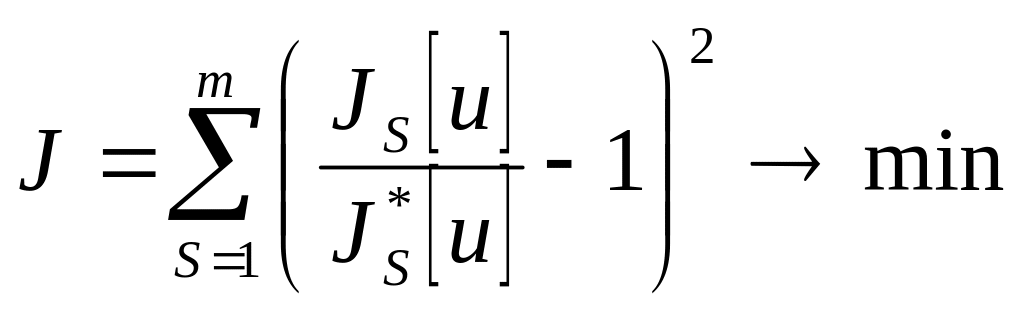В этом случае решение распадается на 2 этапа:

1 этап – определение оптимальных значений каждого критерия независимо от оптимальных, т.е. нахождение идеальной точки.

2 этап – минимизируется отклонения от идеальной точки.