
- •1 Основные этапы принятия решения. Пример количественного анализа принимаемого решения при сбыте продукции.
- •2. Алгоритм управления переходным процессом.
- •3,9 Особености задачи классического вариационного исчления и задач управления реальными процессами. Три задачи оптимального управления. Сведение их к задаче минимизации координаты процесса
- •5.Функция полезности. Отношение к риску.
- •7. Задача с вазами.
- •8 Оптимизация многостадийных процессов. Постановка задачи.
- •10. Основная задача управления. Условие разрешимости принципа при построении оптимальной стратегии управления.
- •11.Принцип оптимальности Беллмана. Применение принципа при построении оптимальной стратегии управления.
- •12. Синтез оптимального регулятора. Решение задачи принципа максимума.
- •13.Метод динамического программирования в непрерывной форме.
- •14. Геометрическая интерпретация озу.
- •1 5. Формулировка принципа максимума в задаче со свободным концом.
- •16. Многокритериальные задачи теории принятия решений. ОзУи метод ее решения.
- •17. Многокритериальные задачи в теории принятия решений. Множество решений оптимальных по Парето.
- •18 Управление динамическими режимами ректификационной установкой. Умб. Условия разрешимости озу.
- •19 Эквивалентные преобразования озу.
- •20.Оптимальное распределение реакционных объемов в каскаде реакторов идеального смешения.
- •2 1. Свойства f-ии Гамильтона.
- •22.Математическая формулировка принципа оптимальности.
- •23. Свойства озу в линейной постановке.
- •24 . Показатели функционирования, модель процесса. Постановка задачи управления переходными режимами ректификационных установок.
- •25. Решение оптимизационной задачи путем сведения ее к последовательности решения озу.
- •26.Оптимальный темпиратурный профиль в реакторе идеального вытеснения. Алгоритм.
- •27.,Вычислительная процедура метода динамического программирования.
- •28.Задача максимального быстродействия.
25. Решение оптимизационной задачи путем сведения ее к последовательности решения озу.
![]()
![]() .
Такая задача оптимизации сводиться к
последовательности решения ОЗУ
.
Такая задача оптимизации сводиться к
последовательности решения ОЗУ
![]() где А1-наибольшее значение
функционал
.
где А1-наибольшее значение
функционал
.![]() -первое
приближение нижнего предельного значения
функционала
.
-первое
приближение нижнего предельного значения
функционала
.
Решение Задачи оптимизации строиться
как последовательность решения ОЗУ.
Т.е задается первое приближение границы
![]() при
к=1. Решается ОЗУ , находиться
,
затем назначается второе приближение
при
к=1. Решается ОЗУ , находиться
,
затем назначается второе приближение
![]() ,
снова решается ОЗУ, и назначается третье
приближение
,
снова решается ОЗУ, и назначается третье
приближение
![]() ,
решается Следующее ОЗУ до тех пор, пока
существует решение ОЗУ, таким образом
при некотором управлении
,
решается Следующее ОЗУ до тех пор, пока
существует решение ОЗУ, таким образом
при некотором управлении
![]()
26.Оптимальный темпиратурный профиль в реакторе идеального вытеснения. Алгоритм.
На основе принципа максимума построить
оптимальный температурный профиль в
реакторе идеального вытеснения из
условия следующей задачи: В реакторе
идеального вытеснения протекает реакция
первого порядка A![]() P
Q.
превращения исходного реагента А в
продукт реакции Р. xa,
xp –
концентрации компонентов А и Р,
соответственно. Т – температура реакции;
Е1 и Е2 – энергии активации
реагентов А и Р. Обозначим xa
= x1 , xp
= x2 .Процесс реакции
в реакторе описывается системой
уравнений: {
P
Q.
превращения исходного реагента А в
продукт реакции Р. xa,
xp –
концентрации компонентов А и Р,
соответственно. Т – температура реакции;
Е1 и Е2 – энергии активации
реагентов А и Р. Обозначим xa
= x1 , xp
= x2 .Процесс реакции
в реакторе описывается системой
уравнений: {![]() ;
;![]() ;
с начальными условиями x1(0)=x10,
x2(0)=x20.
;
с начальными условиями x1(0)=x10,
x2(0)=x20.
Управлением процесса является
распределение температуры реактора
Т(t), которое удовлетворяет
ограничениям T1![]() T
T2. Время реакции
задано t
T
T2. Время реакции
задано t![]() [0,k].
Требуется найти такой закон изменения
температуры реактора T0(t),
при котором концентрация продукта на
выходе реактора максимальна, что
соответствует минимуму функционала I
= - x2(k).
[0,k].
Требуется найти такой закон изменения
температуры реактора T0(t),
при котором концентрация продукта на
выходе реактора максимальна, что
соответствует минимуму функционала I
= - x2(k).
Алгоритм решения задачи
Составляется функция H:
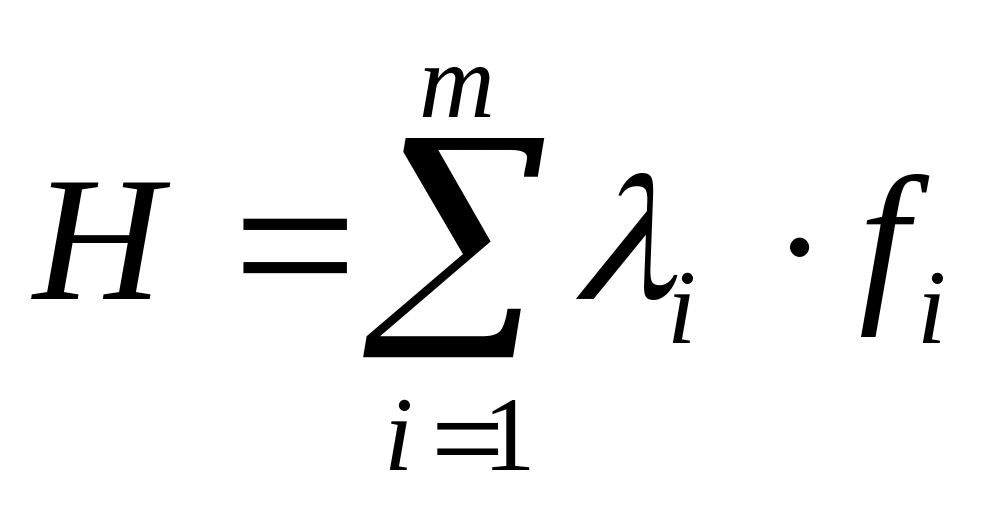 ,
где fi
– правая часть i-ого
дифференциального уравнения, разрешенного
относительно первой производной xi;
i
– сопряженные функции i
= i(t).
Определяется система сопряженных
уравнений:
,
где fi
– правая часть i-ого
дифференциального уравнения, разрешенного
относительно первой производной xi;
i
– сопряженные функции i
= i(t).
Определяется система сопряженных
уравнений:
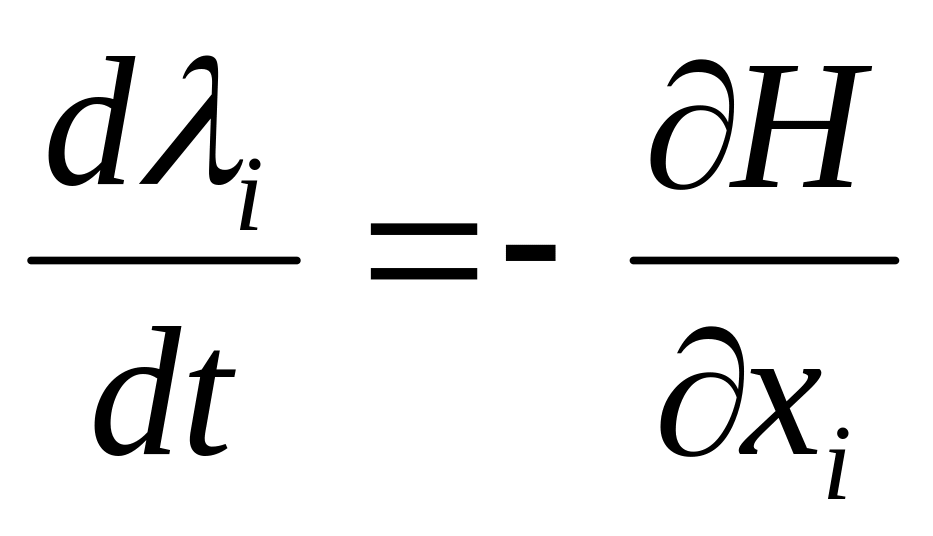 ;
с конечными условиями i(Т)
= - сi, где сi
– коэффициенты функционала.
;
с конечными условиями i(Т)
= - сi, где сi
– коэффициенты функционала.Заданный интервал времени t
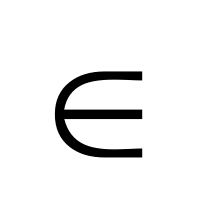 [t0,
T] разбивается на N
– частей с шагом
[t0,
T] разбивается на N
– частей с шагом
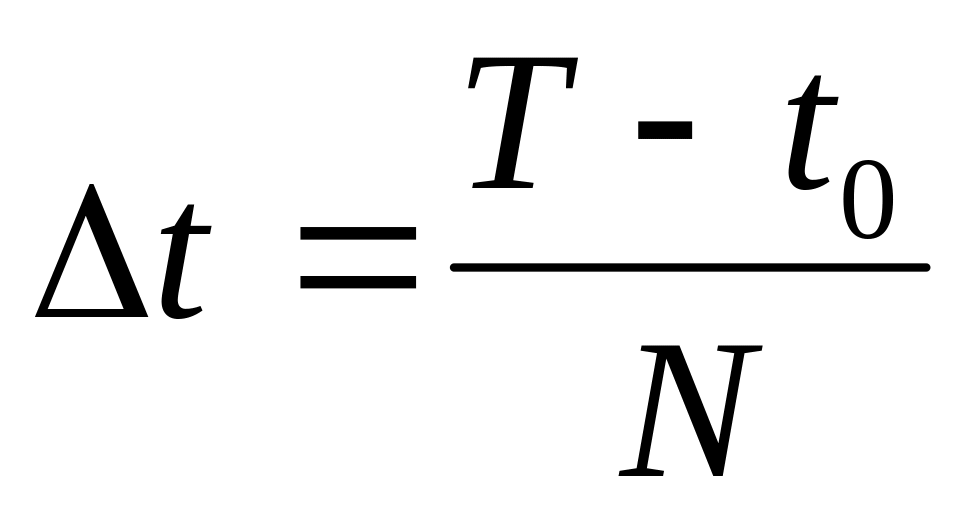 .
.Область изменения управления разбивается на М частей с шагом
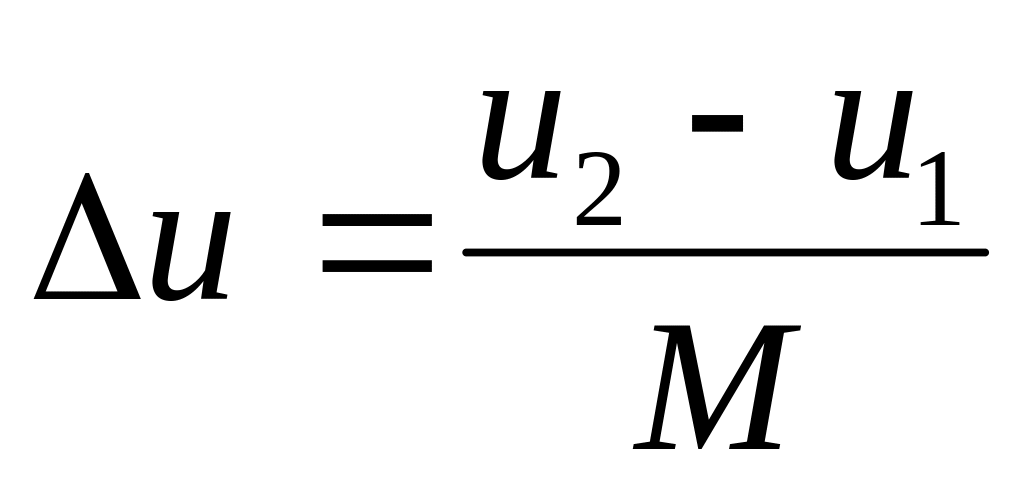 .
.Решение задачи условимся вести от начала интервала t = t0. Поэтому в начале интервала t = t0 произвольно задаются начальные условия для интегрирования сопряженных систем уравнений: i(t0) = i0.
В начале интервала интегрирования t = t0 по известным xi(t0) = xi0, i(t0) = i0, вычисляется значение функции H:
при каждом значении управления u
из области
![]() начиная с u = u1
до u= u2
с шагом u.
начиная с u = u1
до u= u2
с шагом u.
7. Из рассчитанного массива значений функции H выбирается максимальная H и определяется соответствующее этому максимуму оптимальное управление u=uopt(t0).
8. На основе u=uopt(t0) и xi(ti), i(ti) рассчитывается для следующего момента времени t = t + t оптимальная фазовая траектория xiopt(t + t, uopt) и значения сопряженных функций iopt(t + t, uopt).
9. Используя рассчитанные xiopt(t + t) и iopt(t + t) в исходных и сопряженных уравнениях для времени t = t + t вычисляется функция H(t + t) для каждого уравнения u из области (u1,u2) так же, как это описано для t = t0.
Процедура расчета повторяется, начиная с п.6 при каждом новом значении t = t + t до тех пор, пока не будет рассчитано управление на всем интервале времени от t0 до T.
11. В конце интервала интегрирования
необходимо проверить выполнение конечных
условий для функции i(T)
= - ci
. Если расчетное значение i(T)![]() - ci с
определенной степенью точности
- ci с
определенной степенью точности
![]() ,
то начальные значения i(t0)
= i0
заданы неверно. Требуется изменить
начальные значения i(t0)
= i0
так, чтобы конечные i(T)
были равны заданным i(T)
= - ci
с допустимой погрешностью
,
то начальные значения i(t0)
= i0
заданы неверно. Требуется изменить
начальные значения i(t0)
= i0
так, чтобы конечные i(T)
были равны заданным i(T)
= - ci
с допустимой погрешностью
![]() .
При каждом новом значении i0
процедура расчета повторяется, начиная
с п.5. Для определения начальных значений
i0
можно использовать один из методов
нелинейного программирования. Критерием
окончания поиска может служить условие
.
При каждом новом значении i0
процедура расчета повторяется, начиная
с п.5. Для определения начальных значений
i0
можно использовать один из методов
нелинейного программирования. Критерием
окончания поиска может служить условие
![]() .
.
