13.Метод динамического программирования в непрерывной форме.
Рассмотрим непрерывный процесс, описанный системой дифференциальных уравнений
-
вектор управления
Требуется найти такое управление , которое обеспечивает минимум функционалу
(2)
Рисунок
-
2 стадии непрерывного процесса
Обозначим минимум значения функционала на 2 последнем отрезке
x- состояния входа, t – время.
Разобьем этот интервал на 2 интервала
Рис
Где
-
бесконечно малая величена
Запишем уравнение (3) на этих 2-х отрезках
Используя принцип оптимальности:
(4)
Обозначим через
Подставив в (4)
Поскольку значение
от выбора управления не зависит, то ее
можем внести под знак минимума и тогда
выражение (5)
Разделим каждое слагаемое этого уровня
на
Перейдем к приделу при
На основании теоремы о среднем значении
интеграла на бесконечно малом отрезке
времени
Пояснение
Рисунок
Тогда
(5а)
(6)
-
полная производная этой функции.
Вместо
Полученное выражение полной производной составляет в силу уравнения движения (1)
Подставив в уравнение (5а) значение полной производной
-
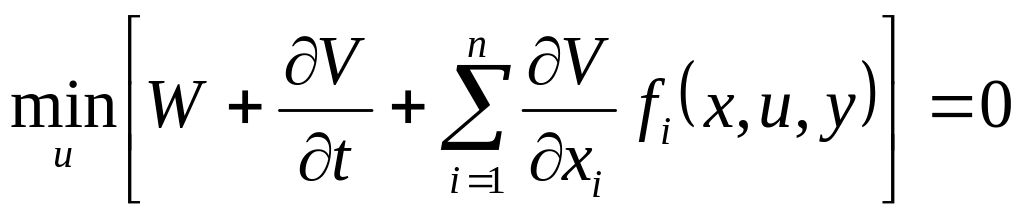
частная производная независим от
управления
,
поэтому ее можно вынести за знак минимума.
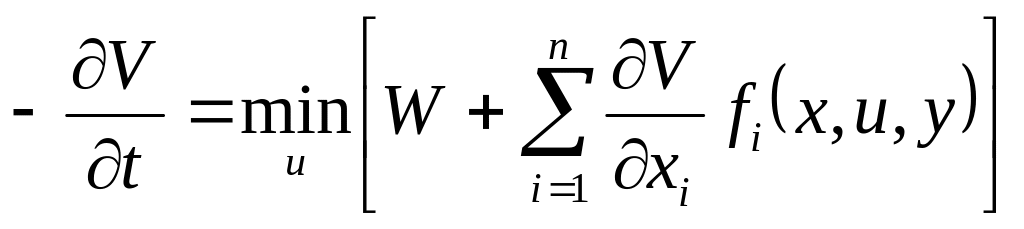(7)
Это уравнение должно для непрерывных процессов.
Из этого уравнения находятся оптимальное уравнение и Функционала при этом для определения оптимизации управления использует необходимое условие экстремума функции.
14. Геометрическая интерпретация озу.
Пусть вектор управления U и вектор функционала J имеет по две компоненты:
U=(U1, U2);
J=(J1, J2)
У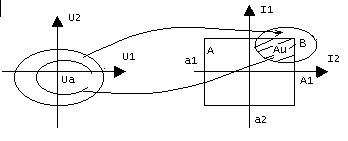
правление
принимает
свои значения из области U,
а функционалы J из
прямоугольника
a1≤J1≤A2; a2≤J2≤A1
Задавая различные управления U1,U2 из области U и используя уравнение процесса, получим на плоскости функционалов некоторую область В. Т.е. область U отображается в область В. Пересечение областей А и В - это есть область выполнения ограничений при допустимых управлениях U. При заданной области допустимых управлений U реализуется область Au= А∩В является пересечением областей А и В. Отображая Au на область допустимых управлений получим область возможных решений ОЗУ Ua.
Геометрическая интерпретация построения решения ОЗУ.(совместно с эквивалентными преобразованиями)
Для иллюстрации идеи метода решения
ОЗУ рассмотрим частный случай, когда
система характерезуется только двумя
односторонними неравенствами.
или
одним двухсторонним
и имеет один скалярный управляющий
параметр
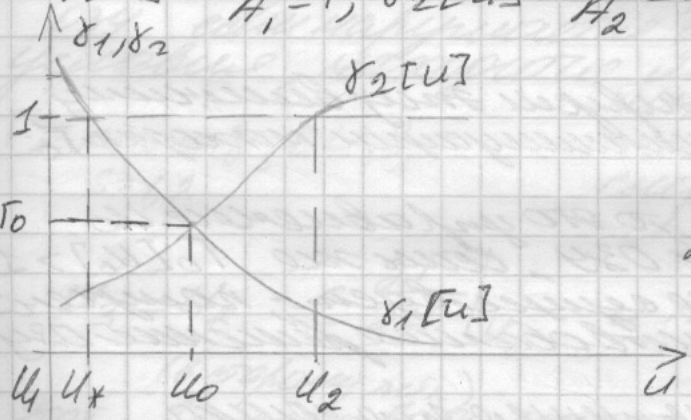
допустимая
область изменения управляющих параметров.
Показатели
не
должны превосходить единицу, управления
u, удовлетворяющее условию
Находиться в области
Характерным здесь является решение
,
при котором
равны
между собою
,
с другой стороны используя неравенство
(1),(3) получим что если
(5),
то
(6)
и наоборот из неравенства (6) следует
неравенство (5) и(1) таким образом
неравенства (1), (5),(6) эквивалентны друг
другу и могут заменять друг друга. В
дальнейшем будем пользоваться вместо
неравенства (1) неравенством (6).
Предварительно введем обозначение
тогда неравенство (6) будет иметь вид
Таким
образом суть этих преобразований в том,
что двухстороннее неравенство(1) привели
к односторонним неравенствам (7),
показатели процесса сделали безразмерными
и пределы изменения функционала сделали
одинаковыми от 0 до 1, и эквивалентная
формулеровка задач ОЗУ для процесса
описываемого системой уравнений
Требуется
найти такое управление
,
которое обеспечит выполнение неравенства
при
выполняется
условие
Есть точка минимакса критериев
,
т.е наибольшее имеет минимум. Для
вычисления
сначала
фиксируем управление
и
находим наибольшее из двух величин
.
Оно равно
если
u лежит в интервале
и
равно
если
u лежит в интервале
Далее минимизируем эту величину т.о. в
результате минимизации находим
Если
,то
это управление
будет решением ОЗУ.Если же
то решение ОЗУ не существует ,полученное
условие существование решение ОЗУ.
используется для поиска решения одним
из методов программирования . Например
метод градиентного спуска. Например
зададим какое-то значение управления
.При
этом управление вычислим критерии
Если
то [
]
-решение ОЗУ.Если же при этом управление какой-нибудь из этих критериев >1.то
не яв-ся решением ОЗУ.Пусть
,тогда
построим следующее приближение управления
,где
-величина
шага спуска .При новом управление
выполняется критерий
и проверяется условие
Если условие верно то
-решение
ОЗУ. Если нарушается одно или оба условия
находиться
из
них при этом управление
и строится следующее приближение
и
т.д этот процесс продолжается до тех
пор пока не получим управление при
котором
S=1,2m
или не найдем минимаксное значение
критерия
Если
то
полученое управление является решением
минимаксной задачи и одним из решения
ОЗУ.