
- •1 Основные этапы принятия решения. Пример количественного анализа принимаемого решения при сбыте продукции.
- •2. Алгоритм управления переходным процессом.
- •3,9 Особености задачи классического вариационного исчления и задач управления реальными процессами. Три задачи оптимального управления. Сведение их к задаче минимизации координаты процесса
- •5.Функция полезности. Отношение к риску.
- •7. Задача с вазами.
- •8 Оптимизация многостадийных процессов. Постановка задачи.
- •10. Основная задача управления. Условие разрешимости принципа при построении оптимальной стратегии управления.
- •11.Принцип оптимальности Беллмана. Применение принципа при построении оптимальной стратегии управления.
- •12. Синтез оптимального регулятора. Решение задачи принципа максимума.
- •13.Метод динамического программирования в непрерывной форме.
- •14. Геометрическая интерпретация озу.
- •1 5. Формулировка принципа максимума в задаче со свободным концом.
- •16. Многокритериальные задачи теории принятия решений. ОзУи метод ее решения.
- •17. Многокритериальные задачи в теории принятия решений. Множество решений оптимальных по Парето.
- •18 Управление динамическими режимами ректификационной установкой. Умб. Условия разрешимости озу.
- •19 Эквивалентные преобразования озу.
- •20.Оптимальное распределение реакционных объемов в каскаде реакторов идеального смешения.
- •2 1. Свойства f-ии Гамильтона.
- •22.Математическая формулировка принципа оптимальности.
- •23. Свойства озу в линейной постановке.
- •24 . Показатели функционирования, модель процесса. Постановка задачи управления переходными режимами ректификационных установок.
- •25. Решение оптимизационной задачи путем сведения ее к последовательности решения озу.
- •26.Оптимальный темпиратурный профиль в реакторе идеального вытеснения. Алгоритм.
- •27.,Вычислительная процедура метода динамического программирования.
- •28.Задача максимального быстродействия.
2. Алгоритм управления переходным процессом.
Для расчета управления u(tk)
в дискретные моменты времени tk
используются уравнения (2) и алгоритм
решения минимаксной задачи. Предварительно
по измеренным значениям параметров
процесса и в предположении, что в
уравнениях (2);
![]() проводится расчет стационарной модели
процесса, вычисляются значения
функционалов Js
(s = 1, 2, ..., 2r)
в момент времени t ==
0, определяются управляющие параметры
статического режима.
проводится расчет стационарной модели
процесса, вычисляются значения
функционалов Js
(s = 1, 2, ..., 2r)
в момент времени t ==
0, определяются управляющие параметры
статического режима.
1. В момент временило t = 0 измеряется величина возмущающего сигнала (0). Вектор возмущающих воздействий в общем случае является функцией времени = ( t). Составляющими вектора , как правило, являются изменения расхода F и состава х F сырья, поступающего в аппарат: (t) = [F (t),хF (t)]
2. Задается длительность первого такта управления = t1 - to и первое приближение управления u(1) (t1). В качестве первого приближения можно принять значение управления, соответствующее статическому режиму.
3. На основании первого приближения управления u(1) (t1) и вектора возмущающих воздействий
(0) решаются уравнения (2), определяются
значения фазовых координат
![]() в первом приближении и вычисляются
величины функционалов Js
[u(1) (t1)]
(s =1, 2, …, 2r).
в первом приближении и вычисляются
величины функционалов Js
[u(1) (t1)]
(s =1, 2, …, 2r).
4. Среди функционалов Js, (s = 1, 2, ..., 2r) выбирается наибольший по значению функционал, например J = max Js,.
5. Если J 1, то остальные (2г-1) функционалов будут также Js 1 (s = l,2,...,2r - l).
В этом случае при t
= t1
выполняются ограничения на значения
функционалов (7) и управление u(1)(t1)
- одно из решений задачи. Если же J
> 1, то значение функционала J
минимизируется выбором следующего
приближения управления:
![]()
6. С использованием второго приближения
управления u(1)(t1)
в ypaвнениях (2) определяются
значения фазовых координат
![]() во втором приближении, рассчитываются
функционалы Js[u(2)
(t1)]. Снова выбирается
наибольший но значению функционал и,
если его значение больше единицы,
рассчитывается повое приближение
управления. Если же значения всех
функционалов удовлетворяют неравенствам
Js
1 (s = 1, 2, ..., 2r), то одно из решений
задачи u(р)(t1)
и дискретной точке t1
найдено. Управление u(р)(t1)
может быть рассчитано заранее до
наступления момента времени t1.
во втором приближении, рассчитываются
функционалы Js[u(2)
(t1)]. Снова выбирается
наибольший но значению функционал и,
если его значение больше единицы,
рассчитывается повое приближение
управления. Если же значения всех
функционалов удовлетворяют неравенствам
Js
1 (s = 1, 2, ..., 2r), то одно из решений
задачи u(р)(t1)
и дискретной точке t1
найдено. Управление u(р)(t1)
может быть рассчитано заранее до
наступления момента времени t1.
7. В момент времени t1 управление u(р)(t1) подается на исполнительные механизмы, установленные па линии управляющих потоков. На этом первый такт управления заканчивается.
8. Второй такт управления начинается с
измерения возмущений (t1)
в дискретной точке u(р)(t1).
Задается время такта
![]() и рассчитывается управление в дискретной
точке t2 по
алгоритму, начиная с п. 2. 9. Аналогично
осуществляется следующий такт управления.
На каждом такте управления проводится
измерение возмущений, расчет и выдача
управляющих воздействий на исполнительные
механизмы аппарата.Число тактов
управления определяется временем выхода
колонны в установившийся режим.
и рассчитывается управление в дискретной
точке t2 по
алгоритму, начиная с п. 2. 9. Аналогично
осуществляется следующий такт управления.
На каждом такте управления проводится
измерение возмущений, расчет и выдача
управляющих воздействий на исполнительные
механизмы аппарата.Число тактов
управления определяется временем выхода
колонны в установившийся режим.
3,9 Особености задачи классического вариационного исчления и задач управления реальными процессами. Три задачи оптимального управления. Сведение их к задаче минимизации координаты процесса
Управление реальными механическими объектами представляет собой обычно кусочно непрерывные функции с конечным числом точек разрыва 1го рода
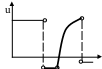
![]()
![]()
![]()
Фазовые координаты процесса
![]() как
решение системы описывающей состояние
объекта является также ограниченными
величинами и тоже могут иметь
кусочно-непрерывный характер.
Действительно, в качестве управления
обычно выступают некоторые технологические
параметры: расход веществ, температура
давление и т.д., которые не могут принимать
сколь угодно больших или малых значений,
и фазовые координаты
как
решение системы описывающей состояние
объекта является также ограниченными
величинами и тоже могут иметь
кусочно-непрерывный характер.
Действительно, в качестве управления
обычно выступают некоторые технологические
параметры: расход веществ, температура
давление и т.д., которые не могут принимать
сколь угодно больших или малых значений,
и фазовые координаты
![]() ,
которые могут быть концентраций,
температурой уровень и т.д. тоже являются
ограниченными. Для решения таких задач
использования классического вариационного
исчисления возможно только в частных
случаях, поскольку под интегральная
функция функционала должна быть
непрерывной и как минимум дважды
непрерывно дифференцируемой по
совокупности своих аргументов.
,
которые могут быть концентраций,
температурой уровень и т.д. тоже являются
ограниченными. Для решения таких задач
использования классического вариационного
исчисления возможно только в частных
случаях, поскольку под интегральная
функция функционала должна быть
непрерывной и как минимум дважды
непрерывно дифференцируемой по
совокупности своих аргументов.
![]()
Для решения задачи управления реальными объектами в 1956г. Советскими учеными во главе с академиком Л.С, Понтрягиным разработан метод, который называется принцип максимума.
Все задачи оптимального управления можно свести к 3 типам задачам:
Задача максимального быстродействия. В этой задаче необходимо перевести систему из некого начального состояния в конечное за минимальное время
Задача управления конечным состоянием. В этой задачи необходимо найти управления, которое приводит систему в заданную конечную точку с минимальным отклонением от нее.
Задачи по минимуму интервала.
![]()
Найти управление для процесса описываемого
уравнениями, которое минимизирует
интеграл
![]() .
.
Надо сказать, что все три задачи можно свести к одной к задачи, минимизации одной координаты процесса.
Покажем на примере, что задача по минимуму
интеграла может быть сведена к задачи
минимизации дополнительной координатой
процесса. Дополним систему уравнений
(1) уравнениями вида
![]()
![]()
В общем случае функционал можно записать некую функцию от фаз x координат процесса, в конечный момент времени.
