7.1. Процедуры решения ду в среде mathcad. Примеры соответствующих документов mathcad.

m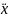 +kx=0 <=> = ((-k)/m)*x <=> с-ма подготовленная к решению

y₀=x(t) y₁=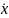 (t) t-независимая переменная x(t) – неизвестная ф-я

M: = 1 k:=5 tbegin:=0 tend:=10

h:=0,2 шаг по времени N:=(tend-tbegin)/h - количество шагов

D(t, y):=(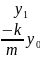 ) – определили ф-ю с именем (дельта (написать значек ;) ) от 2-х параметров,описывающих с-му ур-ий.

y-вектор t- должен стоять переметр описыв. Независим вектор.

y₀- первая компонента вектора y; y₁- вторая компонента вектора y;

yBEGIN:=(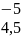 ) – вектор начальных условий; -5 -> x в момент времени t₀; 4,5 -> x в момент времени t₁

S:Rkadapt(YBEGIN,tBEGIN,tEND,N,D)

Rkadapt – имя встроенной процедуры для решения с-мы ур-ий методом Ронгекута с адаптацией шага.

Для вывода значений S пишем «S=» правее или ниже S:=Rkadapt(…..)

Для того чтобы отобразить реш в виде графиков:

Изменения перемещ. к скорости в завти от времени;; rfixed – метод Ронгекута с фиксированным шагом

8.1. Последовательность получения математической модели колебательной механической системы с сосредоточенными параметрами.

q1,q2 обобщенные перемещения. Считаем что они отсчитываются от неподвиж. Поверхности, соответствующей статическому равновесию системы.

Выражаем удлинения пружин и скор удлинения демпферов

Составляем выражения для кинетической энергии системы

Составляем выражение для потенциальной энергии системы

Составляем выр-ие для диссипативной функции

Вычисляем частные производные уравнений лагранжа dT/dq, dT/dq' dП/dq dФ/dq'

Подставляем их в ур-ие лагранжа dT/dq'=Q(t)- dП/dq- dФ/dq'

Устанавливаем начальные условия.

9.1. Численные методы решения оду.

Шаговые методы решений

Интервал интегрирования разбивают на подинтервалы с каким-то шагом. Шаг может менятся или быть постоянным. Если разработать способ получения решения в конце заданного шага, по известному значению решения в нач шага, то можно использовать его в цикле по шагам. Поэтому вся задача сводится к получению решения для шага. Но при этом будет существовать локальная погрешность она будет зависеть от метода построения приближ-го решения и от величины шага. у(с волной)+О(hⁿ⁺¹)=y(x₁). О- величина того-же порядка что hⁿ⁺¹ величина n зависит от метода построения решения и называется порядком метода. Существуют след методы метод эйлера(усовершенствованный МЭ,метод рунге-кутта, метод одной шестой)

10.1. Метод Эйлера и его модификации для решения оду

Если заменить площадь криволинейной трапеции, представляющей собой величину этого интергала, например, на площадь прямоугольника

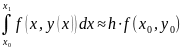
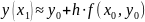
y=y(x)

Y

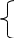
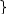
y₀

X

- Ф-ла Эйлера реализующая метод Эйлера. Можно показать, что локальная погрешность этой ф-лы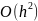 , т.е. метод Эйлера является методом 1-го порядка точности.

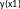
X₀

X₁

α₀

h

Δy

Модификации метода Эйлера

h

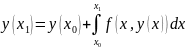
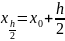
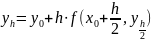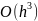Можно показать, что погрешность этой ф-лы – – метод 2-го порядка. Точность увеличивается на порядок, но приходится ещё раз обращаться к правой части ДУ