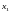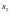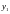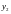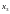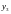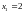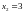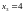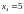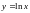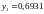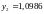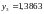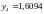21.2. Остаточный член интерполяционной формулы Лагранжа.

Интерполяционная формула Лагранжа это один из наиболее распространенных способов построения интерполяционного полинома. Пусть имеем функцию:

зависит от расположения узлов на интервале интерполирования. Для сравнения приведем значения и соответствующей таблицы: ln(2,5)=0,9163.

Пусть f(x) – интерполируемая функция. Заменим эту функцию полиномом Лагранжа: f(x)=L_n-1+R(f,x). R(f,x) – остаточный член формулы Лагранжа, который представляет собой погрешность метода интерполяции. При выполнения вычисления, результаты отдельных арифметических операций округляются или отсекаются из разряда, поэтому при построении интерполяционного полинома кроме погрешности метода будет присутствовать еще вычислительная погрешность. Можно доказать следующие утверждение: если функция f(x) n раз непрерывно дифференцируема на отрезке [a,b], содержащем узлы интерполирования x₁, x₂, …., x_n, то такая что , где w_n(x)= . Пусть M_n= , . Понятно, чтобы использовать эту теорему нужно иметь возможность взять производную . Интерполяционный полином можно построить единственным образом по данным таблицы. Остаточный член R(f,x) всегда имеет один и тот же вид.

22.2. Интерполяционная ф-ла Лагранжа – один из наиболее распространенных способов построения интерполяционного полинома.

Введем предварительно в рассмотрение так называемые полиномы влияния .

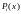Этот полином должен удовлетворять следующим условиям:

1. степень полинома должна быть равна (n-1);

2. 

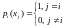
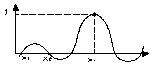
Очевидно, что полином степени (n-1) , равный нулю во всех узлах кроме i- того, имеет вид:

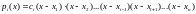
Остается определить константы С из условия

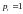
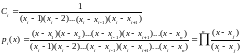
Полином Лагранжа обычно обозначают .

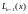Очевидно, что

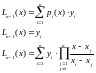
Рассмотрим два частных случая полинома Лагранжа:

1. Пусть имеется таблица из двух точек

Тогда интерполирующий полином будет выглядеть

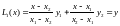
Это так называемый случай линейной интерполяции, поскольку данное уравнение - это уравнение прямой.

2. Пусть имеется таблица из n=3 точек

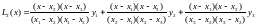
Такое приближение называется параболическим или квадратическим (так как данное уравнение- уравнение параболы).

Рассмотрим пример.

Пусть задана таблица

23.2. Алгебраическое интерполирование.

Алгебраическое интерполирование – это вид приближения, если приближенную функцию обозначить 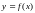, то для таблицы из n точек , необходимо потребовать выполнения условия:

Понятно, что в такой общей постановке решением задачи может оказаться бесконечное решение функций, поэтому, чтобы сделать задачу определенной, необходимо сузить класс подбираемых функций. Как было рассмотрено выше, при наличии определенной информации следует подбирать приближенную функцию так, чтобы она согласовывалась с приближаемыми данными.

Если же такой информации нет, то одним из способов выбора является выбор полинома в качестве приближаемой функции. В этом случае интерполяцию называют алгебраической.

Будем искать интерполянт в виде полинома степени не выше(n-1).

(1)

Тогда условие (1) примет вид:

(2)

Понятно, что вид интерполирующего полинома полностью определяется набором коэффициента.

Рассмотрим следующее утверждение:

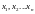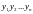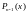Пусть в n попарно-различных точках заданы числа , тогда существует единственный полином степени не выше (n-1), удовлетворяющий условию (*).

Доказательство:

Запишем это условие в каждой точке

Здесь 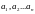- неизвестные, а правые части известны:

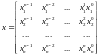(4)

Эта матрица специального вида - матрица Вандерманда. Для нее легко показать, что определитель этой матрицы 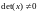отличен от нуля, но если это так, то система (4) имеет единственное решение.

Следствием этого утверждения является то, что вид интерполирующего полинома не зависит от способа его построения. А сам ход рассмотренных рассуждений дает один из способов построения такого полинома.

Рассмотренный способ называется классическим, т.к. в силу единственности интерполяционного полинома, каким бы способом его не строили, результат будет один и тот же.