
- •Понятие о моделировании.
- •2.1. Виды моделирования.
- •3.1. Математическое моделирование. Источники ошибок. Необходимость тестирования.
- •4.1. Сравнительные характеристики пакетов mathcad, matlab, maple, mathematica. Основные приемы работы в mathcad.
- •5.1. Понятие о системах с сосредоточенными и распределенными параметрами.
- •6.1. Сведение системы оду произвольного порядка к системе оду первого порядка в нормализованной форме Коши.
- •7.1. Процедуры решения ду в среде mathcad. Примеры соответствующих документов mathcad.
- •8.1. Последовательность получения математической модели колебательной механической системы с сосредоточенными параметрами.
- •9.1. Численные методы решения оду.
- •10.1. Метод Эйлера и его модификации для решения оду
- •11.1.Методы типа Рунге-Кутта для решения оду
- •13.1. Понятие о граничных задачах для оду. Метод стрельбы для решения граничной задачи.
- •14.1. Построение уравнения изогнутой оси балки при различных условиях на ее концах на основе метода стрельб.
- •15.1.Оценка погрешности решения оду. Способ Рунге для оценки такой погрешности.
- •16.1.Понятие о жестких дифференциальных уравнениях. Процедуры для решения таких уравнений в среде mathcad.
- •17.1. Классификация методов решения оду.
- •19.1. Задача Бюффона как пример использования случайных величин при решении детерминированной задачи.
- •20.1.Вычисление площадей и объемов с использованием случайных величин.
- •21.1.О выборе количества экспериментов для получения заданной степени точности при использовании случайных величин.
- •22.1Метод Судзуо-Какутани для решения граничных задач теории потенциалов
- •23.1. Понятие о конкурирующих стратегиях
- •24.1. Моделирование смо.
- •25.1. Приближение инженерных данных.Виды приближения.
- •Поточечное среднеквадратическое приближение.
- •Непрерывное приближение в среднеквадратичном смысле.
- •Равномерное приближение.
- •1.2.Узловой метод получения математической модели системы.
- •2.2. Метод получения топологических уравнений с использованием м-матрицы.
- •3.2. Получение эквивалентной системы технических объектов.
- •4.2. Компонентные уравнения для различного типа подсистем.
- •Механическая поступательная система.
- •Механическая вращательная подсистема
- •5.2. Основные положения получения математической модели технического объекта на макроуровне.
- •6.2. Особенности выбора узлов сетки при интерполяции различными сплайнами.
- •7.2. Параметрический рациональный сплайн.
- •8.2. Обобщенные кубические сплайны.
- •9.2. Параметрический Эрмитов кубический сплайн.
- •10.2. Интерполяция кривых локальными сплайнами.
- •11.2. Вычисление интеграла по таблице значений функции с использованием интерполирующего полинома Эрмита.
- •12.2. Кубический сплайн дефекта 2 (s3,2(X)).
- •13.2. Определение сплайна. Сплайн первой степени.
- •14.2. Алгоритм «прогонка» для решения системы линейных уравнений с диагональным преобладанием.
- •15. 2. Сплайны. История возникновения. Понятие о звене сплайна.
- •16.2. Использование обратного интерполирования для решения уравнений.
- •17.2. Метод Мюллера для решения трансцендентных уравнений.
- •18.2 Области использования интерполирования.
- •19.2. Тригонометрическая интерполяция.
- •20.2. О наилучшем выборе узлов интерполирования.
- •21.2. Остаточный член интерполяционной формулы Лагранжа.
- •24.2. Разложение аппроксиматора по системе базисных функций.
10.2. Интерполяция кривых локальными сплайнами.

Пусть
имеем кривую, известны толькокоординаты
точек
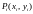 .
В этом случае уже не выполняется условие
упорядоченности абсцисс, которое было
обязательным при построении приближающих
полиномов или сплайнов для обычной
функции. Однако и в этом случае можно
развить аппарат интерполяции сплайнами
плоских или пространственных кривых.
.
В этом случае уже не выполняется условие
упорядоченности абсцисс, которое было
обязательным при построении приближающих
полиномов или сплайнов для обычной
функции. Однако и в этом случае можно
развить аппарат интерполяции сплайнами
плоских или пространственных кривых.
Поступим следующим образом, введем естественную параметризацию кривой.
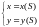
S
– в данном случае это длина дуги,
отсчитываемая от точки
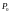 .
Тогда углу
.
Тогда углу
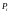 будет соответствовать единственное
значение
будет соответствовать единственное
значение
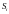 .
.
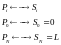
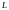 -
общая длина кривой.
-
общая длина кривой.
Рассмотрим интерполяционный сплайн первой степени.
 (1)
(1)
где
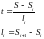
Геометрически такой сплайн представляет собой ломаную, состоящую из кривых, соединяющих между собой точки:
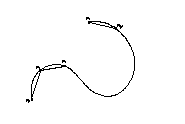
Из условия (1) можно получить
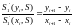 (2)
(2)
где
 ,
а производная взята по параметру t.
,
а производная взята по параметру t.
Как видно, это отношение представляет собой тангенс угла наклона звена сплайна:
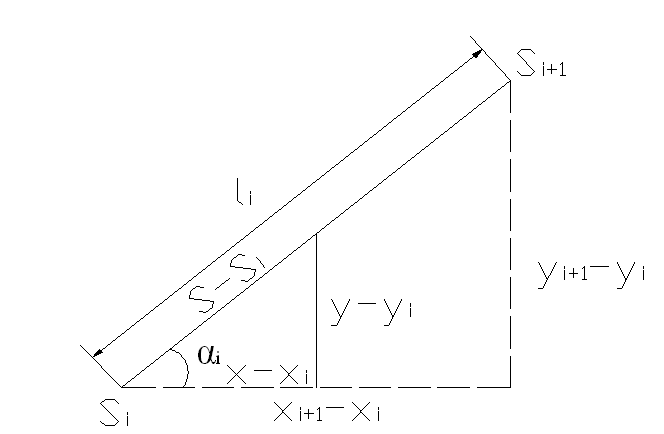
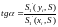
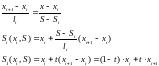
В
этом случае, если звено сплайна
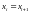 параллельно оси y.
параллельно оси y.
t - безразмерный параметр, который изменяется от 0 до 1.
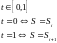
Отметим интересное свойство сплайна, которое заключается в том, что тангенс угла наклона не зависит от S. Положение точки определяется параметром t , изменяя значение которого от 0 до 1 можно получать промежуточные значения на звене сплайна.
Как видно на этом примере (формула 1) параметрический сплайн первой степени в случае плоской кривой представляет собой пару обычных сплайнов. Один для координаты x,а второй для координаты у. В качестве независимой переменной выступает S. Если кривая пространственная, то добавится такая же формула для координаты z.
11.2. Вычисление интеграла по таблице значений функции с использованием интерполирующего полинома Эрмита.
 S3,2(x)=yi∙
F1(t)+
yi+1∙
F2(t)+
mi∙
hi∙F3(t)+
mi+1∙
hi∙F4(t)
S3,2(x)=yi∙
F1(t)+
yi+1∙
F2(t)+
mi∙
hi∙F3(t)+
mi+1∙
hi∙F4(t)
a=x1 x2 xn-1 xn=b
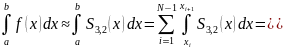
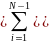
t = , dx=hi∙dt
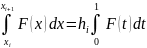
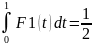
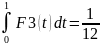
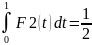
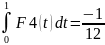
 )
)
12.2. Кубический сплайн дефекта 2 (s3,2(X)).
На участке (xi, xi+1) S3,2(x)=ai0+ai1x+ai2 x2+ai3 x3 (1).
a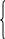 i0,
ai1,
ai2
,ai3
должны
быть определены из условия:
i0,
ai1,
ai2
,ai3
должны
быть определены из условия:
S3,2(xi)=yi (2) – условие непрерывности сплайна
S3,2(xi+1)=yi+1
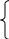 S‘3,2(xi)=mi
(3)
– условие непрерывности производной
S‘3,2(xi)=mi
(3)
– условие непрерывности производной
S‘3,2(xi+1)=mi+1
mi – наклоны сплайна в узлах.
Условия (2) и (3) образуют систему линейных алгебраических уравнений, решив которые можно найти ai0, ai1, ai2 ,ai3 .
Если теперь подставить эти решения в (1), то вид сплайна получится следующим:
S3,2(x)=yi∙ F1(t)+ yi+1∙ F2(t)+ mi∙ hi∙F3(t)+ mi+1∙ hi∙F4(t) (4)
hi= xi+1 – xi
F1(t), F2(t), F3(t), F4(t) – полиномы Эрмита.
F1(t)=(1– t)2(1+2t)
F2(t)=t2(3– 2t) t= , t – безразмерная переменная.
F3(t)=t(1– t)2
F4(t)= – t2(1– t)
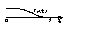
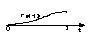
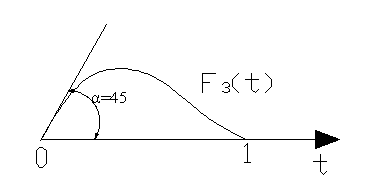
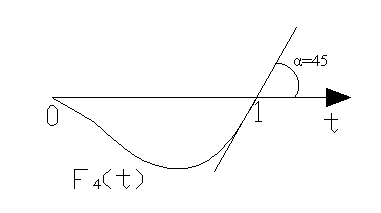
Алгоритм построения данного сплайна.
Проверить на какой из отрезков (xi, xi+1) попадает значение аргумента х, для которого нужно найти S3,2(x). Если при этом окажется, что х= xi , то
S3,2(x)=yi , иначе нужно вычислить hi, затем t, F1(t), F2(t), F3(t), F4(t) и воспользоваться формулой (4).
Если нужно построить значение S3,2(x )с шагом ∆ на интервале (a,b), то к этой функции нужно обратиться в цикле по шагам.
Во многих практических случаях величина наклонов mi неизвестна. Для их определения по заданной таблице (xi,yi) их можно вычислить по приближенным формулам:
mi
 Li∙
Li∙ + Mi∙
+ Mi∙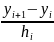 ; i=2,3,…,N-1
(9), т.е. для внутренних участков.
; i=2,3,…,N-1
(9), т.е. для внутренних участков.
m1
(1+M2)∙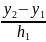 – M2
– M2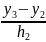 (10),
для левого угла.
(10),
для левого угла.
mn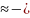 LN-1
LN-1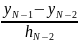 +(1+LN-1)∙
+(1+LN-1)∙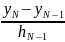 (11)
(11)
Mi
=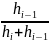
Li=1-Mi
Этот сплайн также относится к семейству локальных сплайнов.
