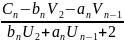- •Понятие о моделировании.
- •2.1. Виды моделирования.
- •3.1. Математическое моделирование. Источники ошибок. Необходимость тестирования.
- •4.1. Сравнительные характеристики пакетов mathcad, matlab, maple, mathematica. Основные приемы работы в mathcad.
- •5.1. Понятие о системах с сосредоточенными и распределенными параметрами.
- •6.1. Сведение системы оду произвольного порядка к системе оду первого порядка в нормализованной форме Коши.
- •7.1. Процедуры решения ду в среде mathcad. Примеры соответствующих документов mathcad.
- •8.1. Последовательность получения математической модели колебательной механической системы с сосредоточенными параметрами.
- •9.1. Численные методы решения оду.
- •10.1. Метод Эйлера и его модификации для решения оду
- •11.1.Методы типа Рунге-Кутта для решения оду
- •13.1. Понятие о граничных задачах для оду. Метод стрельбы для решения граничной задачи.
- •14.1. Построение уравнения изогнутой оси балки при различных условиях на ее концах на основе метода стрельб.
- •15.1.Оценка погрешности решения оду. Способ Рунге для оценки такой погрешности.
- •16.1.Понятие о жестких дифференциальных уравнениях. Процедуры для решения таких уравнений в среде mathcad.
- •17.1. Классификация методов решения оду.
- •19.1. Задача Бюффона как пример использования случайных величин при решении детерминированной задачи.
- •20.1.Вычисление площадей и объемов с использованием случайных величин.
- •21.1.О выборе количества экспериментов для получения заданной степени точности при использовании случайных величин.
- •22.1Метод Судзуо-Какутани для решения граничных задач теории потенциалов
- •23.1. Понятие о конкурирующих стратегиях
- •24.1. Моделирование смо.
- •25.1. Приближение инженерных данных.Виды приближения.
- •Поточечное среднеквадратическое приближение.
- •Непрерывное приближение в среднеквадратичном смысле.
- •Равномерное приближение.
- •1.2.Узловой метод получения математической модели системы.
- •2.2. Метод получения топологических уравнений с использованием м-матрицы.
- •3.2. Получение эквивалентной системы технических объектов.
- •4.2. Компонентные уравнения для различного типа подсистем.
- •Механическая поступательная система.
- •Механическая вращательная подсистема
- •5.2. Основные положения получения математической модели технического объекта на макроуровне.
- •6.2. Особенности выбора узлов сетки при интерполяции различными сплайнами.
- •7.2. Параметрический рациональный сплайн.
- •8.2. Обобщенные кубические сплайны.
- •9.2. Параметрический Эрмитов кубический сплайн.
- •10.2. Интерполяция кривых локальными сплайнами.
- •11.2. Вычисление интеграла по таблице значений функции с использованием интерполирующего полинома Эрмита.
- •12.2. Кубический сплайн дефекта 2 (s3,2(X)).
- •13.2. Определение сплайна. Сплайн первой степени.
- •14.2. Алгоритм «прогонка» для решения системы линейных уравнений с диагональным преобладанием.
- •15. 2. Сплайны. История возникновения. Понятие о звене сплайна.
- •16.2. Использование обратного интерполирования для решения уравнений.
- •17.2. Метод Мюллера для решения трансцендентных уравнений.
- •18.2 Области использования интерполирования.
- •19.2. Тригонометрическая интерполяция.
- •20.2. О наилучшем выборе узлов интерполирования.
- •21.2. Остаточный член интерполяционной формулы Лагранжа.
- •24.2. Разложение аппроксиматора по системе базисных функций.
13.2. Определение сплайна. Сплайн первой степени.
Функция Sn,ν (x) – сплайн степени n дефекта ν, где n и ν - целые числа, если
на каждом из отрезков (xi, xi+1) из (a,b) функция Sn,ν (x) является полиномом степени n;
если Sn,ν (x) на всем интервале (a,b) имеет непрерывные производные до порядка
n- ν включительно.
Кусочные полиномы, образующие сплайн, называются звеньями, а условия непрерывности в узлах____
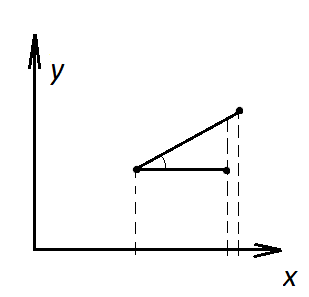
Рассмотрим сплайн 1-ой степени S1(x). Он представляет собой непрерывную кусочно-линейную функцию. На каждом из отрезков (xi, xi+1) он является полиномом 1-ой степени:
S1 (x) = A0+A1∙x
ν=1, т.е. непрерывной производной он не имеет.
Уравнение сплайна:
S1(x)
=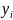 +
(
+
(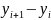 ),
xi
),
xi i+1
i+1
hi =xi+1 – xi - шаг
Для построения этого сплайна требуется только таблица (xi ,yi). Вычисление этого сплайна можно выполнять по следующему алгоритму:
определение tg угла наклона:
tgαi
=
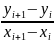 =
=
и вычисляется S1 (x)= +Ui ∙ (x – xi ).
 (xi+1,yi+1)
(xi+1,yi+1)
 Ui(x-xi)
Ui(x-xi)
 (xi,yi) α
(xi,yi) α
S1(x)
yi
xi x xi+1
Сплайн 1-ой степени относится к семейству локальных сплайнов, т.к. для его построения необходима информация только об ограничивающих данный участок узлах.
14.2. Алгоритм «прогонка» для решения системы линейных уравнений с диагональным преобладанием.
Рассмотрим для определенности систему линейных уравнений для непериодического сплайна:
2 M1+M2=C1
M1+M2=C1
aM1+2M2 +b2M3=C2
...
an-1 ∙Mn-2+2Mn-1+bn-1 ∙Mn=Cn-1
Mn-1+2Mn=Cn
Разрешим 1-ое уравнение относительно M1:
M1=p1∙M2+q1
p1=
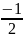 q1=
q1=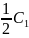
Подставим M1 во 2-ое уравнение и выразим M2:
M2=
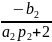 ∙
M3+
∙
M3+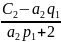
p2=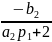 q2=
q2=
M2= p2∙ M3+q2
Продолжая процесс исключения и подставляя Mi-1= pi-1∙ Mi+qi-1 в уравнение
ai ∙Mi-1+2Mi+bi ∙Mi+1=Ci получим:
Mi
=
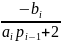 ∙
Mi+1
+
∙
Mi+1
+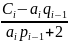 ,
т.е.
pi
и
qi
равны:
,
т.е.
pi
и
qi
равны:
p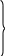 i=
-рекуррентные
формулы для p
и
q.
(1)
i=
-рекуррентные
формулы для p
и
q.
(1)
qi=
Продолжая этот процесс, получим для последнего уравнения:
Mn-1= pn-1∙ Mn+qn-1
Mn-1= -2Mn+Cn
Можно последовательно вычислить:
Mn=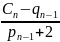 (2)
(2)
M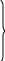 n-1=
pn-1∙
Mn+qn-1
n-1=
pn-1∙
Mn+qn-1
Mn-2= pn-2∙ Mn-1+qn-2 (3)
и т. д.
Т.о. алгоритм «прогонка» состоит из двух частей: прямой и обратный ход.
В прямом ходе сначала задаем p1 и q1, затем по рекуррентным формулам вычисляем прогоночные коэффициенты.
Обратный ход: сначала по формуле (2) вычисляем Mn , а затем по формулам (3) вычисляют Mn-1, Mn-2, …, M1.
Оказывается, метод «прогонка» не приводит к накоплению ошибок округления при вычислении. Такие методы называются численно устойчивыми.
Сформируем систему для случая периодического сплайна:
Из формул
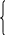 M1=Mn
M1=Mn
ai ∙Mi-1+2Mi+bi ∙Mi+1=Ci , i=2,3,…,h-1.
Mn+1= M2 (hn=h1)
при i=2, M1=Mn получим:
2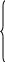 M2+b2M3+
a2
Mn=C2
M2+b2M3+
a2
Mn=C2
a3 M2+2M3+ b3 Mn=C3
… (4)
an-1 Mn-2+2Mn-1+ bn-1 Mn=Cn-1
bn ∙Mn-2+an Mn-1+ 2 Mn=Cn
Эти уравнения аналогичны рассмотренному выше приему и их можно переписать:
Mi= pi∙Mi+1 +ri∙Mn+qi , i=2,3,…,n-1 (5)
Прогоночные коэффициенты опять вычисляются по (1) при условии, что pi= qi=0:
ri
=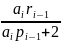 ,r1=1
(6)
,r1=1
(6)
П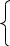 олагая
Mi=Ui∙Mn+Vi
, i=2,3,…,n-1.
олагая
Mi=Ui∙Mn+Vi
, i=2,3,…,n-1.
Ui=pi∙Ui+1+ri
Vi=pi∙Vi+1+qi
Un=1 Vn=0
Mn=