19.Двумерная плотность вероятности и ее свойства.

Случайный вектор называется непрерывным, если существует такая непрерывная неотрицательная функция p(x,y), что для любых x,y R выполняется соотношение

При этом p(x,y) – двухмерная плотность вероятности.

Свойства.

1. p(x,y)=

2. P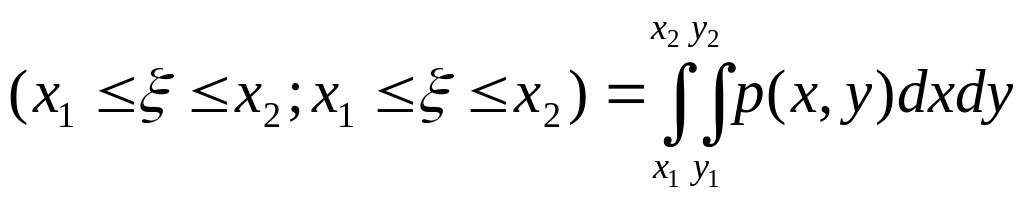

3.

4.

20.Независимость случайных величин.

Случайные величины ₁, ₂ называются независимыми, если для любых действительных чисел x₁,…,x_n R случайные события ( ₁<X₁),…, ( _n<X_n) независимы.

Из определения независимых событий вероятность появления должна равняться произведению вероятностей

P( ₁<X₁,…, _n<X_n )=P( ₁<X₁)…P( _n<X_n)

Случайные события независимы, если многомерная функция распределения равна произведению функций распределения координат.

1. Дискретные случайные величины будут независимы, если . для всех ,

2. Непрерывные случайные величины. Они описываются плотностью вероятности, которая равнв производной n порядка по произв. х_n

p(x,y)= Если случайные величины независимы, то .

21.Условный закон распределения.

Условным законом распределения случайной величины, входящий в систему ( называется ее закон распределения, вычисленный при условии, что принимает значение у.

Пусть ( - непрерывный вектор с плотностью вероятности p(x,y).

Пусть B=(y< < ∆y)

Тогда условная функция распределения случайной величины  при условии, что событие В произошло

Пользуясь формулой умножения имеем

P=

Функция называется условной функцией распределения случайной величины  при условии В.

Возьмем производную от (1), устремив при этом ∆y к 0.

Функция называется условной плотностью вероятности случайной величины при условии, что  равен у.

Из (2) следует аналогичная теорема умножения

Из можем получить непрерывный аналог формулы полной вероятности

Из (2) можно получить условную функцию распределения случайной величины  при условии, что  равен у.

22.Неравенство Чебышева. Сходимость случайных последовательностей.

В формулировке ЗБЧ используется понятие «сходимости случайных величин по вероятности».

Случайные величины ₁, ₂,…, _n, …сходятся по вероятности к величине A(случайной или неслучайной), если для любого вероятность события при стремится к единице, т.е. .

Сходимость по вероятности символически записывают так .

Неравенство Чебышева

Для случайной величины , имеющей ограниченную дисперсию , и для любого справедливо неравенство Чебышева

(14.1)

Док-во: Пусть .

Докажем неравенство (14.1) для непрерывной случайной величины с плотностью распределения . Вероятность есть вероятность попадания с.в. в область, лежащую вне промежутка [ ]. Можно записать

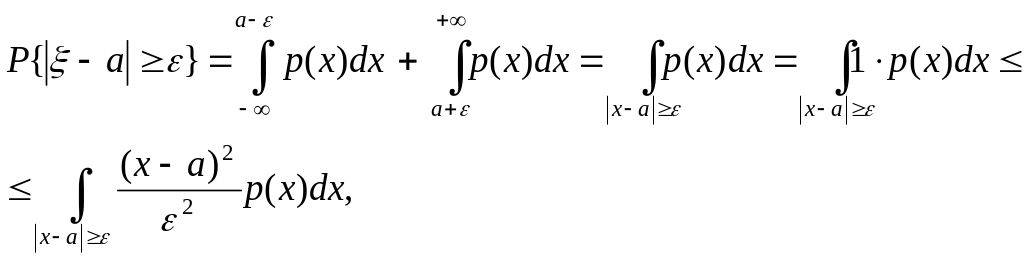
т.к. область интегрирования можно записать в виде . Имеем

т.к. интеграл от неотрицательной функции при расширении области интегрирования может возрасти.

Аналогично доказывается неравенство Чебышева и для дискретной случайной величины , только интегралы (вида ) заменяются соответствующими суммами (вида ).

Отметим, что неравенство Чебышева часто используется для противоположного события: