
- •1Случайные события. Действия над событиями.
- •2.Классическое опред. Вероятности и ее свойства.
- •3.Аксиоматическое определение вероятности.
- •5.Условная вероятность. Независимость событий.
- •6.Формула полной вероятности. Формула Байеса.
- •7.Схема независимых испытаний Бернулли.
- •8.Предельные теоремы в схеме Бернулли.
- •10.Плотность распред.Вероятностей и ее свойства.
- •11.Математическое ожидание и его свойства.
- •12.Дисперсия и ее свойства.
- •13.Коэффициент корреляции и ковариация.
- •14.Моменты.
- •15.Осн. Дискретные распред.Случайных величин.
- •16.Равномерное и показательное распределения. Равномерное распределение.
- •Показательное распределение.
- •17.Нормальное распределение.
- •18.Двумерная функция распред. И ее свойства.
- •19.Двумерная плотность вероятности и ее свойства.
- •20.Независимость случайных величин.
- •21.Условный закон распределения.
- •22.Неравенство Чебышева. Сходимость случайных последовательностей.
- •23.Теорема Чебышева. Теорема Бернулли.
- •24.Центральная предельная теорема.
- •25.Выборочный метод.
- •26.Эмпирическая функция распределения и ее свойства.
- •27.Гистограмма и полигон.
- •28.Числовые характеристики выборки.
- •29.Точечное оценивание
- •30.Доверительные интервалы
- •31.Распределения , Стьюдента и Фишера.
- •33.Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном .
- •34.Проверка статистических гипотез.
- •35.Построение критической области.
- •36.Критерий согласия Пирсона.
- •37.Вычисления теоретических частот для нормального распределения.
- •38.Сравнение дисперсий двух нормальных выборок.
- •39.Сравнение средних двух нормальных выборок (критерий Стьюдента).
- •40.Дисперсионный анализ.
- •41.Парная регрессия.
- •42.Парный коэффициент корреляции, его свойства.
- •43.Проверка гипотезы о достоверности выборочного коэффициента корреляции.
- •44.Нелинейная парная регрессия.
37.Вычисления теоретических частот для нормального распределения.
Пусть
имеется выборка
![]() объема n,
и есть основание предположить, что она
имеет нормальное распределение. Для
вычисления теоретических частот
необходимо выполнить действия, указанные
ниже.
объема n,
и есть основание предположить, что она
имеет нормальное распределение. Для
вычисления теоретических частот
необходимо выполнить действия, указанные
ниже.
находим
максимальное и минимальные значения
значение выборки, размах варьирования.
![]()
Для
определения количества интервалов
группировки k
воспользуемся формулой Стерджеса:![]() .
.
Тогда
ширину частичных интервалов
![]() находим из формулы
находим из формулы
![]() .
.
Число
k
округляется в сторону наибольшего
целого числа. Интервалы строятся таким
образом, чтобы
![]() и
и
![]() входили
внутрь интервалов. Для этого в качестве
левой границы первого интервала можно
взять
входили
внутрь интервалов. Для этого в качестве
левой границы первого интервала можно
взять
![]() ,
а в качестве правой границы последнего
интервала
,
а в качестве правой границы последнего
интервала
![]() .
В качестве частоты
вариационного
ряда записывают число наблюдений,
попавших в каждый
.
В качестве частоты
вариационного
ряда записывают число наблюдений,
попавших в каждый
![]() промежуток.
промежуток.
2.
Для того, чтобы получить оценки параметров
и
![]() перейдем
к дискретному ряду, взяв в качестве
варианты Х ряда середины построенных
интервалов
перейдем
к дискретному ряду, взяв в качестве
варианты Х ряда середины построенных
интервалов
![]() .
В итоге получим последовательность
равноотстоящих вариант и соответствующих
им частот:
.
В итоге получим последовательность
равноотстоящих вариант и соответствующих
им частот:
|
* |
* |
… |
|
|
|
|
… |
|
Несмещенной
оценкой матожидания является исправленное
выборочное среднее
![]() ,
а дисперсии – исправленная выборочная
дисперсия s2.
,
а дисперсии – исправленная выборочная
дисперсия s2.
![]() ,
,![]() или
или
![]() .
.
3. Нормируем случайную величину Х, перейдя к величинам
![]() и
и
![]() ,
,
![]() .
.
Причем
наименьшее значение
![]() будем
считать равным
,
а наибольшее значение -
будем
считать равным
,
а наибольшее значение -
![]() ,
так как теоретическое нормальное
распределение принимает значения на
числовой оси.
,
так как теоретическое нормальное
распределение принимает значения на
числовой оси.
4.
Вычислим теоретические вероятности pi
попадания
Х в интервалы
![]() :
:![]() ,
,
где
![]() ,
,
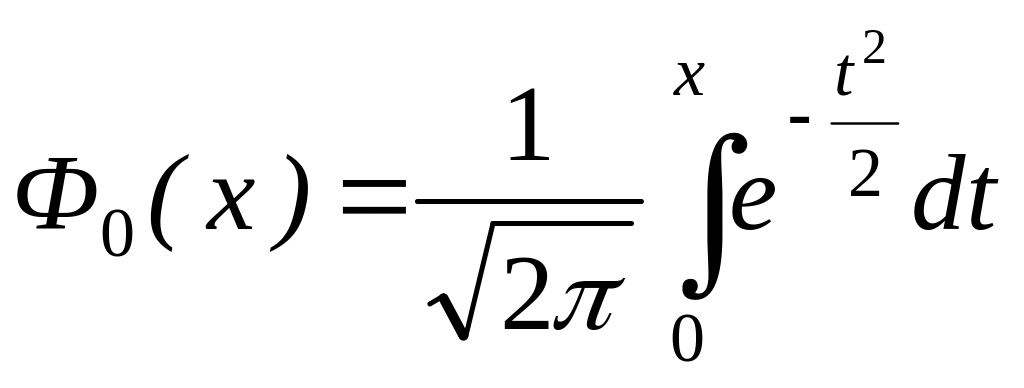 - функция Лапласа.
- функция Лапласа.
5.
Рассчитаем теоретические частоты
![]()
![]() .
.
Замечания
1 Т.к.норм распр принимает знач от до + то буде считать что
ф-ция Лапласа не четная и асимптотическая
38.Сравнение дисперсий двух нормальных выборок.
Рассмотрим несколько критериев однородности. Пусть имеется 2 выборки X и Y объемами n1 и n2 и пусть ставится задача сравнить их функции распределения.H0:F1(x)=F2(x)
Такого рода задания часто называют выявлением отклика на воздействия. Например, Наиболее хорошо разработанными являются методы выявления однородности для нормально распределенных выборок. Если выборки распределены нормально, то выявление однородности сводится к сравнению параметров а иσ. Эти методы называются параметрическими. Если о распределении изучаемых выборок ничего нельзя сказать, то применяются непараметрические методы, где не учитываются исходные количественные данные, а только уравнение <,>.
Пусть выборки X и Y распределены нормально с параметрами а1и σ1 ; а2 σ2соответсвенно.X~N(а1,σ 1), Y~N(а2,σ 2).
Гипотеза H0 будет справедлива, если будут равны параметры а1= а2; σ1=σ2
Сравним сначала дисперсии этих выборок H0: σ21=σ22
Несмещенной и состоятельной оценкой дисперсии является исправленная выборочная дисперсия.
![]()
![]()
Следующая гипотеза H0: S21=S22
Сравнение дисперсий всегда осуществляется путем вычисления их отношения. Можно показать, что при H0 эта случайная величина имеет распределение Фишера с k1 и k2 числом степеней свободы.
F=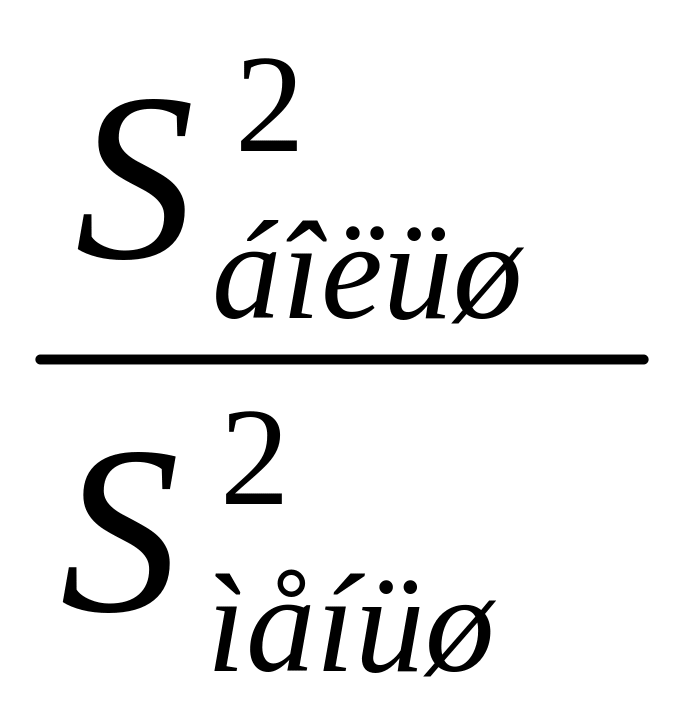 ~F(k1,k2)
Причем
k1=n1-1,
k2=n2-1,
S21>S22
~F(k1,k2)
Причем
k1=n1-1,
k2=n2-1,
S21>S22
Пусть H1: S21>S22, т.е. правосторонняя критическая область. Fk(Kкр)=1-α
Проверка H0 осуществляется следующим образом:
Вычисляется наблюдаемое значение критерия,
Выбирается уровень значимости αи по таблице критических точек распределения Фишера находят Fкр(α,k1,k2)
Если Fнабл> Fкр , то H0 отвергаем и принимаем конкурирующую.
2.
Пусть H1:
S21![]() S22
-. двусторонняя критическая область.
S22
-. двусторонняя критическая область.
В этом случае поступают аналогично, только Fкр(α/2,k1,k2)
