8.Предельные теоремы в схеме Бернулли.

При больших n применение формулы Бернулли затруднительно из-за сложности вычисления факториалов и степеней. В этом случае исп. приближенные формулы. Рассмотрим 2 случая:

1. или .

2. p (0,1) и не близко ни к нулю, ни к единице.

Теорема Пуассона.Если в схеме Бернулли , так, что np a, тогда

. Замечания:

1. – среднее число появления события А в n испытаниях.

2. Как правило, теорему Пуассона применяют, когда .

3. В конце книг по теор. вероятности есть таблицы для подсчета вероятности для различных a и m.

Локальная предельная теорема Муавра-Лапласа.

Если вероятность наступления некоторого события в n независимых испытаниях постоянна и равна p, p(0,1), то вероятность того, что в этих испытаниях событие A наступит ровно m раз, удовлетворяет при n соотношению

, где

Равномерно по всем m,для которых находится в каком-то конечном интервале;

Функция - плотность нормального распределения.

Интегральная предельная теорема Муавра-Лапласа.

Если m есть число наступлений события в n независимых испытаниях, в каждом из которых вероятность этого события равна p, причем p (0,1), то равномерно относительно a и b(−∞<a<b<+∞) n имеет место соотношение ,

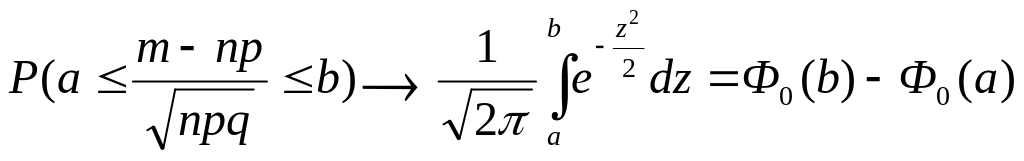Где 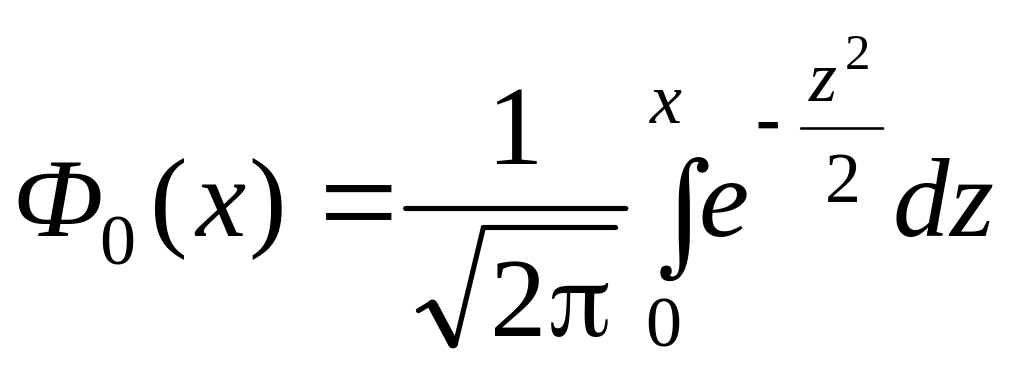- функция Лапласа.

Замечания.

1. Функция Лапласа нечетная:

= - .

2. Функция Ф₀(z) асимптотическая и при она быстро стремиться к 0,5. Это стремление настолько быстрое, что при можно считать равной 0,5.

3. Плотность нормального распределения - четная функция.

4. Функции , в конце книг по ТВ и МС заданы таблично.

9.Ф-ция распред.вероятностей и ее свойства.

Одним из осн.понятий теории вероятностей явл. случайная величина.Случайные величины бывают дискретные, непрерывные и др. Для того, чтобы одинаковым способом характ.случ. величины различной прир.вводится понятие ф-ции распред.вероятностей. Пусть - случайная величина и - произвольное действительное число. Вероятность того, что примет знач., меньшее чем х, наз.функцией распред. вероятностей: .Случайной наз.величина,знач.кот.зависят от случая и для кот.опред.ф-ция распред. вероятностей. Дискретной наз.случайная величина,кот.прин. конечное или счетное мн-во знач. Под счетным мн-вом понимается мн-во натуральных чисел.Счетное мн-во знач.можно пронумеровать: Для полной вероятностной хар-ки дискретной случ. величины необх.знать ее закон распред. Пусть –возможные знач.случайной величины , - вероятности этих знач.Мн-во пар , i =1,2,… наз.законом распред.вероятн.дискретной случ. величины. Обычно закон распред.изображ.в виде табл.:

					…
P					…

Непрерывной наз.случайная величина,знач.кот. заполняют сплошь некот.промежутки.Ф-ция распред.вероятностей явл.неслуч.ф-цией, вычисленной на основании закона распред. случ.величины.Св-ва функции распределения:

1. ,0 ,т.к. это вероятность.

2. – неубывающая ф-ция.

.Следствия:

2.1. Вероятность попадания случ.величины в заданный интервал есть приращение ф-ции распред. на этом интервале:

2.2. Вероятность принять одно фиксированное знач.для непрерывн.случ.величины равна нулю.

, при т.к. ф-ия распред.непрерывн.случайной величины непрерывна.

2.3Вероятн.попадания непрерывн.случ. велич. в открытый или замкнутый промеж. одинакова: Докажем последнее равенство

3. непрерывна слева в каждой точке (см. рис.7.1).

4.

5. .