
UMLE6-106_F
.pdfМинистерство образования РФ Ростовский государственный строительный университет
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
для студентов строительных специальностей
Ростов-на-Дону
2004
2
УДК 515
Начертательная геометрия: Учебник для студентов строительных специальностей. – Ростов н/Д: РГСУ, 2004.
Настоящий учебник составлен в соответствии с программой по начертательной геометрии для студентов строительных специальностей, утвержденной Министерством образования Российской Федерации.
В учебнике подробно изложены вопросы теории графических изображений и приведены примеры с решениями. Книга поможет студентам при минимальной затрате времени изучить курс начертательной геометрии, предусмотренный программой.
Научные редакторы: Стрижаков А.В., Мартиросов А.Л., Кубарев А.Е.
Ростовский государственный строительный университет, 2004 г.
3
ПРЕДИСЛОВИЕ
Данная книга является переработанным и исправленным вариантом учебного пособия по начертательной геометрии Наумович Н.В., Ведерникова Н.Л. и др., которое называлось «Теория графических изображений» и было выпущено издательством Ростовского инженерно-строительного института в 1976 году.
Вразработке нового учебника принимали участие все преподаватели кафедры начертательной геометрии и черчения Ростовского государственного строительного университета: заведующий кафедрой, доц., к.т.н. Кубарев А.Е.; доц., к.т.н. Мартиросов А.Л.; доц., к.т.н. Лисицын В.Ю.; доц., к.т.н. Замятин А.В.; старшие преподаватели Арцишевская О.А. и Ковалева Н.В.; ассистенты Стрижаков А.В., Пашян Д.А., Бандура Ю.Н., Палий Т.Г., Федорова А.В., Сухомлинова В.В.
Была проведена работа по:
1) корректировке структуры текста и принятых обозначений;
2) выполнению рисунков в программе AutoCAD, аналогичных тем, которые были выполнены вручную для учебного пособия 1976 года;
3) исправлению некоторых обозначений в тексте и на изображениях в соответствии с более правильными и принятыми для лекционного курса начертательной геометрии, читаемого преподавателями РГСУ.
Вучебнике приведены разделы полного курса начертательной геометрии, рассматривающие ортогональные, аксонометрические, перспективные проекции и проекции с числовыми отметками, а также тени в ортогональных, аксонометрических и перспективных проекциях. Этот курс изучается студентами строительных специальностей в РГСУ и других вузах России. Книга может представлять интерес для инженеров, проектировщиков строительных организаций, преподавательского состава кафедр начертательной геометрии различных учебных заведений.
ОБЩИЕ ПОЛОЖЕНИЯ
В основе теории и практики графических изображений лежит наука
«начертательная геометрия», являющаяся разделом геометрии, в кото-
ром пространственные формы изучаются при помощи их изображений на плоскости, а в отдельных случаях – на кривых поверхностях. Такие
изображения, выполненные по определенным правилам и с помощью специальных чертежных инструментов, называют чертежами.
Изучение теории графических изображений преследует три основных цели: 1) освоение методов построения на плоскости изображений про-

4
странственных форм, 2) исследование геометрических свойств фигур и тел по их изображениям и 3) развитие пространственного воображения.
Конструкторы, строители и механики должны свободно владеть этой теорией, дающей правила построения чертежей и развивающей умение понимать их.
Техника предъявляет к чертежам два основных требования: наглядность и хорошая измеримость. Таким требованиям удовлетворяют чертежи, построенные при помощи так называемого метода проецирования.
Метод проецирования состоит в том, что через точки, данные в пространстве и подлежащие изображению на какой-либо поверхности, проводят прямые (проецирующие линии или лучи) и находят точки пересечения этих прямых с заданной поверхностью. Полученные точки называют проекциями данных точек на заданной поверхности.
При проецировании находящиеся в пространстве точки принято обозначать прописными буквами латинского алфавита: А, B, C … или цифрами 1, 2, 3 …, а прямые – двумя буквами AB, CD …, цифрами 12, 34 … или малыми буквами a, b, c … Плоскости и поверхности будем обозначать прописными буквами греческого алфавита: , , , , , и др.* или несколькими буквами латинского алфавита, например АВС, КLМN и др. Плоскости, на которых строят изображения, называют плоскостями проекций и обычно обозначают заглавной буквой (пи) греческого алфавита, иногда с индексами ( 1, 2 …).
Для развития у студентов навыков быстрой записи геометрических понятий и описания выполняемых построений вводятся символы: – принадлежность, – включение, – объединение, – пересечение, = – соответствие, или результат операции соединения и пересечения, – совпадение**.
Таким образом, запись А b показывает, что точка А лежит на прямой b, запись a В означает, что прямая а проходит через точку В, запись а b = М выражает, что прямые а и b пересекаются в точке М, а
предложение: «Точки А и |
В соединяем прямой b» записывается так: |
||
А |
В = b. Запись А В означает, что точки А и |
В совпадают. Записи |
|
(а |
b) и (с d) означают, что плоскость |
задана пересекающимися |
|
прямыми а и b, а плоскость |
– параллельными с и d. |
||
§ 1. ВИДЫ ПРОЕЦИРОВАНИЯ
Существует два основных вида проецирования: центральное (кониче-
ское) и параллельное (цилиндрическое).
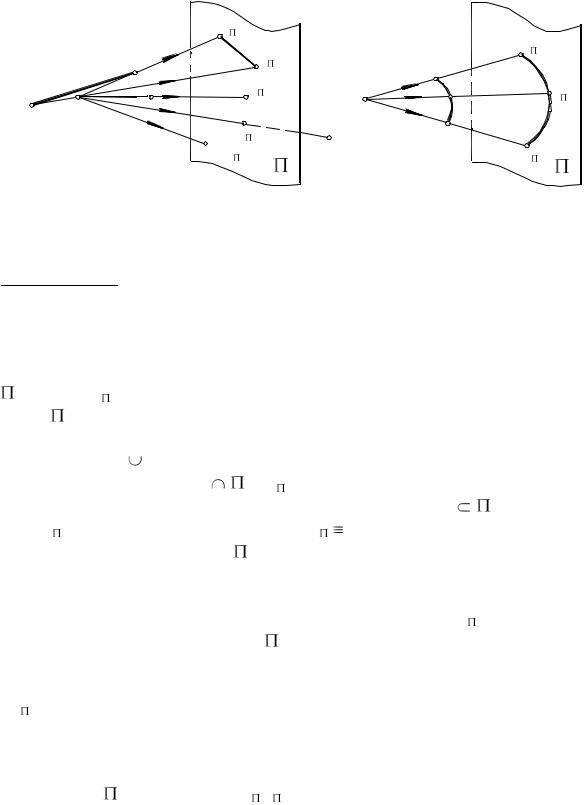
Центральное проецирование. Пусть в пространстве дана точка А и плоскость , на которую нужно ее спроецировать (рис. 1а). Выберем произвольную точку S – центр проецирования, не лежащую в плоскости ,
5
|
|
A |
|
|
|
|
|
B |
A |
|
A |
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
m |
m |
B |
B |
B |
S |
|
S |
|
|
|
|
|
|
|
|
C |
C |
|
|
|
D=D |
C |
C |
|
|
|
||
|
|
а) |
б) |
|
Рис. 1
*Наименование этих букв соответственно: гамма, тэта, каппа, пи, пси, омега.
**Эти символы необходимо хорошо запомнить, иначе чтение настоящей книги будет затруднительным.
ипроведем прямую SА (проецирующий луч) до пересечения с плоскостью
вточке А . Эта точка будет центральной проекцией точки А на плос-
кость . Таким образом, для получения центральной проекции точки выполняются две операции: 1) заданную точку соединяют прямой с центром
проекций S (А |
S = AS), 2) находят точку пересечения этой прямой с |
||
плоскостью проекций (AS |
= A ). |
|
|
Если точка D принадлежит плоскости проекций (D |
), то ее проек- |
||
ция D совпадает |
с самой |
точкой (D D). На рис. 1а |
показано также |
проецирование на плоскость |
точек B и C и прямых АВ и m. |
||
Чтобы спроецировать прямую АВ, не проходящую через точку S, нужно через эту точку и заданную прямую провести плоскость SAB, называемую проецирующей плоскостью, и найти прямую А В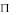 пересечения этой плоскости с плоскостью . Найденная прямая и будет искомой проекцией.
пересечения этой плоскости с плоскостью . Найденная прямая и будет искомой проекцией.
Если прямая m проходит через точку S, то она проецируется в точку
(m ).
Проекцией кривой АВС называют совокупность проекций всех ее то-
чек. Проецирующие лучи, проведенные через все точки этой кривой, обра-
зуют проецирующую коническую поверхность, пересечение которой с плоскостью дает кривую А В С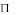 – центральную проекцию заданной кривой (рис 1б).
– центральную проекцию заданной кривой (рис 1б).
Плоская фигура проецируется в общем случае в плоскую фигуру. В частном случае, если плоскость фигуры проходит через центр проекций, то фигура проецируется в отрезок прямой.
6
Изображения, полученные с помощью центрального проецирования, обладают наилучшей наглядностью, но наихудшей измеримостью.
Параллельное проецирование. В практике широко применяется параллельное проецирование, являющееся частным случаем центрального проецирования, при котором центр проецирования – точка S удалена в
|
|
B |
|
|
B |
|
S |
|
A |
M |
M |
|
|
|
|
S |
|
|
|
A |
С =С |
|
|
|
|
|
|
|
а) |
|
б) |
Рис. 2
бесконечность. В этом случае проецирующие лучи параллельны между собой.
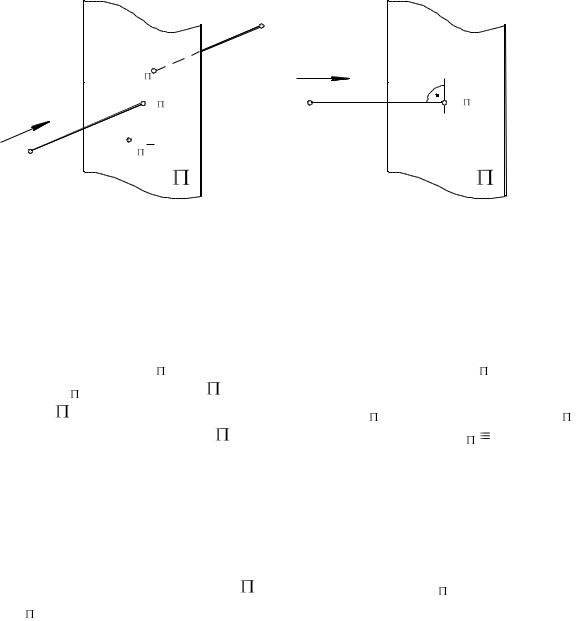
На рис. 2а даны точки А, В, С и направление проецирования s, которое не должно быть параллельно плоскости проекций. Проведем через точку А
проецирующий луч АА параллельно направлению s. Точка А |
пересече- |
||
ния луча АА |
с плоскостью |
дает параллельную проекцию точки А на |
|
плоскость . |
Аналогично построена проекция В точки В. Проекция С |
||
точки С, лежащей в плоскости |
, совпадает с самой точкой (С |
С). |
|
Параллельные проекции обладают несколько меньшей наглядностью,
но лучшей измеримостью, чем центральные. Когда поверхностью проекций является плоскость, параллельное проецирование разделяют на ортогональное (прямоугольное) и косоугольное.
Ортогональным называют такое проецирование, при котором про-
ецирующие прямые перпендикулярны плоскости проекций. В этом случае проекцией точки М на плоскость является основание М перпендикуляра ММ , опущенного из точки М на плоскость проекций (рис. 2б).
Если направление проецирования не перпендикулярно плоскости про-
екций, то проецирование называют косоугольным.
Большинство технических чертежей строится методом ортогонального проецирования. Этот метод обладает наилучшей из-
меримостью, но наихудшей наглядностью.
§ 2. ОСНОВНЫЕ СВОЙСТВА ПАРАЛЛЕЛЬНОГО
ПРОЕЦИРОВАНИЯ
7
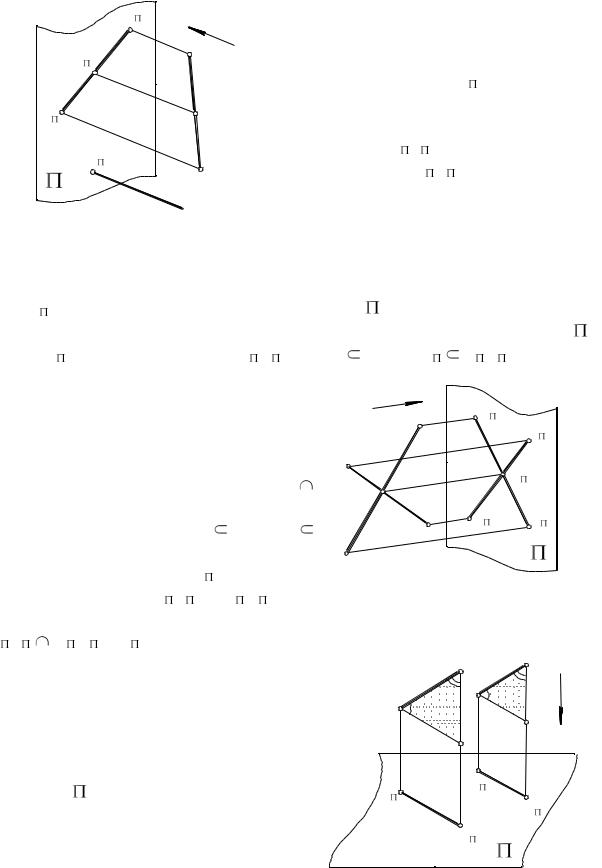
1. Проекция точки – точка, проекция прямой – прямая. Прямая линия
(рис. 3), если она не параллельна направлению проецирования, проецируется в прямую, так как все лучи, проецирующие точки А, В и С, лежащие
на этой прямой, |
расположены |
в одной проецирующей плоскости, |
|
|
|
которая пересекается с плоскостью |
|
C |
S |
проекций по прямой. В частном слу- |
|
|
чае, если прямая n параллельна на- |
||
|
|
||
B |
C |
правлению проецирования, то она |
|
|
|
проецируется в точку (n ). |
|
A |
B |
Плоскость, параллельная направ- |
|
лению проецирования, например, |
|||
|
|
||
n |
|
плоскость АСС А на рис. 3, проеци- |
|
A |
руется в прямую А С . |
||
|
|||
|
n |
2. Если точка лежит на прямой, |
то проекция этой точки лежит на
Рис. 3 |
|
|
|
соответствующей |
проекции данной |
|
|||||
прямой. |
Действительно, пусть точка В лежит на прямой АС (рис. 3), тогда |
||||||||||
луч ВВ , проецирующий точку В на плоскость |
, принадлежит плоскости, |
||||||||||
проецирующей прямую АС и, следовательно, пересекается с плоскостью |
|||||||||||
в точке В , лежащей на прямой А С |
(если В |
АС, то В |
А С ). |
|
|||||||
3. Если заданные прямые пересека- |
|
|
|
|
|||||||
ются, то их проекции тоже пересека- |
|
S |
A |
|
|||||||
ются, причем точка пересечения проек- |
|
A |
|
||||||||
|
|
C |
|||||||||
ций есть |
проекция точки |
пересечения |
|
|
|
||||||
C |
|
|
|
||||||||
данных прямых. Пусть прямые АВ и CD |
|
|
|
||||||||
|
|
K |
|
||||||||
(рис. 4) |
пересекаются в точке К (АВ |
|
|
|
|||||||
|
K |
|
|
||||||||
CD = К), тогда К принадлежит одновре- |
|
|
|
||||||||
|
|
D |
B |
||||||||
менно прямым АВ и CD (К |
АВ и К |
|
D |
||||||||
|
|
|
|||||||||
CD), а поэтому |
на |
основании |
пре- |
B |
|
|
|
||||
дыдущего пункта точка К |
будет при- |
|
|
|
|||||||
|
|
|
|
||||||||
надлежать прямым А В |
и С D , |
т.е. |
|
|
|
|
|||||
совпадать |
с точкой |
их |
|
пересечения |
|
|
Рис. 4 |
|
|||
(А В |
С D = К ). |
|
|
|
|
|
|
|
D |
||
4. Проекции двух параллельных от- |
|
|
B |
||||||||
|
|
|
|||||||||
резков прямых параллельны между со- |
|
A |
C |
S |
|||||||
бой и отношение длин этих проекций |
|
|
|
||||||||
равно отношению длин самих отрезков. |
|
|
|
E |
|||||||
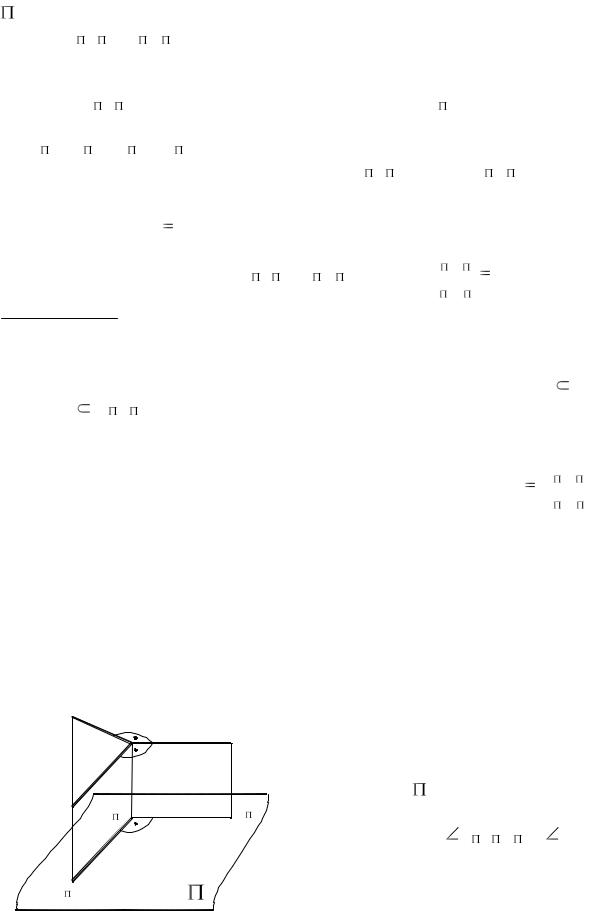
Пусть АВ CD (рис. 5), тогда две плос- |
|
|
F |
|
|||||||
кости, |
проецирующие |
эти |
отрезки на |
|
|
C |
|
||||
плоскость |
, будут также параллельны |
|
A |
|
|||||||
|
|
|
|||||||||
и, как известно из геометрии, пересекут- |
|
|
|
D |
|||||||
|
|
|
|
|
|
|
|
|
|
B |
|
8 |
|
ся с третьей плоскостью (с плоскостью |
|
) по параллельным прямым. Эти |
|
прямые А В и С D и будут проекция- |
|
ми заданных прямых. |
Рис. 5 |
В плоскости, проецирующей отрезок АВ, проведем через точку А прямую AF А В до пересечения в точке F с прямой ВВ (рис. 5). Аналогичное построение выполним в плоскости, проецирующей отрезок CD. Фигуры А АFВ и С СЕD в общем случае параллельного проецирования бу-
дут параллелограммами*, а поэтому AF = А В и |
СЕ = С D . Треуголь- |
|||||||
ники ABF и CDE подобны, так как соответственные углы у них равны. |
||||||||
Следовательно |
AF |
|
AB |
. Заменив в этом равенстве AF и CE соответст- |
||||
|
|
|||||||
|
CE |
|
CD |
|
|
|
|
|
венно равными им отрезками А В и С D , получим |
A В |
|
AB |
. |
||||
|
|
|||||||
|
|
|
|
|
C D |
|
CD |
|
* При ортогональном проецировании эти фигуры обращаются в прямоугольники.
5. Если точка делит отрезок прямой в каком-то отношении, то ее проекция делит проекцию отрезка в том же отношении. Пусть В АС,
тогда В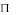 А С (рис. 3). Отрезки АВ и ВС можно рассматривать как параллельные между собой, но расположенные таким образом, что конец одного из них совпадает с началом другого. Следовательно, к этим отрезкам
А С (рис. 3). Отрезки АВ и ВС можно рассматривать как параллельные между собой, но расположенные таким образом, что конец одного из них совпадает с началом другого. Следовательно, к этим отрезкам
и их проекциям применимо только что доказанное свойство: |
AВ |
|
A B |
. |
|
|
|||
|
ВС |
|
В С |
|
Так как ортогональное проецирование есть частный случай параллель-
ного, то рассмотренные свойства справедливы и при ортогональном
проецировании.
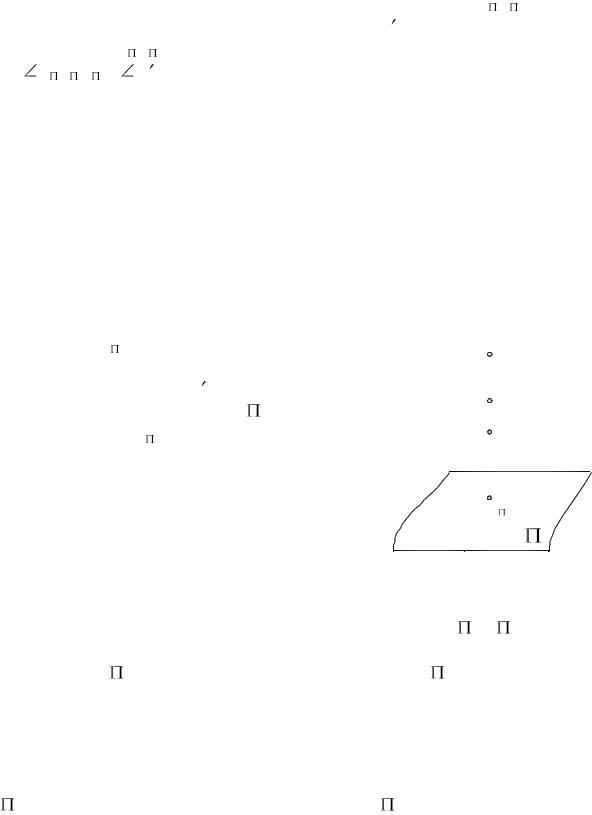
6. При ортогональном проецировании прямой угол проецируется в прямой тогда, когда одна сторона его параллельна плоскости проекций, а
A' |
|
|
другая не перпендикулярна этой плос- |
||
|
|
кости (теорема о проецировании пря- |
|||
|
|
|
|||
|
B |
C |
мого угла). На рис. 6 дан прямой угол |
||
|
|
||||
|
|
|
АВС, лежащий в плоскости, параллель- |
||
A |
|
|
ной плоскости . Естественно, |
что на |
|
B |
C |
эту плоскость он проецируется в нату- |
|||
|
|||||
|
|
|
ральную величину ( А В С = |
АВС). |
|
|
|
|
Если заданный угол повернуть вокруг |
||
A |
|
|
одной из его сторон, например, ВС, то |
||
|
|
|
|
||
|
|
|
9 |
|
|
|
|
сторона АВ переместится в проеци- |
|
|
|
|
рующей плоскости АВВ А |
в новое |
|
|
Рис. 6 |
положение А В, но ее проекция останет- |
|
ся |
прежней |
(А В ), |
следовательно, проекция угла также не |
изменит- |
ся( |
А В С |
= А ВС). |
|
|
Г Л А В А I
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ, ПРЯМОЙ, ПЛОСКОСТИ
§ 3. ПРОЕКЦИИ ТОЧКИ
Как уже сказано в § 1, ортогональной проекцией точки на плоскость является основание перпендикуляра, опущенного из данной точки на эту плоскость. Следовательно, любая точка, например точка В на рис. 7, при проецировании ее на плоскость имеет вполне определенную единственную
проекцию (В ). Однако данной проекции |
|
B |
||||
соответствует бесчисленное множество то- |
|
|
|
|||
чек в пространстве: В, В и т.д., |
лежащих на |
|
B' |
|||
перпендикуляре к плоскости |
, восстанов- |
|
||||
|
|
|
||||
ленном в точке В . Поэтому одна проекция |
|
B'' |
||||
|
||||||
|
|
|
||||
точки не определяет ее положения в про- |
|
|
|
|||
странстве. Для того чтобы определить по- |
|
|
|
|||
ложение точки в пространстве нужны до- |
|
B |
||||
|
||||||
полнительные данные, например, проекция |
|
|||||
|
|
|
||||
на другую плоскость. Обычно проецирова- |
|
|
|
|
||
ние ведут |
на две взаимно перпенди- |
|
|
|
||
кулярные плоскости проекций. Две проекции |
Рис. 7 |
|||||
точки вполне определяют ее положение в пространстве. |
|
|
|
|||
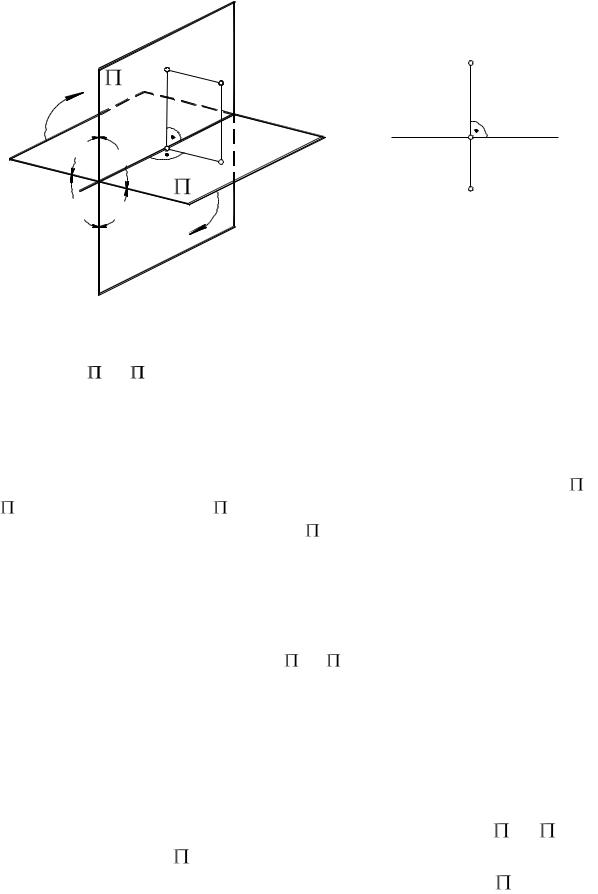
Возьмем две взаимно перпендикулярные плоскости 1 и 2 (рис. 8а). |
||||||
Одну из них ( |
1) называют горизонтальной, другую ( |
2) – фронтальной |
||||
плоскостями проекций. Линию их пересечения х называют осью проекций.
Эта ось разделяет каждую из плоскостей проекций на две полы: плоскость
1 – на переднюю и заднюю полы, плоскость 2 – на верхнюю и нижнюю
полы.
10
|
A2 |
A |
A2 |
|
|
|
|
||
|
2 |
|
|
|
II |
Ax |
x |
Ax |
|
I |
||||
|
A1 |
|
||
|
|
|
||
x |
1 |
|
A1 |
|
III |
IV |
|
|
а) |
б) |
|
Рис. 8 |
Плоскости ( 1 и 2) разделяют все пространство на четыре части, называемые четвертями или квадрантами: I, II, III и IV. Первой считают ту четверть, в которой находится наблюдатель, второй – четверть, расположенную за верхней полой фронтальной плоскости, третьей – расположенную под второй, а четвертой – под первой.
Пусть точка А расположена в первой четверти. Спроецируем ее на 1 и 2. Проекцию точки А на 1 обозначим А1 и назовем ее горизонтальной проекцией. Проекцию той же точки на 2 обозначим А2 и будем называть
фронтальной проекцией.
Проецирующий луч АА1 называют горизонтально проецирующей прямой, а АА2 – фронтально проецирующей прямой. Проецирующие прямые,
проведенные через точку А, определяют плоскость АА1А2, перпендикулярную к плоскостям проекций и к линии их пересечения – оси проекций x. Эта плоскость пересекает плоскости 1 и 2 по прямым А1Аx и АxА2, которые образуют с осью x и друг другом прямые углы.
Справедливо и обратное положение: если на плоскостях проекций даны точки А1 и А2, расположенные на прямых, пересекающих ось x в одной точке Аx под прямым углом, то данные две точки являются проекциями некоторой точки А. Эта точка опре-
деляется пересечением перпендикуляров, |
|
восставленных из точек А1 и А2 к плоскостям проекций |
1 и 2. |
Если плоскость 1 повернуть вокруг оси x так, чтобы ее пе- |
|
редняя пола совместилась с нижней полой плоскости |
2, то по- |
