
UMLE6-106_F
.pdf
|
|
|
127 |
|
|
|
|
§ 49. ПРОЕКЦИИ ТОЧЕК И ПРЯМЫХ. ВЗАИМНОЕ |
|||||||
ПОЛОЖЕНИЕ ПРЯМЫХ |
|
||||||
На рис. 159а приведен «профиль» (разрез) ярко выраженного рельефа |
|||||||
местности, на котором выбрано три точки А, В и С. На том же рисунке по- |
|||||||
казан фронтальный след плоскости |
, принятой за нулевую. Точка А нахо- |
||||||
дится выше плоскости |
на 4 м, точка В – ниже этой плоскости на 2 м и |
||||||
точка С лежит в плоскости |
. На рис. 159б приведены заданные точки в |
||||||
|
|
A |
|
|
|
|
|
а) |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
С |
0 |
|
|
|
|
|
|
|
B |
б) |
|
|
|
|
|
|
|
|
|
A4 |
|
|
|
С |
B-2 |
|
|
|
|
|
|
0 |
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Рис. 159 |
|
|
|
|
|
|
|
* Часто проекции точек обозначают только цифрами, соответствую- |
|||||||
щими их высотам, без букв. |
|
|
|
|
|
|
|
проекциях с числовыми отметками: А4, В-2 |
и С0*. На том же рисунке при- |
||||||
веден масштаб с целью облегчения измерения расстояний на проекции. |
|||||||
Такой профиль является наглядным, если расстояния проецируемых точек |
|||||||
до пл. и между собой – величины одного порядка, но если высоты малы, |
|||||||
а расстояния между точками велики, изображение становится неприемле- |
|||||||
мым. |
|
|
|
|
|
|
|
Прямая может быть задана 1) проекциями с числовыми отметками |
|||||||
двух ее точек или 2) одной точкой с числовой отметкой, направлением го- |
|||||||

128
ризонтальной проекции этой прямой и тангенсом угла ее наклона к пл.
**.
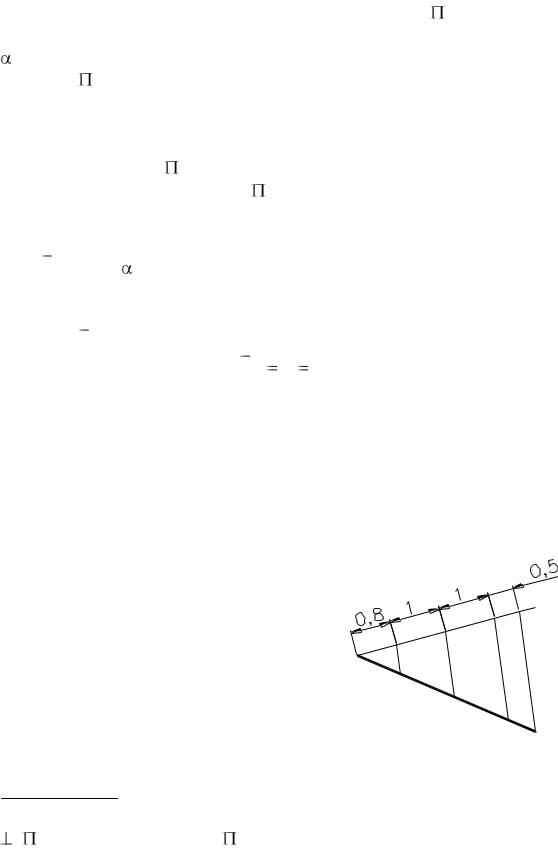
На рис. 160а показаны для наглядности две точки А и В в пространстве с их проекциями на пл. и приведены проекции А3 и В5 этих точек с числовыми отметками. Соединив прямыми точки А и В, а также проекции А3 и В5, получим отрезок прямой АВ в пространстве и его проекцию с числовыми отметками – А3В5. Эта проекция вполне определяет отрезок АВ в пространстве.
|
|
B |
|
|
A |
|
hB |
A3 |
B5 |
|
|
|||
|
|
|
||
hA |
L |
B5 |
|
н. в. |
|
|
|
||
|
|
|
B' |
|
A3 |
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
|||||||
L |
B5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A3
а) |
б) |
Рис. 160
* Отметка точки, находящейся ниже пл. , считается отрицательной и проставляется со знаком «минус».
** Если прямая от заданной точки поднимается, тангенс угла считается положи-
тельным.
129
Для нахождения натуральной величины отрезка АВ, заданного его проекцией с числовыми отметками, следует мысленно построить в пространстве прямоугольную трапецию А3АВВ5 (рис. 160а) и повернуть ее вокруг проекции А3В5 до совмещения с плоскостью . Противоположная А3В5 сторона трапеции выразит искомую натуральную величину АВ, а угол
между натуральной величиной АВ и А3В5 – угол наклона заданной прямой к пл. .
Вместо трапеции обычно строят прямоугольный треугольник (рис. 160б), одним катетом которого является заданная проекция отрезка (в данном случае А3В5), а вторым – отрезок, равный разности расстояний концов
этого отрезка до пл. (в данном случае В5В = В5В – А3А = 5 – 3 = 2 м). Расстояния точек А и В от обозначают через hА и hВ (рис. 160а) и на-
= В5В – А3А = 5 – 3 = 2 м). Расстояния точек А и В от обозначают через hА и hВ (рис. 160а) и на-
зывают превышением этих точек над нулевой плоскостью, а длину проек-
ции отрезка (А3В5) – через L и называют заложением. Отношение i =
= |
|
|
hA |
hB |
= tg |
называют уклоном |
прямой, а величину, обратную ей, l = |
|||||||||||
|
|
|
L |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
1 |
= |
|
L |
|
– интервалом прямой. В рассматриваемом случае hA = 3 м, |
|||||||||||
|
|
hA |
hB |
|||||||||||||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
||||
hВ = 5 м, L = 7 м, тогда i = |
|
5 |
|
3 2 |
|
|
1 |
, т.е. прямая имеет уклон 1 : 3,5. |
||||||||||
|
7 |
|
|
7 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
3,5 |
||||||||
Интервал этой прямой l = |
3,5 |
|
= 3,5, а это значит, что если на рассматри- |
|||||||||||||||
1 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ваемом отрезке взять две точки, разность превышений которых равна 1 м, то заложение этого участка будет l = 3,5 м*.
Прямая может быть задана точками, имеющими дробные числовые отметки, а для решения целого ряда задач удобно иметь отметки точек
прямой, выраженные целыми числами. |
|
|
|
|
|
|
Отыскание на проекции задан- |
|
|
|
|
|
|
ного отрезка точек, отметки кото- |
|
|
|
|
|
|
рых равны целым числам и отли- |
|
|
|
|
|
|
чаются на единицу от отметок рас- |
|
|
|
6' |
6,5' |
|
сматриваемых соседних точек, на- |
|
|
5' |
|
||
|
4' |
|
|
|||
зывается градуированием |
прямой. |
A3,2 |
|
|
|
|
4 |
|
|
|
|||
Пусть задан отрезок прямой А3,2В6,5 |
|
|
|
|
||
(рис. 161), требуется его програ- |
|
|
5 |
|
|
|
дуировать. Через точку А3,2 прове- |
|
|
|
6 |
B6,5 |
|
дем произвольную прямую и на ней |
|
|
|
|
||
от этой точки отложим в любом |
|
Рис. 161 |
|
|
||
* Уклон i и интервал l прямой могут изменяться от 0 до ∞: если АВ |
||||||
, i = ∞, l = 0, если АВ |
, i = 0, а l = ∞. |
|
|
|
|
|

130
масштабе отрезок, равный разности между ближайшей целой отметкой и
отметкой точки А, т.е. А3,24′ = 4 – 3,2 = 0,8 м. Далее на той же прямой и в том же масштабе нужно отложить отрезки 4′5′ = 5′6′ = 1 м и последний от-
резок, равный разности между отметкой точки В и предыдущей целой отметкой, т.е. отрезок 6′6,5′ = 6,5 – 6 = 0,5 м. Полученную точку 6,5′ нужно соединить с В6,5 и через точки 4′ и 5′ провести прямые, параллельные прямой 6,5′В6,5. Эти прямые пересекут заданную проекцию А3,2В6,5 в искомых точках 4 и 5.
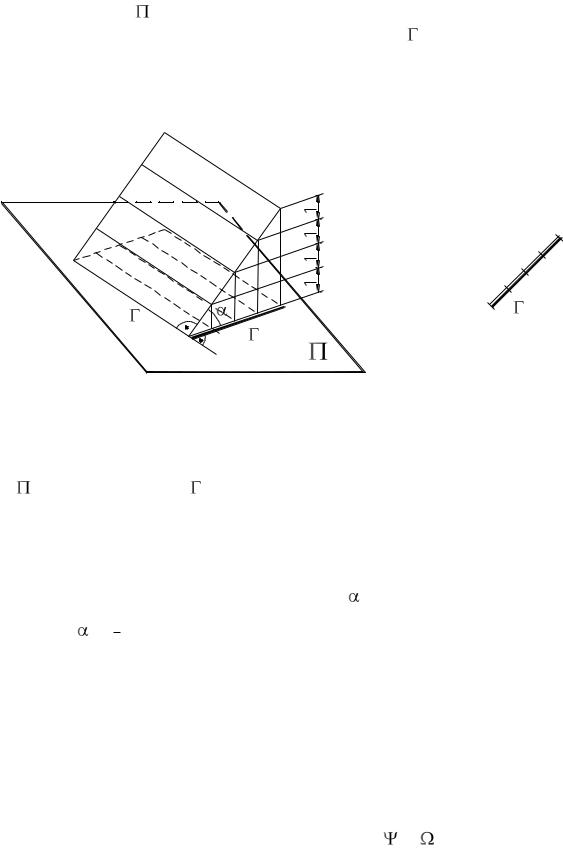
Две прямые в пространстве, как известно, могут быть взаимно парал-
лельными, пересекающимися и скрещивающимися. В первом случае проек-
ции обеих прямых будут взаимно параллельны, их интервалы равны между собой, а отметки должны возрастать в одном направлении (рис. 162а). Во втором случае проекции обеих прямых пересекаются и отметка точки пересечения должна быть одной и той же, независимо от того, к какой из прямых эта точка отнесена (рис. 162б).
Если хотя бы один из признаков взаимной параллельности или взаимного пересечения прямых не соблюдается, то данные прямые скрещивают-
ся (рис. 162в).
|
|
|
|
|
F3 |
|
M9 |
P6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
S8 |
|
|
|
|
|
|
|
|
|
|
C8 |
|
G2 |
|
|
|
|
|
|
5 |
|
3 |
4 |
|
|
K4 |
|
7 |
||
|
7 |
|
5 |
6 |
7 |
||||
|
|
|
|
||||||
|
|
|
|
|
H7 |
|
|
||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q4 |
|
A5 |
5 |
|
|
5 |
|
|
5 |
N6 |
|
D4 |
|
|
|
|
6 |
||||
|
4 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
6 |
R5 |
|
|
|
E 6 |
|
|
|
|
||
|
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L7 |
|
а) б) в)
Рис. 162
§ 50. ПРОЕКЦИИ ПЛОСКОСТЕЙ. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
Плоскость в проекциях с числовыми отметками может быть задана любым известным способом (точками, прямыми или их сочетанием), но
наиболее удобным является задание градуированной линией ската (см. §
10).
|
|
|
|
131 |
|
Проекцию на |
такой линии называют масштабом уклона плоскости. |
||||
На рис. 163а изображена в пространстве плоскость |
с линией ската 0IV и |
||||
горизонталями 0, I, II …, отстоящими друг от друга по высоте на 1 м. На |
|||||
|
IV |
|
|
|
|
III |
|
|
|
|
|
II |
|
|
|
IV |
|
|
|
|
|
|
|
I |
|
|
III |
|
4 |
|
|
|
|
|
3 |
0 |
|
II |
|
|
2 |
|
I |
|
|
|
1 |
|
2 |
3 |
4 |
0 |
|
0 |
1 |
|
i |
||
|
|
|
|
||
|
0 |
|
i |
|
|
|
|
|
|
|
|
а) |
б) |
|
Рис. 163 |
пл. показана проекция i, линии ската, т.е. масштаб уклона. На рис. 163б масштаб уклона приведен отдельно. Он изображается двумя параллельными прямыми, тонкой и утолщенной, пересеченными отрезками проекций указанных горизонталей. Расстояния между этими проекциями называются интервалами плоскости. Зная, что превышение точек первой горизонтали h = 1 м, а интервал равен l, легко найти угол наклона данной плоскости к
нулевой: tg = 1l . Этот же угол можно найти графически, построив прямо-
угольный треугольник, один катет которого равен 1, а другой – l.
Две плоскости в пространстве, как известно, могут быть взаимно параллельными или пересекающимися.
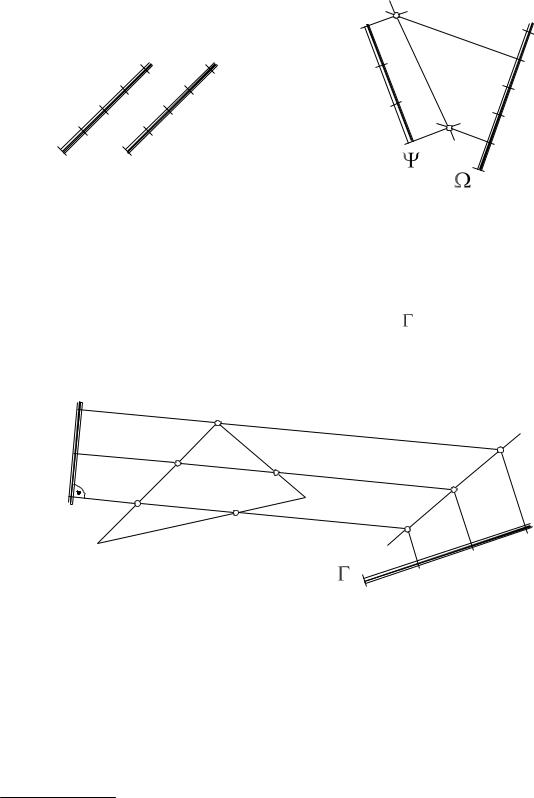
Параллельные между собой плоскости имеют взаимно параллельные масштабы уклона, с равными интервалами и возрастанием (или убыванием) отметок в одном направлении (рис. 164а). Если масштабы уклона заданных плоскостей не удовлетворяют хотя бы одному признаку взаимной параллельности плоскостей, то такие плоскости пересекаются. На рис. 164б приведены две пересекающиеся плоскости и и построена линия их пересечения. Эта линия в пространстве проходит через точки пересечения горизонталей, принадлежащих обеим плоскостям и расположенных на одной высоте. Например, горизонтали с отметкой 3 обеих плоскостей пе-
132
ресекаются в точке А, а горизонтали с отметкой 6 – в точке В. Прямая АВ и будет линией пересечения заданных плоскостей, а А3В6 – ее проекцией.
|
|
|
|
B6 |
|
|
6 |
11 |
6 |
|
7 |
|
5 |
|
6 |
||
|
5 |
10 |
|
||
|
|
5 |
|||
4 |
|
9 |
4 |
A3 |
|
3 |
8 |
|
4 |
||
|
|
||||
2 |
7 |
|
3 |
|
3 |
|
|
|
|
||
|
|
|
|
i |
2 |
|
|
|
|
i |
|
|
а) |
|
|
б) |
|
Рис. 164
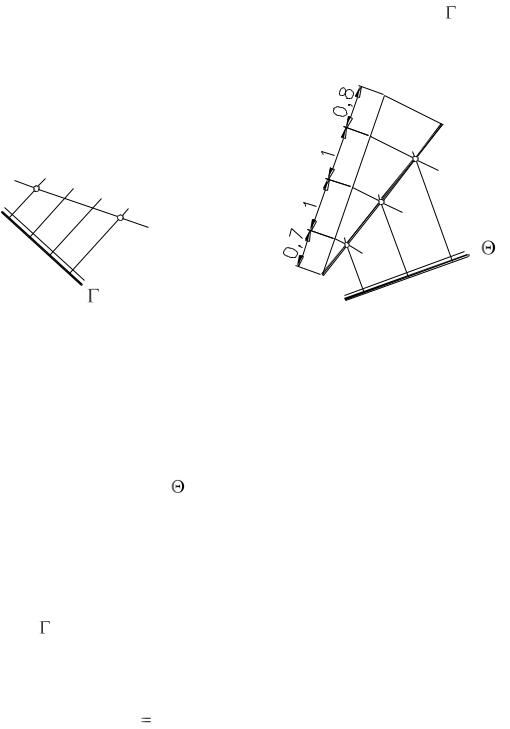
ПРИМЕР 73. Построить проекцию линии пересечения двух плоскостей, одна из которых задана масштабом уклона i, а вторая – тремя точками А6, В3 и С4,5 (рис. 165).
3 |
|
|
B3 |
|
|
|
4 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
5 |
5 |
|
C4,5 |
|
|
M4 |
|
|
|
5 |
|
N5 |
3 |
|
A6 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
i |
6 |
|
|
|
|
|
|
|
|
Рис. 165
Решение. Проградуируем прямые АВ, ВС и АС* и через точки с одинаковыми отметками (4 и 5) проведем прямые. Это будут проекции горизонталей второй плоскости. Проведем проекции горизонталей с теми же отметками, но принадлежащих первой плоскости. Проекции горизонталей, имеющих отметку 4, пересекаются в точке М4, а имеющих отметку 5 – в точке N5. Прямая М4N5 и будет искомой проекцией линии пересечения заданных плоскостей.
* См. § 49, рис. 161.
133
§51. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
1.Прямая лежит в плоскости, если она имеет с этой плоскостью по крайней мере две общие точки.
ПРИМЕР 74. В плоскости, заданной масштабом уклона i, провести прямую АВ общего положения (рис. 166).
|
|
|
|
|
B5,8 |
|
|
B9 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
4 |
9 |
|
A6 |
|
3 |
|
|
8 |
|
|
||
|
|
|
|
i |
|
|
|
7 |
A2,3 |
|
5 |
|
|
6 |
3 |
4 |
|
|
|
i |
|
|
Рис. 166 |
Рис.167 |
Решение. На любых двух горизонталях заданной плоскости (напри- |
|
мер, 6 и 9) выберем две произвольные точки (А6 |
и В9), соединяющая их |
прямая (А6В9) и будет искомой проекцией прямой АВ. |
|
ПРИМЕР 75. Проверить, принадлежит ли прямая А2,3В5,8 плоскости, |
|
заданной масштабом уклона i (рис. 167).
Решение. Проградуируем заданную прямую. Так как проекции точек прямой, имеющих отметки 3, 4, 5…, попали на проекции горизонталей плоскости с теми же отметками, то указанные точки будут общими и для прямой, и для плоскости, следовательно, прямая лежит в плоскости.
ПРИМЕР 76. Через точку А, лежащую в плоскости, заданной масшта-
бом уклона i, провести в этой плоскости прямую с уклоном i = |
2 |
|
(рис. |
|||||
3 |
|
|||||||
|
|
|
|
|
|
|
||
168). |
|
|
|
|
|
|
|
|
Решение. Чтобы провести прямую заданного уклона, нужно найти ин- |
||||||||
тервал этой прямой l = |
1 |
|
3 |
. Из заданной точки А3 радиусом r = l = |
3 |
м (в |
||
|
|
|
|
|||||
|
i |
2 |
|
2 |
|
|||
масштабе чертежа) сделаем засечки на проекциях двух ближайших горизонталей: с отметками 2 и 4. Полученные точки В2 и С4 будут лежать на искомой прямой. Кроме прямой ВС, будет еще одна прямая DE, удовле-

134
 C4
C4
i
A3  E4 5
E4 5
D2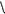 r 4
r 4
B2 |
3 |
|
2 |
||
|
A2
 3
3
L = 3,6
|
2 |
|
3 |
4 |
4 |
|
 5
5  B5 i
B5 i
Рис. 168 Рис.169
творяющая тому же условию*.
ПРИМЕР 77. Дана прямая А2В5, заложение которой L = 3,6 м. Через эту прямую требуется провести одну из двух возможных плоскостей ( ) с
уклоном iпл = |
4 |
(рис. 169). |
|
|
|
|
|
||||
|
|
|
|
|
|
||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
Решение. Найдем интервалы: а) прямой lпр = |
L |
3,6 |
= 1,2 м и |
||||||||
|
|
|
|||||||||
hB hA |
5 2 |
||||||||||
б) плоскости lпл = |
1 |
|
3 |
|
= 0,75 м. Проградуируем прямую. Через каждую |
||||||
iпл |
4 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
ее отметку должны проходить горизонтали искомой плоскости с теми же отметками. Расстояния между горизонталями lпл = 0,75 м. Чтобы найти направление этих горизонталей, из любой точки заданной прямой с целой отметкой (например, 3) опишем окружность радиуса lпл = 0,75 м и проведем к ней одну (любую) касательную из точки с отметкой на единицу меньшей (2) или большей (4). Проекции всех горизонталей, проходящих через точки 2, 3, 4 …, будут параллельны этой касательной**. Масштаб уклона i может быть построен в любом месте чертежа перпендикулярно направлению найденных проекций горизонталей.
* Если интервал прямой больше интервала плоскости, задача имеет два решения, если эти интервалы равны – одно решение, если же интервал прямой меньше интервала плоскости, задача не имеет решения, т.к. в этом случае прямая не лежит в плоскости, а пересекается с ней в заданной точке.

135
** Так как из любой точки, лежащей вне окружности (при lпл < lпр), можно провести к этой окружности две касательные, то задача в данном случае имеет два решения, при lпл = lпр – одно и при lпл > lпр – не имеет решения.
2.Если прямая параллельна плоскости, то, как известно, в этой плоскости имеется бесчисленное множество прямых, параллельных данной прямой. Чтобы через заданную точку, не лежащую в данной плоскости, провести прямую, параллельную данной плоскости, нужно вначале провести любую прямую в этой плоскости, а затем параллельно ей – искомую прямую*.
3.В случае, если прямая пересекается с плоскостью, нужно уметь находить проекцию точки их пересечения. Эта задача, как и в других видах проекций, решается в три приема: 1) через заданную прямую проводят вспомогательную плоскость, 2) строят прямую пересечения заданной и вспомогательной плоскостей и 3) находят точку, в которой заданная прямая пересекает построенную линию пересечения заданной и вспомогательной плоскостей. В проекциях с числовыми отметками в отличие от других видов проекций в качестве вспомогательной целесообразно применять плоскость, не проецирующую, а общего положения**. Эту вспомо-
гательную плоскость удобно задавать двумя горизонталями, проходящими через точки заданной прямой, имеющие целые отметки.
ПРИМЕР 78. Плоскость задана масштабом уклона i, прямая – ее проекцией А7В10. Найти проекцию точки К их встречи (рис. 170).
|
Решение. Через прямую АВ |
|
|
|
|
||
проведем |
вспомогательную плос- |
|
|
B10 |
|
||
кость, которую зададим горизонта- |
|
|
|
|
|||
лями, проходящими через точки А7 и |
|
|
|
|
|||
В10. Эти |
горизонтали параллельны |
|
|
N10 |
|
||
между собой, но направление их мо- |
|
|
|
||||
|
|
|
|
||||
жет быть взято произвольным. Най- |
|
|
K |
|
|||
дем точки М7 и N10 – пересечения |
|
|
|
i |
|||
проекций горизонталей с одинако- |
M7 |
|
|
10 |
|||
выми отметками заданной и вспомо- |
|
8,6 |
9 |
||||
гательной плоскостей и М7N10 – про- |
|
|
|||||
|
|
|
|
||||
екцию линии пересечения этих плос- |
|
|
8 |
|
|||
|
|
|
|
|
|
|
|
костей. Искомая точка К = А7В10 |
|
A7 |
7 |
|
|||
M7N10. Отметку точки К находят по |
|
|
|||||
|
|
|
|||||
интерполяции (в данном случае К8,6). |
|
|
|
|
|||
|
|
|
|
|
|
Рис. 170 |
|
|
|
|
|
|
|
||
|
* См. § 51, п. 1, пример 74, рис. 166 и § 49, рис. 162а. |
|
|
|
|||
136
** Горизонтально проецирующая плоскость проецируется на в прямую, совпадающую с проекцией заданной прямой, вследствие чего нахождение искомой точки затрудняется: приходится указанную горизонтально проецирующую плоскость совмещать с и строить на ней дополнительную проекцию.
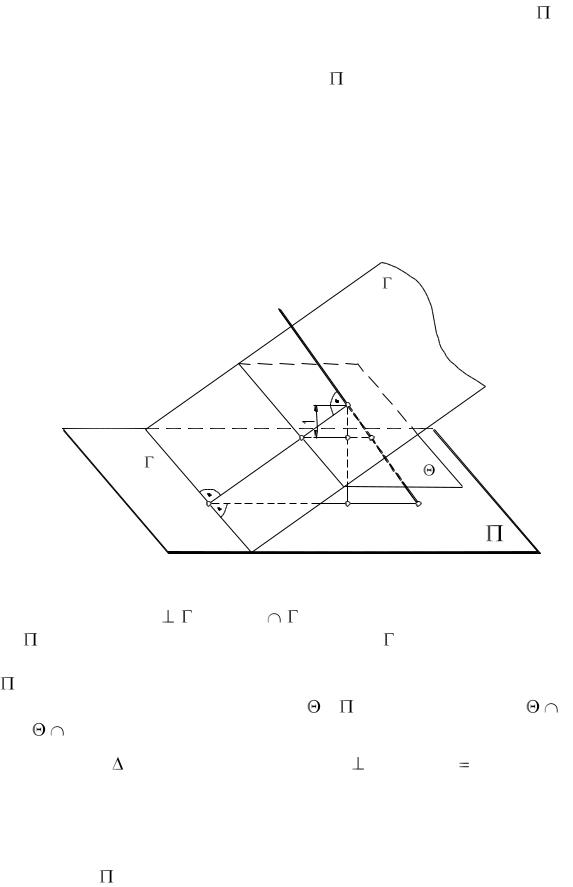
4. Известно, что прямая, перпендикулярная плоскости, перпендикулярна любой прямой этой плоскости, а следовательно, и линии ската.
Теорема. Если прямая перпендикулярна плоскости общего положения, то проекция прямой параллельна масштабу уклона данной плоскости, интервалы прямой и плоскости обратны по величине, а их числовые отметки возрастают в обратных направлениях.
m
C
' |
A |
F |
B |
|
|
|
|
|
|
|
m1 |
|
|
|
|
D |
E |
K |
|
|
Рис. 171 |
|
|
|
Если прямая m |
и С = m |
(рис. 171), то проекция m1, прямой m |
||
на совпадает с масштабом уклона плоскости или будет ему параллель- |
||||
на. Проведем через С линию ската CD. Опустим из С перпендикуляр СЕ на |
||||
и отложим на нем от точки С отрезок СF = 1 (единице в масштабе чер- |
||||
тежа). Через F проведем плоскость |
|
и найдем точки А = |
CD и |
|
В = |
m. Тогда интервал плоскости lпл = АF, а интервал прямой – lпр = |
||||||
= BF. Так как АВС – прямоугольный и СF АВ, то |
AF |
|
CF |
, откуда lпл = |
|||
|
|
||||||
|
|
|
CF |
|
BF |
||
= |
1 |
, т.е. интервалы прямой и плоскости взаимно обратны по величине. |
|||||
lпр |
|||||||
|
|
|
|
|
|
||
Из чертежа видно, что если на линии ската DC и прямой m от их точек пересечения с (точки D и К соответственно) нанести числовые отметки, то
