
UMLE6-106_F
.pdf
41
|
l2 |
|
l |
A2 |
|
M2 |
||
|
l1 


 M1 A1
M1 A1
а) |
б) |
Рис. 72
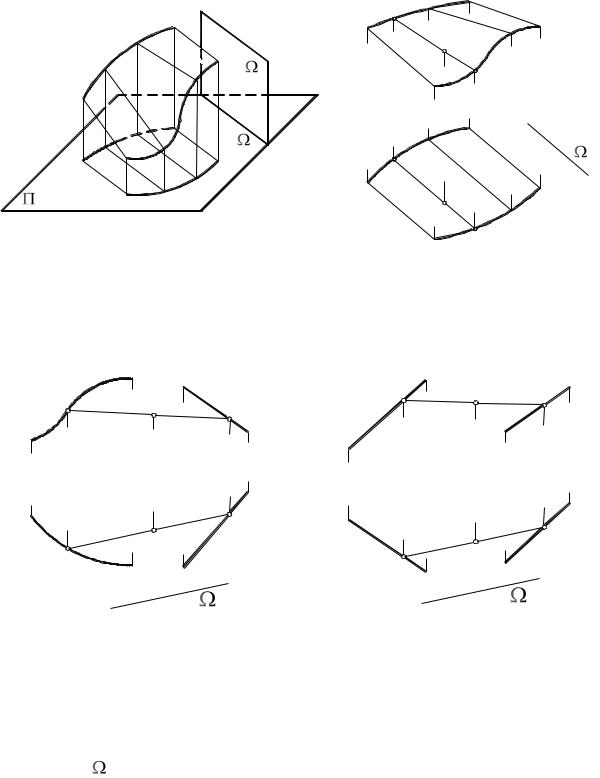
4. Поверхности с плоскостью параллелизма. Если прямая (обра-
зующая) движется по двум направляющим (l и m), оставаясь параллельной некоторой плоскости ( ), называемой плоскостью параллелизма, то получаемая линейчатая поверхность называется поверхностью с плоскостью параллелизма.
Направляющие l и m могут быть прямыми или кривыми (плоскими или пространственными). Плоскость параллелизма ( ) может иметь любое положение в пространстве.
В самом общем случае, когда обе направляющие (l и m) – кривые, поверхность с плоскостью параллелизма называется цилиндроидом (рис.
73).
Если одна направляющая (m) – кривая, а другая (l) – прямая, то по-
верхность называется коноидом (рис. 74).
Если обе направляющие (l и m) являются прямыми (скрещивающими-
ся), поверхность называется «косой плоскостью» или гиперболическим параболоидом (рис. 75). Последнее наименование связано с тем, что в сечениях этой поверхности различными плоскостями могут быть получены гиперболы или параболы в зависимости от положения секущих плоскостей. Определителем поверхности с плоскостью параллелизма является эта
плоскость и две направляющие. |
Для задания на эпюре любой поверх- |
ности с плоскостью параллелизма |
необходимы проекции направляющих |
l и m и положение этой плоскости, которая, в свою очередь, может быть задана любым способом. На рис. 73, 74 и 75 за плоскость параллелизма принята горизонтально проецирующая плоскость , заданная ее горизонтальным следом 1.
|
42 |
|
|
m2 |
|
|
A2 |
|
m |
M2 |
l2 |
|
|
|
B2 |
l |
m1 |
|
|
|
|
1 |
A1 |
|
|
m1 |
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
l1 |
|
|
M1 |
1 |
|
|
|
|
|
|
|
|
|
|
l1 |
|
|
|
|
|
B1 |
|
а) |
|
|
б) |
|
|
|
Рис. 73 |
|
|
|
l2 |
|
m2 |
|
|
A2 |
M2 |
|
A2 |
M2 |
|
||
|
B2 |
B2 |
||
|
|
|
||
m2 |
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
B1 |
m1 |
|
m1 |
|
|
||
M |
l1 |
B1 |
||
|
||||
|
1 |
|
M1 |
|
A1 |
l1 |
A |
||
|
|
1 |
|
|
|
|
1 |
1 |
|
|
|
|
||
|
Рис. 74 |
Рис. 75 |
|
Если известно, что некоторая точка М лежит на поверхности с плоскостью параллелизма, причем задана одна из ее проекций (например, М1), то для построения второй проекции (М2) нужно через заданную проекцию точки провести соответствующую (горизонтальную) проекцию образующей (А1В1 1). После этого следует найти точки А1 и В1 ее пересечения с проекциями направляющих l1 и m1 и построить вторую проекцию А2В2 образующей, а на ней найти искомую точку М2.
Оболочки, например, железобетонные, выполненные в виде поверхностей с плоскостью параллелизма, обладают хорошей прочностью. На практике они применяются для покрытия сооружений с большими проле-
|
|
|
|
|
43 |
|
|
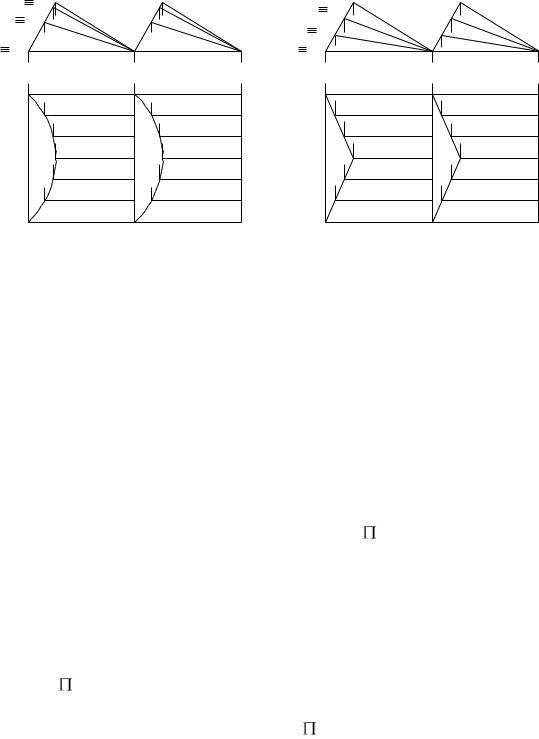
тами. Изготовление их удобно, так как опалубка может производиться по |
|||||||
прямым линиям. Покрытия промышленных зданий, выполненные в виде |
|||||||
ряда коноидов и гиперболических параболоидов, показаны на рис. 76а и б. |
|||||||
|
C |
|
D2 |
|
|
D2 |
|
|
C' |
C |
C' |
||||
|
B |
2 |
B' |
2 |
|||
|
|
|
B |
2 |
2 |
||
|
2 |
|
2 |
|
B' |
||
|
|
|
|
|
2 |
|
2 |
A |
A' |
|
|
A |
A' |
|
|
2 |
|
2 |
|
|
2 |
2 |
|
|
A' |
|
|
|
A' |
|
|
|
|
1 |
|
B' |
|
1 |
B' |
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
1 |
|
|
|
|
C' |
|
|
C' |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
D1 |
|
|
D1 |
|
|
|
|
C1 |
|
|
C1 |
|
|
|
|
B1 |
|
|
B1 |
|
|
A1 |
|
|
A1 |
||
|
|
|
|
а) |
|
|
б) |
|
|
|
|
|
Рис. 76 |
|
|
|
|
|
|
Б. Поверхности с криволинейной образующей |
|||
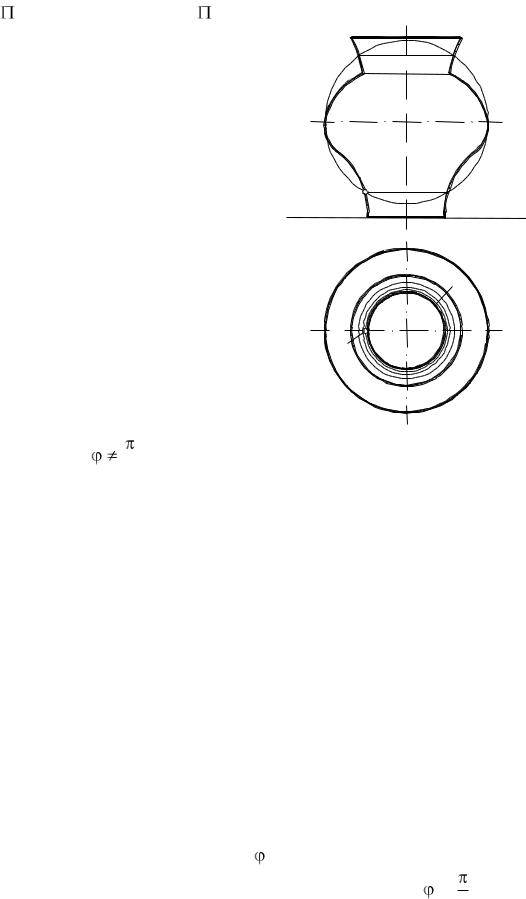
1. Поверхности вращения. Поверхностью вращения называется поверхность, образуемая некоторой линией, вращающейся вокруг неподвиж-
ной оси. В общем случае эта линия – кривая (рис. 77), а в частном – может быть прямой.
Определителем поверхности вращения является ось вращения i и образующая l. На рис. 77 показана поверхность, полученная вращением плоской кривой l вокруг оси i, перпендикулярной 1. Каждая точка М образующей l описывает при вращении окружность m с центром на оси i. Поэтому любая плоскость, перпендикулярная оси i, пересекает поверхность по окружности, называемой параллелью. Наименьшая из этих окружностей (k) называется горлом, а наибольшая (n) – экватором.
Кривые, получающиеся от сечения поверхности плоскостью, проходящей через ось i, называют меридианами. Если секущая плоскость параллельна 2, то меридиан называется главным. Если сфера с центром О на оси i поверхности вращения пересекается этой поверхностью, то линиями пересечения будут окружности. Если i 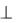 1, эти окружности проецируют-
1, эти окружности проецируют-
|
|
44 |
|
|
|
ся на |
1 в окружности, а на |
2 – в |
|
i2 |
|
отрезки, перпендикулярные проек- |
|
|
|||
|
|
|
|||
ции i2 оси. На рис. 77 сфера пересе- |
|
|
|
||
кает поверхность вращения по двум |
|
|
|
||
окружностям и касается по окружно- |
n2 |
|
O2 |
||
сти n. При вращении кривых второго |
|
||||
|
|
|
|||
порядка вокруг одной из осей их |
|
|
|
||
симметрии образуется поверхность |
|
|
m2 |
||
вращения также второго порядка: |
M2 |
|
|||
сфера, эллипсоид вращения, парабо- |
k2 |
|
|||
лоид вращения, однополостный и |
x |
|
|
||
двуполостный гиперболоиды враще- |
n1 |
|
|
||
ния. |
|
|
|
m1 |
|
При вращении прямой |
вокруг |
|
|
||
|
|
|
|||
неподвижной оси могут быть полу- |
|
i1 |
O1 |
||
чены различные кривые поверхности |
M1 |
k |
|
||
в зависимости от взаимного положе- |
|
||||
|
1 |
|
|||
|
|
|
|
|
|
ния образующей и оси вращения: а) |
|
|
|
||
конус вращения описывается пря- |
|
|
|
||
мой, |
пересекающейся с осью враще- |
|
|
|
|
ния под углом |
|
, б) цилиндр |
Рис. 77 |
2 |
вращения – прямой, параллельной оси вращения и в) однополостный гиперболоид вращения – прямой, скрещивающейся с осью вращения.
Эти линейчатые поверхности также имеют второй порядок. Прямая может пересечь поверхности второго порядка не более чем в двух точках. Линии пересечения указанных поверхностей плоскостями представляют собой различные кривые второго порядка в зависимости от положения се-
кущей плоскости. При пересечении различными плоскостями конуса вращения могут быть получены все кривые второго порядка: окружность, эллипс, парабола, гипербола и две пересекающиеся прямые, вследствие чего перечисленные кривые называют коническими сечениями.
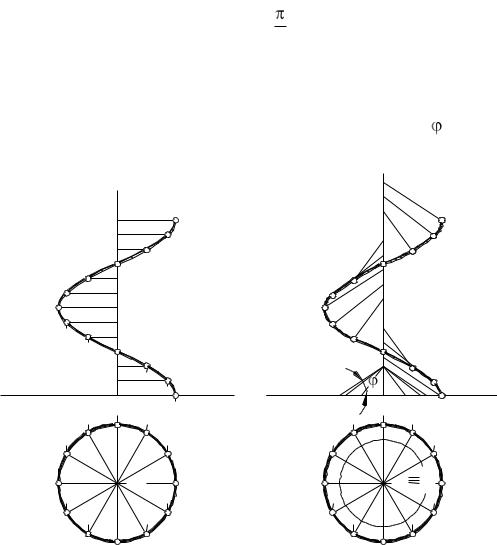
2. Винтовые поверхности. Если образующая (кривая или прямая)
равномерно вращается вокруг некоторой оси и одновременно равномерно перемещается вдоль этой оси, то поверхность, описанная образующей, называется винтовой. При прямолинейной образующей поверхность называется геликоидом. Геликоиды разделяются на открытые (если обра-
зующая и ось скрещиваются) и закрытые (если образующая и ось пересекаются).
В зависимости от величины угла , составляемого образующей с осью
вращения, различают два вида закрытых геликоидов: если = 2 , геликоид
45
называют прямым (рис. 78а), если  2 – косым или архимедовым (рис.
2 – косым или архимедовым (рис.
78б).
Для построения эпюра косого геликоида обычно используется так называемый направляющий конус, ось которого совпадает с осью винтовой поверхности, а образующие составляют с этой осью угол , равный углу наклона образующих геликоида.
a2 |
l2 |
a2 |
|
|
|
||
|
|
|
|
|
|
l2 |
|
|
m |
S2 |
m2 |
|
2 |
|
|
x |
|
x |
|
|
l1 |
l1 |
|
|
a1 |
S1 |
|
|
a1 |
||
|
m1 |
|
|
|
|
|
m1 |
а) |
|
б) |
|
Рис. 78
Прямой геликоид может также рассматриваться как коноид, направляющими которого являются винтовая линия и ее ось, а плоскость параллелизма перпендикулярна этой оси. Кромки ступеней обычной винтовой лестницы являются образующими такого геликоида.
3. Поверхности переноса. Если плоская кривая совершает в пространстве поступательное перемещение, скользя одной своей точкой по заданной направляющей, то поверхность, образованная такой кривой, на-
зывается поверхностью переноса.
Любая цилиндрическая поверхность может быть образована поступательным движением (переносом) криволинейной образующей по прямолинейной направляющей. В частности, цилиндр вращения может быть образован переносом окружности по прямой, перпендикулярной ее плоскости.
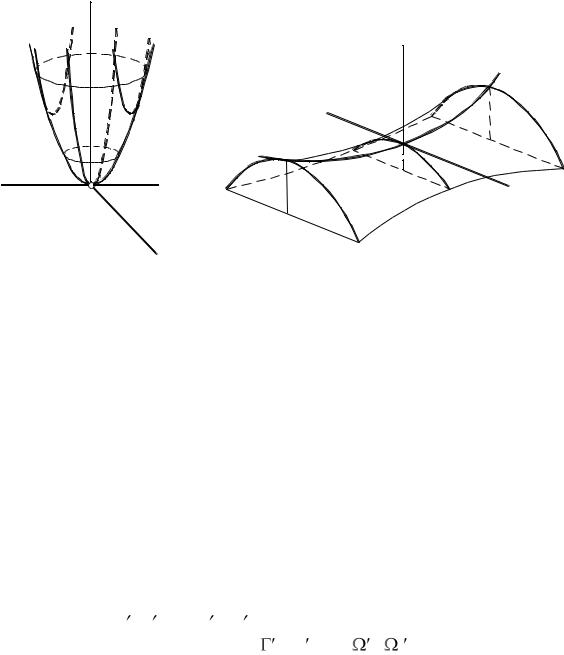
Если парабола (l), оставаясь себе параллельной, будет перемещаться, скользя вершиной по другой неподвижной параболе (m), лежащей в перпендикулярной плоскости, то поверхность, описанная первой параболой,
46
называется параболоидом. В том случае, когда оси обеих парабол направлены в одну сторону, параболоид называется эллиптическим (рис. 79а). Если оси обеих парабол направлены в противоположные стороны, параболоид называется гиперболическим (рис. 79б). Обе разновидности параболоида получены в данном случае как поверхности переноса, но гиперболический параболоид является в то же время линейчатой поверхностью (рис.
75).
|
z |
|
m |
|
z |
|
l |
|
|
|
m |
x |
|
y |
O |
l |
|
|
|
y |
|
а) |
б) |
Рис. 79
4. Каналовые поверхности. Каналовыми (или трубчатыми) назы-
ваются поверхности, образуемые движением окружности (или ее дуги) постоянного радиуса, центр которой перемещается по заданной кривой, а плоскость окружности совпадает с нормальной плоскостью к этой кри-
вой. Примером каналовой поверхности могут служить водопроводные или газовые трубы как прямые, так и изогнутые.
В. Понятие о каркасе поверхностей
В практике встречаются поверхности, закон образования которых не может быть выражен математически (поверхность фюзеляжа и крыльев самолета, корпуса корабля, кузова автомобиля, рельеф местности и др.).
Эти поверхности могут задаваться лежащими на них линиями. Чаще всего такими линиями (l , l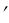 , …, m , m
, …, m , m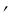 , …) являются сечения данной поверхности параллельными плоскостями ( ,
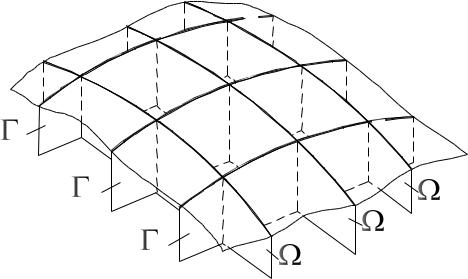
, …) являются сечения данной поверхности параллельными плоскостями ( , 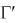 , …, ,
, …, , 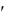 , …), показанные на рис. 80. Совокупность этих линий называют каркасом рассматриваемой
, …), показанные на рис. 80. Совокупность этих линий называют каркасом рассматриваемой
|
47 |
|
|
l' |
|
|
|
l'' |
|
|
l''' |
' |
|
m''' |
|
|
|
|
|
m'' |
'' |
m' |
''' |
|
||
|
''' |
'' |
|
' |
|
|
|
Рис. 80
поверхности. Поверхность, заданная каркасом, не вполне определена, так как могут существовать различные поверхности с тем же каркасом. Поэтому каркас определяет поверхность только приближенно.

48
Г Л А В А IV
ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ПЛОСКОСТЬЮ
ИПРЯМОЙ ЛИНИЕЙ
§22. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
Линия, получаемая при пересечении поверхности плоскостью, может быть плоской кривой или ломаной в зависимости от вида поверхности (кривая или гранная) и положения секущей плоскости*.
Чтобы построить проекции этой линии на чертеже, находят проекции ее отдельных точек и соединяют их соответствующим образом.
Среди точек линии пересечения имеются такие точки, которые выделяются своим расположением по отношению к плоскостям проекций или занимают особые места на линии сечения. Например, самая близкая и самая удаленная точка относительно той или иной плоскости проекций; точки, являющиеся границами видимой части линии, лежащие на очерке поверхности, и др. Эти точки называются опорными. Для определения опорных точек часто пользуются различными специальными приемами построения. Остальные точки линии пересечения называют случайными или произвольными и находят их обычно с помощью какого-либо одного метода, избранного для решения рассматриваемой задачи.
Существует несколько методов построения линии пересечения по-

49
* Линия сечения плоскостью гранной поверхности всегда получается ломаная, а линия сечения кривой поверхности – либо ломаная, либо кривая.
верхности с плоскостью. Один из них заключается в том, что берут не-
сколько вспомогательных плоскостей, которыми пересекают и поверх-
ность, и заданную плоскость. Каждая вспомогательная плоскость пересекает поверхность по кривой или ломаной, а заданную плоскость – по прямой; эти линии обязательно пересекутся между собой. Точки их пересечения и будут принадлежать искомой линии сечения. При практическом применении общего приема построения линии пересечения вспомогательные плоскости следует выбирать так, чтобы в сечении их с поверхностью получались наиболее простые линии – окружности или многоугольники. К тому же желательно, чтобы эти сечения на одну из плоскостей проекций проецировались в отрезок прямой.
Если сечения вспомогательными плоскостями получаются в виде окружности, то весьма важно, чтобы на одну из плоскостей проекций они проецировались в натуральную величину.
Указанный прием построения линии пересечения поверхности с плос-
костью называется способом вспомогательных плоскостей.
А. Пересечение плоскостью поверхности вращения
Способ вспомогательных плоскостей удобен для построения линии пересечения плоскостью поверхности вращения.
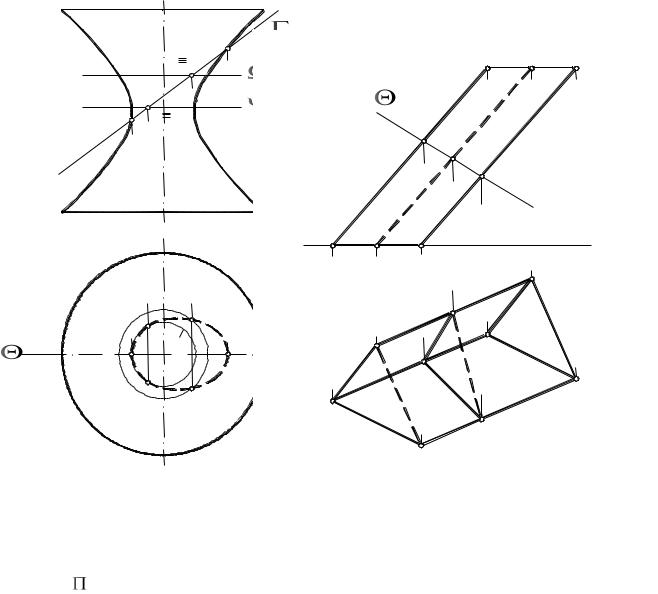
ПРИМЕР 25. Построить линию пересечения однополосного гипербо-
лоида вращения с фронтально проецирующей плоскостью |
(рис. 81). |
||||
Решение. Первую вспомогательную плоскость |
проводим через ось i |
||||
гиперболоида параллельно |
2. Она пересечет гиперболоид по главному |
||||
меридиану, дающему очерк поверхности на плоскость |
2, а плоскость – |
||||
по прямой, фронтальная проекция которой совпадает с |
2. Точки 1 и 2 пе- |
||||
ресечения главного меридиана с заданной плоскостью |
|
принадлежат ис- |
|||
комой линии пересечения. Фронтальные проекции 12 |
и 22 |
этих точек вид- |
|||
ны на рисунке, а горизонтальные проекции 11 |
и 21 следует найти с помо- |
||||
щью линий связи на горизонтальном следе |
1 плоскости . Остальные |
||||
вспомогательные плоскости ( |
и ) целесообразно провести параллельно |
||||
1. Плоскость проводим через горловое сечение. Эта плоскость пересекает гиперболоид по окружности k, а плоскость – по прямой 34. Фронтальные проекции 32 и 42 точек 3 и 4 сливаются в одну точку и видны на
рисунке, а горизонтальные проекции 31 |
и 41 находим построением на гори- |
зонтальной проекции k1 окружности k. |
Плоскость пересечет гиперболо- |
ид по окружности l, а плоскость – по прямой 56. Фронтальные проекции 52 и 62 точек 5 и 6 сливаются в одну точку и видны на рисунке, а горизон-
50
тальные их проекции находим на проекции l1 окружности l. Соединив последовательно точки 11, 31, 51, 21, 61, 41, 11, найдем горизонтальную проек-
|
|
|
i2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
52 |
2 |
22 |
|
A' |
B' |
C' |
|
|
|
|
|
2 |
2 |
2 |
||
|
l2 |
|
|
6 |
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
k2 |
|
|
2 |
|
|
|
12 |
32 |
4 |
|
2 |
|
|
|
||
|
|
|
|
|
|||||
2 |
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
A |
B |
C |
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
B' |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
61 |
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 |
k |
|
|
B |
A' |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
2 |
11 |
|
|
|
21 |
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
31 |
|
|
|
|
1 |
|
|
l1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
51 |
|
|
|
|
C' |
|
|
|
|
|
A |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
1 |
|
|
Рис. 81 Рис. 82
цию искомой линии сечения. Если считать, что поверхность гиперболоида ограничена верхним основанием (отсеком плоскости в виде круга, параллельного 1), то горизонтальная проекция линии сечения будет невидимой
– закрываться этим основанием. Фронтальной проекцией линии сечения является отрезок 1222.
Б. Пересечение плоскостью линейчатой поверхности
Для построения линии пересечения линейчатой поверхности плоскостью находят точки пересечения образующих поверхности с секущей плоскостью, которые соединяют надлежащим образом.
При пересечении поверхности проецирующей плоскостью одна из проекций линии сечения проецируется на соответствующий след этой
