
UMLE6-106_F
.pdf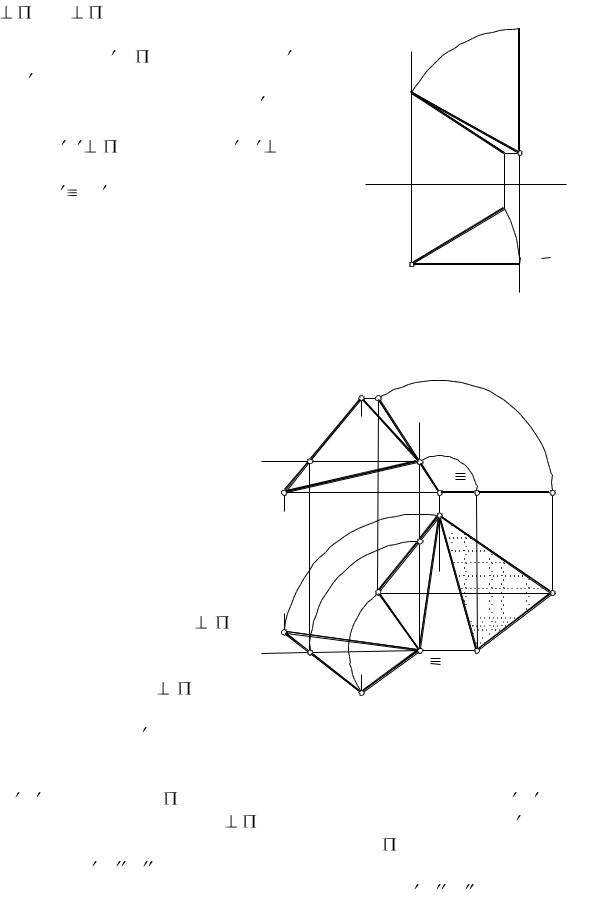
|
|
|
|
|
|
|
31 |
|
|
|
|
|
|
|
|
i |
1 и g |
2. Первую ось проведем через |
|
|
|
|
|
A' |
|
||||||
точку А и повернем АВ вокруг этой оси до |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|||||||||
положения АВ |
|
2, |
при этом А1В1 |
х, а |
|
i |
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2В2 |
выражает натуральную величину |
АВ. |
|
A2 |
|
|
|
|
|||||||
Вторую ось g проведем через В и повер- |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||
нем вокруг нее заданную прямую до поло- |
|
|
|
|
|
|
|
||||||||
жения А В |
|
1, при этом А2 В2 |
х, а го- |
|
|
|
|
B |
B' |
|
|||||
|
|
|
|
|
g2 |
|
|||||||||
ризонтальная проекция прямой сольется в |
|
|
|
|
2 |
2 |
|
||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||
точку А1 |
В1 . |
|
|
|
|
|
|
x |
|
|
|
B1 |
|
|
|
|
ПРИМЕР 18. Определить натураль- |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
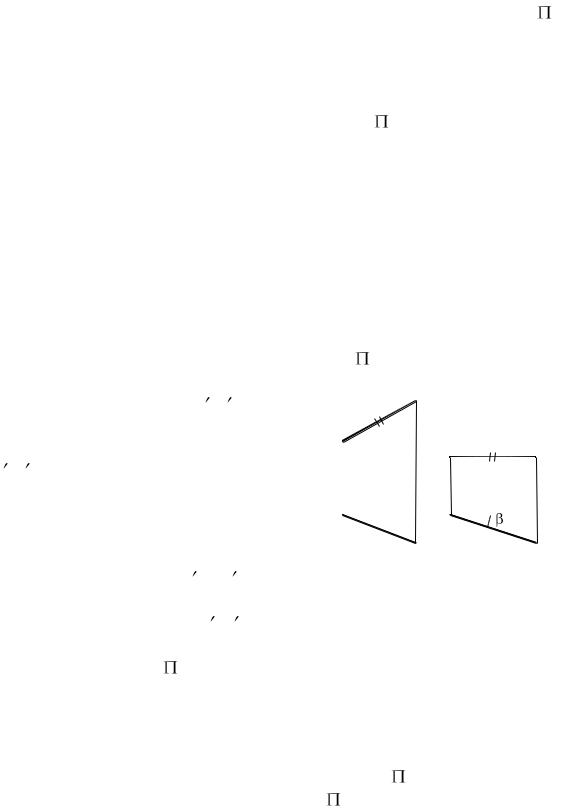
ную величину треугольника АВС (рис. 61). |
|
|
|
|
|
|
|
||||||||
|
Решение. Эта задача решается так- |
|
A1 |
|
|
B'=A' |
|||||||||
же в два приема: вначале заданную пло- |
|
|
i1 |
|
|
1 |
1 |
||||||||
|
|
|
g1 |
|
|
||||||||||
скую фигуру поворачивают вокруг оси, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
перпендикулярной одной |
плоскости про- |
|
|
|
|
|
|
|
|||||||
екций до положения, перпендикулярного |
|
|
Рис. 60 |
|
|
||||||||||
второй плоскости, |
после чего |
|
|
B B' |
|
|
|
|
|
||||||
вращением вокруг оси, пер- |
|
|
|
|
|
|
|
||||||||
|
|
2 |
2 |
|
|
|
|
|
|||||||
пендикулярной второй плос- |
|
|
|
|
|
|
|
|
|
||||||
кости, поворачивают до по- |
D2 |
|
|
|
i 2 |
|
|
|
|||||||
ложения, параллельного пер- |
|
|
|
|
|
|
|
|
|||||||
вой плоскости. |
На эту плос- |
|
|
|
C |
A' |
g |
|
|
||||||
кость фигура спроецируется в |
A2 |
|
|
|
2 |
2 |
2 |
|
B'' |
||||||
|
|
|
|
A' |
C'' |
|
|||||||||
натуральную величину. Вос- |
|
|
|
|
|
2 |
|
2 |
|||||||
|
|
|
D' |
1 |
|
|
|
||||||||
пользовавшись |
соображения- |
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
|||||||
ми, приведенными в примере |
|
|
|
|
|
|
|
|
|
||||||
14 (§ 18), построим в плоско- |
|
|
B' |
|
|
g1 |
|
|
B'' |
||||||
сти АВС горизонталь СD. |
|
|
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|||||||
Первую ось вращения i |
1 |
A1 |
|
|
|
|
|
|
|
|
|||||
проведем |
через вершину |
С. |
|
|
|
|
|
|
C'' |
|
|
||||
Вокруг оси i повернем фигуру |
D1 |
|
|
C1 |
i1 |
|
|
||||||||
|
|
1 |
|
|
|||||||||||
до положения АВС |
2, |
при |
|
|
B1 |
|
|
|
|
|
|
||||
этом горизонтальная проекция |
|
|
|
|
|
|
|
|
|||||||
горизонтали С1D1 |
будет па- |
|
|
|
|
|
|
|
|
|
|||||
раллельна линиям связи, а |
|
|
|
Рис. 61 |
|
|
|
||||||||
взаимное расположение горизонтальных проекций вершин сохранится |
|||||||||||||||
(А1 В1 С1 = А1В1С1). На |
2 треугольник спроецируется в прямую А2 В2 . |
|
|||||||||||||
|
Вторую ось вращения g |
2 проведем через вершину А |
и повер- |
||||||||||||
нем треугольник до положения, параллельного |
1, при этом фронтальная |
||||||||||||||
проекция А2 С2 |
В2 |
будет перпендикулярна линиям связи, а горизонталь- |
|||||||||||||
ная – выразит истинную величину треугольника (А1 В1 |
С1 |
= АВС). |
|
||||||||||||
32
Б. Плоскопараллельное перемещение
Плоскопараллельным называется такое перемещение фигуры в пространстве, при котором все ее точки движутся в плоскостях, параллель-
ных между собой. В плоскопараллельном движении относительно 1 все точки фигуры перемещаются в горизонтальных плоскостях, и горизонтальные проекции этих точек перемещаются, не изменяя своего взаимного положения. Фронтальные проекции тех же точек переходят в новые положения, двигаясь по прямым, перпендикулярным линиям связи. При плоскопараллельном движении относительно 2 происходят аналогичные перемещения проекций. Плоскопараллельное перемещение может рассматриваться как вращение вокруг некоторой оси, перпендикулярной плоскости проекций и не показанной на чертеже.
Метод вращения вокруг проецирующих прямых, как было показано, очень прост, нагляден и удобен в построениях, но при решении задач со сложными фигурами иногда новые проекции частично налагаются на старые и затемняют чертеж. Поэтому в ряде случаев более целесообразен метод плоскопараллельного перемещения, позволяющий строить новые проекции фигуры в любом свободном месте чертежа.
ПРИМЕР 19. Преобразовать прямую АВ общего положения в го-
ризонталь и определить угол ее наклона к |
2 (рис. 62). |
|
|
||||||||
Решение. |
Расположим |
новую |
|
|
|
|
B2 |
|
|
||
фронтальную проекцию А2 В2 |
прямой |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
в любом месте эпюра перпендикуляр- |
A2 |
|
|
|
|
|
|
|
|||
но линиям связи, соблюдая условие |
|
|
|
A' |
|
B'2 |
|||||
|
|
||||||||||
|
|
|
2 |
|
|||||||
А2 В2 = А2В2. Через заданные гори- |
|
|
|
|
|
|
|
|
|||
зонтальные проекции А1 |
и В1 |
точек А |
|
|
|
|
|
|
|
|
|
и В проведем |
прямые, |
перпендику- |
|
|
|
|
|
|
|
|
|
A1 |
|
A' |
|
|
|||||||
лярные линиям связи, и найдем точки |
|
|
|
||||||||
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
B' |
их пересечения с линиями связи, про- |
|
|
|
B1 |
|
||||||
|
|
|
1 |
||||||||
веденными через точки А2 |
и В2 . Новой |
|
|
|
|
|
|
|
|
||
горизонтальной проекцией отрезка АВ |
|
|
|
Рис. 62 |
|
|
|||||
будет являться отрезок А1 В1 , равный натуральной величине отрезка АВ, а угол 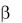 выразит истинную величину угла наклона заданной прямой к плоскости 2.
выразит истинную величину угла наклона заданной прямой к плоскости 2.
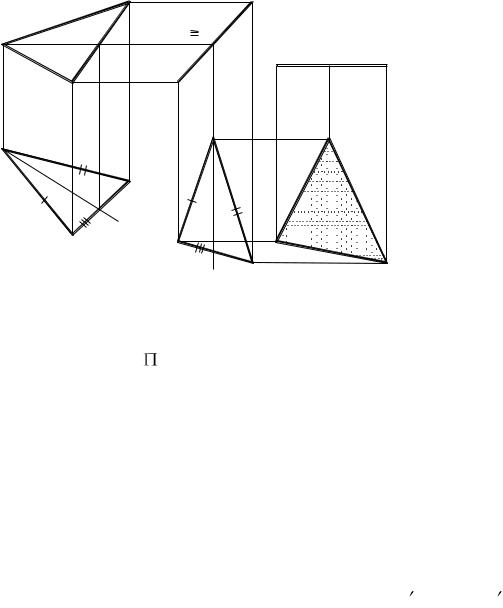
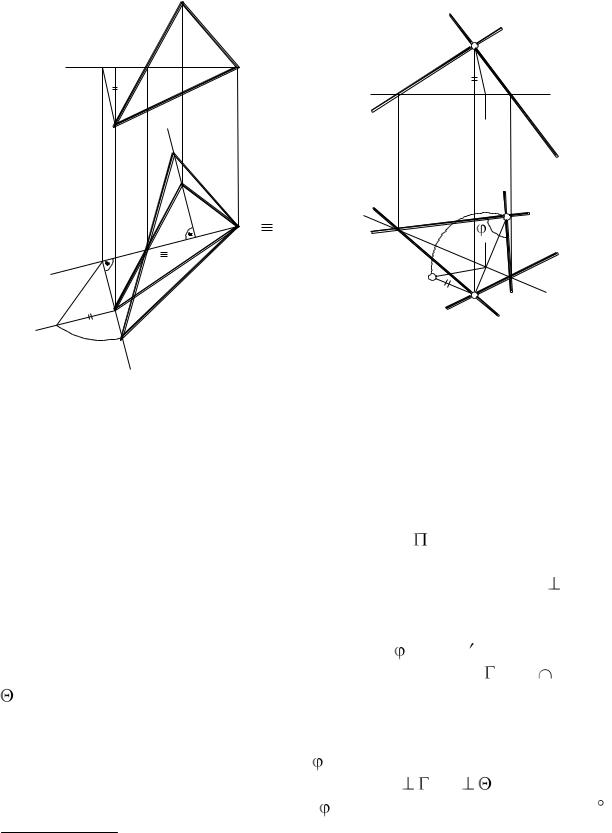
ПРИМЕР 20. Определить натуральную величину треугольника АВС
(рис. 63).
Решение. Как и в примере 18, задача должна решаться в два приема: вначале треугольник размещают в положение, перпендикулярное одной из плоскостей проекций (например, 2), после чего – в положение, параллельное другой плоскости ( 1). Для выполнения этих пре-
|
|
|
|
33 |
|
|
|
|
|
|
C2 |
|
C' |
|
|
|
|
|
|
|
2 |
|
|
h |
2 |
|
A' |
h' |
|
|
|
A2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
B'' |
A'' |
C'' |
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
2 |
B2 |
|
|
B' |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
A' |
|
A'' |
|
|
|
|
|
1 |
|
1 |
|
A1 |
|
|
|
|
|
|
|
|
h |
1 |
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h'1 |
B'' |
|
|
B1 |
|
|
B' |
|
1 |
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
C' |
|
C'' |
|
|
|
|
|
1 |
|
1 |
Рис. 63
образований, проведем проекции h2 и h1 горизонтали h плоскости АВС и построим в любом месте на 1 новую проекцию А1'В1'С1' = А1В1С1 так, чтобы h1' расположилась параллельно линиям связи. Для построения новой фронтальной проекции заданного треугольника проводим через точки А1', В1' и С1' линии связи, а через точки А2, В2 и С2 – прямые, перпендикулярные этим линиям. В пересечениях соответствующих линий находим точки А2', В2' и С2', являющиеся новыми фронтальными проекциями вершин заданного треугольника. Эти точки будут лежать на одной прямой. Затем переместим фронтальную проекцию В2'А2'С2', являющуюся отрезком прямой, в новое положение В2''А2''С2'' в любом месте чертежа, но перпендикулярно линиям связи. После этого через точки А1', В1' и С1' проведем прямые, перпендикулярные линиям связи, и найдем точки их пересечения с линиями связи, проведенными, через точки А2 , В2
, В2 и С2
и С2 . Полученный треугольник А1''В1''С1'' является новой горизонтальной проекцией заданного треугольника АВС и выражает его натуральную величину.
. Полученный треугольник А1''В1''С1'' является новой горизонтальной проекцией заданного треугольника АВС и выражает его натуральную величину.
В. Вращение вокруг линий уровня
Метод вращения вокруг линий уровня дает возможность плоскость общего положения одним вращением совместить с плоскостью уровня и,
следовательно, сразу получить истинную величину плоской фигуры, лежащей в заданной плоскости. Этот метод, кроме того, удобен для определения углов между двумя пересекающимися прямыми, двумя плоскостями, прямой и плоскостью.
Рассмотрим вначале вращение точки вокруг линии уровня (например,
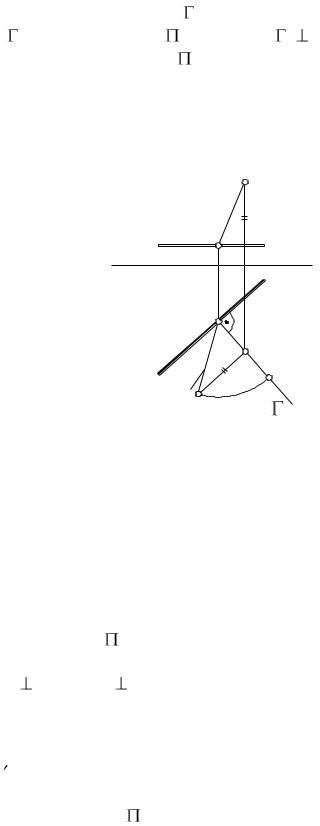
34
вокруг горизонтали) до совмещения с плоскостью уровня. Пусть даны проекции А1 и А2 точки А и h1 и h2 – горизонтали h (рис. 64). Точка А, вращаясь вокруг горизонтали h, описывает окружность радиуса r, распо-
ложенную в горизонтально проецирующей плоскости |
, |
перпендикуляр- |
ной этой горизонтали. Плоскость проецируется на |
1 в прямую 1 h1, |
|
а окружность – в отрезок той же прямой. На плоскость |
2 |
эта окружность |
проецируется в эллипс (на рисунке не показан). Следовательно, при вращении точки вокруг горизонтали ее горизонтальная проекция движется по перпендикуляру к горизонтальной проекции горизонтали, а ее фронтальная проекция описывает эллипс.
Радиусом r указанной окружности яв- |
|
|
A2 |
|||
ляется перпендикуляр, опущенный из |
|
r2 |
|
|||
точки А на горизонталь, а центром – точка |
|
|
||||
О, основание этого перпендикуляра. После |
h2 O2 |
|
||||
совмещения точки А с плоскостью уровня, |
|
|
|
|||
проведенной через горизонталь h, эта точ- |
x |
|
|
|||
ка займет положение А' на расстоянии |
|
O1 |
|
|||
радиуса r = ОА = ОА' от центра О. Та- |
|
|
||||
ким образом, для построения горизонталь- |
h1 |
r1 |
A1 |
|||
ной проекции А1' точки А' достаточно опре- |
||||||
OA |
A' |
|||||
делить истинную величину радиуса r = |
|
1 |
||||
|
|
|||||
= ОА и отложить ее от точки О1 на про- |
|
. |
|
|||
|
в |
|
||||
должении проекции О1А1. На рис. 64 эта |
|
. |
1 |
|||
|
н |
|
||||
величина |
определена методом |
прямо- |
|
|
|
|
угольного |
треугольника. Отрезок |
О1А1' |
|
Рис. 64 |
|
|
выражает истинную величину расстояния точки А до горизонтали h. Аналогичные построения можно выполнить при вращении точки вокруг фронтали.
ПРИМЕР 21. Дан треугольник АВС (рис. 65), определить его истинную величину.
Решение. В плоскости треугольника проведем (желательно через одну из вершин) линию уровня (например, горизонталь h) и повернем вокруг нее треугольник до положения А'В'С' 1. Проекции точек С и D, лежащих на оси вращения h, останутся на месте, а проекции вершин А и В переместятся по прямым О1A1 h1 и В1В1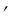 h1. Чтобы найти новые положения А1' и В1' этих проекций, нужно для одной из указанных точек (например, А) выполнить построения, приведенные на рис. 64. Через полученную точку А1' и точку D1' проведем прямую до пересечения в точке В1' с продолжением прямой В1В1 . Соединив точки А1', В1' и С1', получим новую горизонтальную проекцию треугольника, выражающую его натуральную величину. Проекция треугольника на 2 обратится в отрезок прямой, совпадающий с h2. Так как эта проекция не нужна для реше-
h1. Чтобы найти новые положения А1' и В1' этих проекций, нужно для одной из указанных точек (например, А) выполнить построения, приведенные на рис. 64. Через полученную точку А1' и точку D1' проведем прямую до пересечения в точке В1' с продолжением прямой В1В1 . Соединив точки А1', В1' и С1', получим новую горизонтальную проекцию треугольника, выражающую его натуральную величину. Проекция треугольника на 2 обратится в отрезок прямой, совпадающий с h2. Так как эта проекция не нужна для реше-
|
|
|
|
|
35 |
|
|
|
|
|
|
|
|
|
|
B2 |
|
|
|
|
K2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
O2 |
D2 |
|
C2 |
|
|
A2 |
|
|
|
B2 |
|
|
|
|
|
|
h2 |
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
a |
|
|
O2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
|
b |
|
|
|
B' |
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
a |
|
|
b' |
K' |
|
|
|
|
|
|
1 |
|
|
1 |
|
||
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
C |
C' |
a' |
|
h1 |
|
|
|
|
O1 |
|
|
1 |
1 |
A |
|
|
|||
h1 |
|
D |
D' |
|
1 |
|
|
||||
|
|
1 |
1 |
|
|
1 |
R |
O |
b1 |
||
|
|
|
|
|
|
|
|
|
1 |
||
|
|
|
|
|
|
|
K0 |
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
K1 |
|
1 |
A |
|
A' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
1 |
|
|
|
|
|
|
|
|
|
Рис. 65 Рис. 66
ния данной задачи, она на рис. 65 не показана.
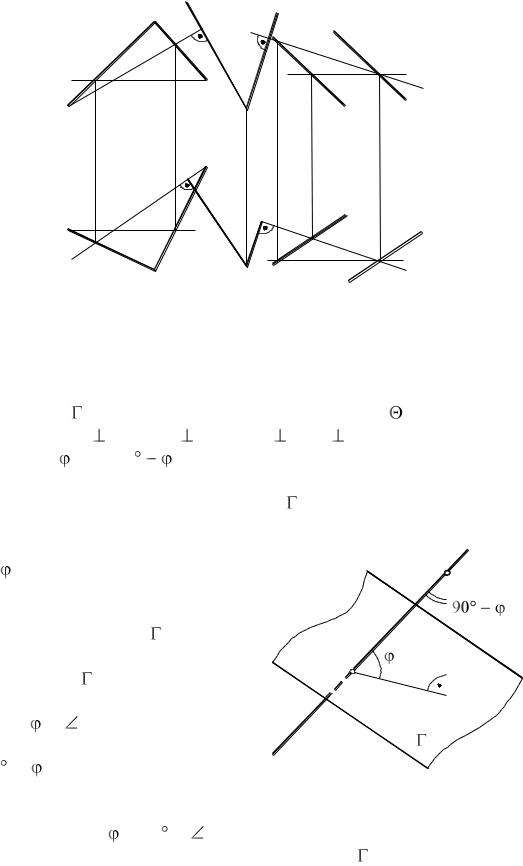
ПРИМЕР 22. Две прямые а и b общего положения пересекаются в точке К (рис. 66). Определить угол между ними.
Решение. В плоскости, проходящей через заданные прямые, проводим горизонталь h. Она пересечет прямые а и b в точках А и В. Повернем заданный угол вокруг горизонтали до положения АВК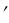 1. При этом вращении точки А и В остаются неподвижными, а точка К описывает окружность. Горизонтальная проекция точки К будет перемещаться по прямой О1К1 А1В1. Чтобы найти новую горизонтальную проекцию К1' точки К, определим натуральную величину радиуса вращения ОК (см. рис. 64) и отложим ее на продолжении отрезка О1К1*. Искомый угол = А1K1 В1.
1. При этом вращении точки А и В остаются неподвижными, а точка К описывает окружность. Горизонтальная проекция точки К будет перемещаться по прямой О1К1 А1В1. Чтобы найти новую горизонтальную проекцию К1' точки К, определим натуральную величину радиуса вращения ОК (см. рис. 64) и отложим ее на продолжении отрезка О1К1*. Искомый угол = А1K1 В1.
ПРИМЕР 23. Даны две пересекающиеся плоскости: (АВ ВС) и (d e). Определить двугранный угол между этими плоскостями
(рис. 67).
Решение. Двугранный угол между двумя плоскостями, как извест-
но, измеряется его линейным углом |
. Из произвольной точки К опус- |
||
тим на заданные плоскости перпендикуляры: m |
и n |
. Плоский угол |
|
между ними будет равен искомому углу |
либо дополняющему его до 180 |
||
* На рис. 66 отрезок О1К1' отложен в строну, противоположную О1К1, чтобы не затемнять чертеж.
|
36 |
|
|
|
|
B |
m2 |
n |
|
|
|
2 |
F |
2 |
|
|
|
|
f2 |
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
h2 |
2 |
|
|
|
|
|
A2 |
C2 |
|
|
|
e2 |
|
K |
|
d2 |
||
|
|
2 |
|
|
|
|
C1 |
|
|
|
|
|
m1 |
n |
h |
d1 |
e |
A1 |
F |
1 |
|
||
|
1 |
|
1 |
||
|
|
|
|
||
H1 |
1 |
|
|
|
|
K1 |
|
f1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
B1 |
|
|
|
|
|
Рис. 67
(как углы с взаимно перпендикулярными сторонами). Для построения указанных перпендикуляров в каждой из заданных плоскостей проведем горизонталь
и фронталь (в пл. |
– горизонталь СН, фронталь AF, в пл. – горизонталь h, |
||||||||
фронталь f), тогда m1 |
С1Н1, |
m2 |
A2F2 и n1 |
h1, n2 f2. Полученный угол ме- |
|||||
жду m и n равен |
или 180 |
. Определение натуральной величины этого уг- |
|||||||
ла может быть произведено так, как изложено в примере 22 (рис. 66). |
|||||||||
ПРИМЕР 24. Дана прямая m и плоскость |
. Определить угол между ними |
||||||||
(рис. 68). |
|
|
|
|
|
|
|
|
|
Решение. Искомым углом являет- |
|
|
|||||||
ся угол |
между данной прямой и ее |
|
K |
||||||
|
|||||||||
ортогональной проекцией на заданную |
|
||||||||
|
|
||||||||
плоскость. Из произвольной точки К |
|
|
|||||||
прямой m опустим на пл. |
перпенди- |
|
|
||||||
куляр КА. Предположим, что прямая m |
C |
|
|||||||
пересекается с пл. в точке С (положе- |
|
||||||||
|
|
||||||||
ние которой не определено), тогда ис- |
|
A |
|||||||
|
|||||||||
комый угол |
= |
АСК, а угол АКС ме- |
m |
||||||
жду прямой m и перпендикуляром АК |
|||||||||
|
|
||||||||
равен 90 |
– |
. Применяя метод враще- |
|
|
|||||
ния вокруг линии уровня, |
определим |
|
|
||||||
угол АКС (см. пример 22, рис. 66), по- |
Рис. 68 |
||||||||
сле чего найдем угол |
= 90 – |
АКС. Такое решение освобождает от не- |
|||||||
обходимости отыскания точек А и С пересечения пл. с прямыми m и КА.
37
Г Л А В А III
КРИВЫЕ ЛИНИИ И ПОВЕРХНОСТИ
§ 20. КРИВЫЕ ЛИНИИ
Кривую линию, или просто «кривую», можно определить как траекторию движения точки. Если все точки кривой лежат в одной плоскости, то такую кривую называют плоской. Любые две хорды плоской кривой либо пересекаются, либо параллельны между собой.
Пространственными кривыми (или «кривыми двоякой кривизны») на-
зывают такие линии, точки которых не лежат в одной плоскости. Две произвольные хорды пространственной кривой, проведенные через разные точки, как правило, скрещиваются.
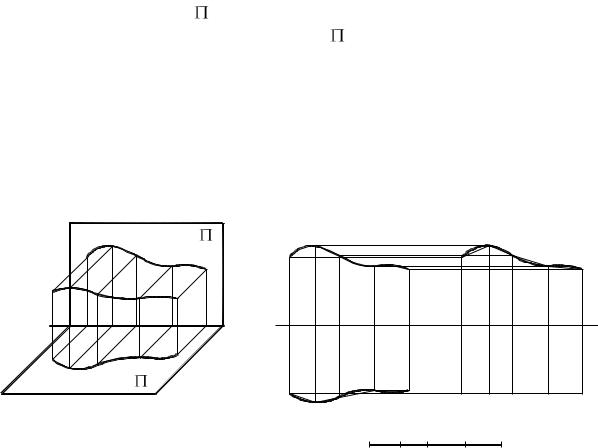
На рис. 69а показана дуга АЕ некоторой пространственной кривой и ее проекции.
Совокупность прямых АА1, ВВ1, СС1 …, проецирующих точки А, В, С … кривой на плоскость 1, образует кривую поверхность АА1В1С1 …, линия пересечения которой с плоскостью 1 представляет собою горизонтальную проекцию А1Е1 заданной дуги кривой. Следовательно, эта кривая поверхность является горизонтально проецирующей. Аналогично поверхность АА2В2С2 … – фронтально проецирующая. Обе эти проецирующие поверхности пересекаются между собой в пространстве по заданной кривой АВС …
В практике может возникнуть необходимость определения длины дуги отрезка кривой. Если кривая имеет двоякую кривизну, то для решения
|
|
B2 |
|
|
2 |
|
B |
|
|
|
|
B' |
|
|
|
|
A |
C |
|
A |
2 |
|
|
|
A' |
2 |
C' |
|
|
||
|
|
D |
|
|
|
|
|
|
D' |
|
|||||
|
2 |
|
2 |
E |
2 |
|
|
|
|
2 |
|
2 |
E' |
||
|
|
|
|
2 |
|
C2 |
|
|
|
|
|
|
2 |
||
|
|
|
|
|
2 |
|
D2 |
E |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
A |
B |
C |
D |
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
A1 |
B1 |
C1 |
D1 |
E1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1 |
E1 |
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
A |
|
C1 |
|
|
A' |
B' |
C' |
D' |
E' |
|
|
|
|
|
|
1 |
B1 |
|
|
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
A' |
B' |
C' |
D' |
|
E' |
|
|
|
|
а) |
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
Рис. 69 |
|
|
|
|
|
|
|
|
|

38
этой задачи производят два построения: 1) развертывают кривую на плоскость и 2) спрямляют ее.
Пусть требуется определить длину дуги кривой АЕ, показанной на рис. 69а. Так как эта кривая одновременно принадлежит и горизонтально проецирующей и фронтально проецирующей поверхностям, то для того, чтобы получить на эпюре истинную длину дуги кривой, нужно любую из проецирующих поверхностей развернуть в плоскость и расположить эту последнюю параллельно одной из плоскостей проекций. На рис. 69б горизонтально проецирующая поверхность развернута в горизонтально про-
ецирующую плоскость, параллельную плоскости 2 (след |
развернутой |
плоскости А1 Е1 х). На этом следе отложены длины хорд, |
стягивающих |
произвольные участки А1В1, В1С1 … горизонтальной проекции А1Е1 заданной дуги кривой (А1 В1 = А1В1, В1 С1
= А1В1, В1 С1 = В1С1 и т.д.). Построение фронтальных проекций А2 , В2 , С2
= В1С1 и т.д.). Построение фронтальных проекций А2 , В2 , С2 … точек кривой понятно из рисунка. Соединив эти проекции точек плавной кривой, получим приближенную развертку А2 Е2
… точек кривой понятно из рисунка. Соединив эти проекции точек плавной кривой, получим приближенную развертку А2 Е2 заданной дуги кривой. Длина развертки будет тем ближе к истинной длине заданной дуги, чем короче взяты дуги А1В1, В1С1 …
заданной дуги кривой. Длина развертки будет тем ближе к истинной длине заданной дуги, чем короче взяты дуги А1В1, В1С1 …
Полученную развертку принято спрямлять. Для этого ее дуги А2 В2 , В2 С2 … заменяют стягивающими их хордами, длины которых последовательно откладывают вдоль произвольной прямой l. Отрезок А Е
… заменяют стягивающими их хордами, длины которых последовательно откладывают вдоль произвольной прямой l. Отрезок А Е представляет собой спрямленную дугу АЕ заданной кривой.
представляет собой спрямленную дугу АЕ заданной кривой.
§ 21. ПОВЕРХНОСТИ
Поверхности в начертательной геометрии рассматриваются как сово-
купность последовательных положений линии, перемещающейся в про-
странстве. Такая линия называется образующей. Если образующая – прямая, то поверхность называется линейчатой.
При перемещении в пространстве кривой получается поверхность с кри-
волинейной образующей. Криволинейная образующая в процессе дви-
жения может менять свою форму.
Все поверхности разделяют на гранные и кривые. Гранная поверхность представляет собой совокупность нескольких пересекающихся отсеков плоскостей. Остальные поверхности являются кривыми.
Поверхность называется закономерной, если известны законы движения образующей и изменения формы последней. В случае отсутствия таких законов поверхность считается незакономерной.
Для задания поверхности на эпюре достаточно иметь проекции ее оп-
ределителя. Определителем поверхности называется совокупность эле-
39
ментов поверхности (ее параметров), выделяющих рассматриваемую поверхность из всего класса поверхностей.
Для придания большей наглядности изображения на эпюре часто строят проекции очерка поверхности, а также ее наиболее важные линии и точки. Очерком поверхности называют линию касания этой поверхности и обертывающей ее проецирующей поверхности.
А. Линейчатые поверхности
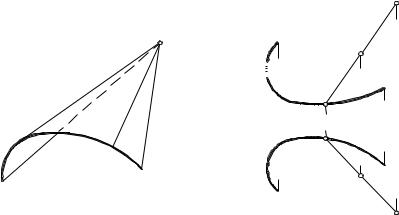
1. Коническая поверхность (или конус) – это поверхность (рис. 70),
образованная движением прямой (образующей), проходящей через неподвижную точку S (вершину) и скользящей по некоторой линии l (направ-
ляющей). Определителем конической поверхности является направляющая l и вершина S, проекциями которых задается эта поверхность на эпюре.
|
S2 |
S |
M2 |
|
l2 
A2
l |
l1 |
A |
|
|
1 |
|
|
M1 |
|
|
S1 |
а) |
|
б) |
Рис. 70
Кривая l может быть как плоской, так и пространственной кривой, замкнутой или разомкнутой. Если линия l будет не кривая, а ломаная, то коническая поверхность обращается в гранную (пирамидальную) поверхность. Если направляющей будет прямая, коническая поверхность вырождается в плоскость. Так как направляющая пересекает все образующие, то любая линия на поверхности, пересекающая все образующие, может быть принята за направляющую.
Известно, что точка лежит на поверхности, если она находится на образующей или какой-либо другой линии, принадлежащей этой поверхности. На рис. 70б дана горизонтальная проекция М1 точки М, лежащей на конической поверхности. Для нахождения второй проекции этой точки
40
проводим через точки S1 и М1 горизонтальную проекцию образующей, которая пересечет направляющую в точке А1. Через точки А2 и S2 проведем фронтальную проекцию той же образующей и на ней найдем искомую проекцию М2.
2. Цилиндрическая поверхность (рис. 71) образуется движением прямой (образующей) параллельно заданному направлению m и скользящей по кривой l (направляющей).
|
|
l2 |
|
m2 |
|
|
|
|
|
|
|
|
A2 |
|
|
m |
M2 |
|
|
|
|
|
|
|
l |
|
M1 |
|
|
|
|
|
|
|
|
|
l1 |
A1 |
m1 |
|
|
|
|
а) б)
Рис. 71
Определителем цилиндрической поверхности является направляющая l и заданное направление m. На эпюре эта поверхность задается проекциями l и m. Если направляющая ломаная, то поверхность будет гранной (призматической). Если в качестве направляющей взята прямая, цилиндрическая поверхность вырождается в плоскость.
На рис. 71б дана фронтальная проекция М2 точки М, лежащей на цилиндрической поверхности. Для нахождения второй проекции этой точки проводим на 2 через точку М2 фронтальную проекцию образующей М2А2m2. Точка А2 – фронтальная проекция точки пересечения образующей с направляющей. На плоскости 1 находим горизонтальную проекцию А1 той же точки и через нее проводим горизонтальную проекцию образующей параллельно m1. На этой проекции находим искомую проекцию М1.
3. Поверхность с ребром возврата (или торс) (рис. 72) образуется прямой, перемещающейся в пространстве так, что она все время касается некоторой пространственной кривой, называемой ребром возврата. На эпюре торс задается проекциями ребра возврата l, являющимся его определителем.
