
UMLE6-106_F
.pdf
71
кая приближенная развертка будет тем ближе к действительной, чем большее число граней имеет вписанная пирамида*.
2. Развертки поверхностей наклонной призмы и цилиндра. Чтобы по-
строить развертку призмы ABCDEF (рис. 98а), следует вначале построить развертку боковой поверхности. Для этого нужно определить натуральные величины боковых граней, которые являются параллелограммами. Определим натуральные величины боковых ребер АF, ВD, СЕ любым методом, например,
методом замены плоскостей проекций. |
|
Заменим 2 на 4 так, чтобы 4 АF. Новая ось проекций х14 |
А1F1. На |
4 боковые ребра призмы спроецируются в натуральную величину. Затем определим расстояния между ребрами. Проведем плоскость , перпендикулярную ребрам, при этом  4. Обозначим точки пересечения плоскости с ребрами призмы цифрами 1, 2, 3. Найдем натуральную величину треугольника 123 любым способом, например, вращением вокруг оси i
4. Обозначим точки пересечения плоскости с ребрами призмы цифрами 1, 2, 3. Найдем натуральную величину треугольника 123 любым способом, например, вращением вокруг оси i 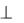 4, причем i
4, причем i 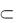 . Треугольник 11 21 31
. Треугольник 11 21 31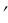 выражает натуральную величину сечения призмы плоскостью , а стороны этого треугольника равны расстояниям между ребрами.
выражает натуральную величину сечения призмы плоскостью , а стороны этого треугольника равны расстояниям между ребрами.
Для построения развертки (рис. 98б) проведем прямую l и отложим на ней отрезки, равные расстояниям между ребрами: 12 = 11 21 ; 23 = 21 31 и 31 = = 31 11 . Через точки 1, 2, 3, 1 проводим прямые, перпендикулярные линии l. На этих прямых отложим длины соответствующих ребер призмы: от точки 1 в одну сторону, вниз, – отрезок 1В = 14В4 и в другую сторону, вверх, – отрезок 1D = 14D4. Аналогично от точек 2 и 3 отложим отрезки 2А = 24А4 и 3С = 34С4 –
и 31 = = 31 11 . Через точки 1, 2, 3, 1 проводим прямые, перпендикулярные линии l. На этих прямых отложим длины соответствующих ребер призмы: от точки 1 в одну сторону, вниз, – отрезок 1В = 14В4 и в другую сторону, вверх, – отрезок 1D = 14D4. Аналогично от точек 2 и 3 отложим отрезки 2А = 24А4 и 3С = 34С4 –
вниз, а 2F = 24F4 и 3Е = 34Е4 – вверх. Соединив точки В, А, С, В и D, F, E, D отрезками ломаной, получим развертку боковой поверхности призмы. На любом
из этих отрезков, например, АС и FE, строим натуральные величины нижнего и верхнего оснований призмы – треугольники АВС и DEF. Полученная фигура представляет собой развертку полной поверхности призмы. Нанесем на развертку рассмотренной призмы две точки: точку М, лежащую на ребре АF, и точку N, принадлежащую грани АВDF. Найдем проекцию М4 (рис. 98а) и, отложив на ребре АF развертки от точки 2 отрезок 2М = 24М4 (рис. 98б), получим искомую точку М.
Для нанесения на развертку точки N проведем через нее образующую КL (рис. 98а) и найдем проекцию К4L4 этой образующей, а на ней – проекции N4 точки N и 44 точки 4 = КL 12. На развертке (рис. 98б) вдоль прямой l отложим от точки 1 отрезок 14 = 11 41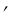 и через точку 4 проведем прямую КL AF. На этой прямой найдем точку N на расстоянии 4N = 44N4.
и через точку 4 проведем прямую КL AF. На этой прямой найдем точку N на расстоянии 4N = 44N4.
Для построения развертки поверхности цилиндра ее обычно аппроксимируют – заменяют вписанной призмой с числом граней не менее двенадцати и
* Замену кривой поверхности вписанной в нее приближенной гранной называют
аппроксимацией поверхности.

|
|
|
S2 |
|
|
|
|
|
|
|
|
|
|
M' |
|
|
|
|
|
|
|
M2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i2 |
|
|
|
|
|
S |
|
|
|
N2 |
N' |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
A2 |
B2 |
D2 |
C2 |
C' |
A' |
D' |
B' |
|
M |
|
|
||||||||
2 |
2 |
2 |
2 |
|
|
||||
|
|
|
S1 |
C' |
A' |
D' |
B' |
|
M |
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
M1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
A1 |
|
|
N1 |
|
|
|
|
A |
C |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
C1 |
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
B1 |
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
б) |
|
|
|
|
|
|
Рис. 97 |
|
|
|

73
F2 L2
D2
E2
M2
 N2
N2
A2
K2 B2 C2
x12
|
|
F1 |
|
|
|
21 |
|
|
E |
|
M1 |
|
L |
1 |
|
|
3' |
||
|
|
|
1 |
|
|
|
41 |
|
1 |
|
|
|
|
|
A1 |
N |
31 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
C1 |
|
D |
|
K1 |
|
1 |
1 |
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
i4 |
B1 |
|
|
|
|
B |
C4 |
|
34 |
|
4 |
|
|
|
|
K4 |
|
|
|
|
A4 |
N4 |
|
14 |
D4 |
|
|
|
||
|
|
|
44 |
|
|
|
M4 |
|
|
|
|
2 |
L4 |
|
|
|
|
||
|
|
|
4 |
F4 |
|
|
|
|
|
|
|
|
4 |
|
а)
2'
1
4'
1
1'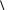
1
1'
3'4
4
 E4
E4
|
|
|
|
D |
|
|
|
|
|
|
E |
|
D |
L |
F |
|
D |
|
|
|
|
|
|
|
l 1 |
4 |
2 |
3 |
1 |
|
|
|
|
M |
|
|
x14 |
N |
|
|
|
|
|
|
|
|
|
4' |
2' |
|
|
|
|
4 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
C |
|
|
B |
K |
|
|
B |
|
A |
|
|
||
|
|
|
|
B
б)
Рис. 98

производят развертку поверхности этой призмы. Полученную развертку принимают за приближенную развертку заданной цилиндрической поверхности.
§ 28. ПРИБЛИЖЕННОЕ ПОСТРОЕНИЕ РАЗВЕРТОК
НЕРАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ
Для того чтобы построить приближенную развертку кривой неразвертывающейся поверхности, эту поверхность аппроксимируют – заменяют приближенной вписанной или описанной многогранной или кривой развертывающейся поверхностью.
ПРИМЕР 34. Построить приближенную развертку сферы (рис. 99). Решение. Рассечем заданную сферу плоскостями , …, проходя-
щими через ее центр О и ось i  1, на некоторое число равных частей*. Эти плоскости пересекут сферу по меридианам. Рассмотрим отсек сферы, заключенный между плоскостями и , и обернем его цилиндрической поверхностью с осью g
1, на некоторое число равных частей*. Эти плоскости пересекут сферу по меридианам. Рассмотрим отсек сферы, заключенный между плоскостями и , и обернем его цилиндрической поверхностью с осью g 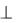 2. Проекция обертывающей поверхности на 2 совпадает с проекцией сферы. Через точки 1, 2, 3 … проведем несколько образующих этой поверхности на одинаковом расстоянии друг от друга (12 = 23 …). На 1 отметим проекции отрезков этих образующих, заклю-
2. Проекция обертывающей поверхности на 2 совпадает с проекцией сферы. Через точки 1, 2, 3 … проведем несколько образующих этой поверхности на одинаковом расстоянии друг от друга (12 = 23 …). На 1 отметим проекции отрезков этих образующих, заклю-
ченных между плоскостями |
и : 11′11″, 21′21″, 31′31″ … Часть указанной |
цилиндрической поверхности, |
заключенной между полуплоскостями и |
, развернем на плоскость. Для этого через произвольную точку А проведем две оси: y x. На оси y отложим отрезки АВ = АЕ = 3222, ВС = ЕF = 2212 … Перпендикулярно оси y отложим от точки
* Обычно таких частей берут не менее 12, но на рис. 99 для наглядности построений взято 6.

|
|
|
|
75 |
|
|
|
|
12 |
|
i2 |
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
y |
D |
|
|
|
|
|
|
|
32 |
|
|
O |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
C'' |
|
C' |
|
|
|
|
g2 |
C |
|
|
|
|
|
|
|
|
|
42 |
|
|
B'' |
|
B' |
|
|
52 |
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
A'' |
|
A' |
|
|
|
|
|
A |
x |
|
|
|
|
|
|
|
1 |
3'' |
|
|
E'' |
|
E' |
|
|
|
|
|
|
|
|
1 |
2''1 |
|
|
E |
|
|
|
|
|
|
||
|
|
1'' |
F'' |
|
F' |
|
31 |
2 |
1 |
O1 |
F |
|
|
|
|
1 |
1 |
|
|
|
|
|
41 |
51 |
i1 |
|
|
|
|
|
1' |
|
|
|
|
|
2'1 |
|
|
G |
|
1 |
|
|
|
|
|
|
3' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
g1 |
|
|
Рис. 99
А отрезки АА′ = АА″ = 3131′, от точек В и Е – отрезки ВВ′ = ВВ″ = ЕЕ′ = ЕЕ″ = = 2121′ … Соединив полученные точки D, С′, В′, А′ … и D, С″, В″ … двумя плавными кривыми, пересекающимися в точках D и G, получим приближенную развертку части сферы, заключенной между полуплоскостями и . Таких разверток должно быть построено столько, на сколько частей разделена сфера меридиональными плоскостями , … (в рассмотренном случае – 6).
ПРИМЕР 35. Дана косая плоскость, заданная направляющими АВ и СD и плоскостью параллелизма (рис. 100а). Построить приближенную развертку части этой поверхности, ограниченной направляющими и крайними образующими АС и ВD.
Решение. Проведем несколько образующих косой плоскости: 12, 34 … Образующие вместе с направляющими составят пространственные четырехугольники: АС21, 1243 … Разделим их диагоналями А2, 14 … на треугольники АС2, А21 … Эти плоские треугольники составят гранную поверхность, аппроксимирующую заданную кривую поверхность. Определив любым способом, натуральные величины сторон указанных треугольников, построим их по трем сторонам (рис. 100б). Заменив ломаные линии А1, 13 … и С2, 24 … плав-

76
B |
|
|
C2 |
|
2 |
|
|
|
|
|
52 |
|
22 |
|
|
3 |
42 |
|
|
|
2 |
|
|
|
|
1 |
62 |
A |
C |
|
2 |
|
|
|
|
A2 |
D2 |
1 |
2 |
x |
A1 |
|
|
|
|
|
3 |
4 |
|
|
|
|
|
|
|
11 |
|
|
|
|
31 |
|
5 |
6 |
|
|
|
|
|
|
51 |
|
C1 |
|
|
|
B |
D |
|
|
|
|
||
|
|
|
21 |
|
B1 |
|
41 |
|
|
|
|
|
|
|
|
|
61 |
|
|
|
|
D1 |
|
|
|
|
1 |
|
|
|
а) |
|
|
б) |
Рис. 100
ными кривыми, получим искомую развертку.
§ 29. КАСАТЕЛЬНЫЕ ПЛОСКОСТИ
На некоторой поверхности (рис. 101) возьмем произвольную точку А. Проведем через нее несколько кривых а, b …, принадлежащих поверхности , и к каждой из них построим в точке А касательные прямые m, n … В курсе высшей математики доказывается, что такие прямые (m, n …) лежат в одной плоскости. Эту плоскость называют касательной плоскостью к поверхности
в выбранной точке. Следовательно, касательная плоскость определяется двумя прямыми (m и n), каждая из которых является касательной к произвольной кривой (а и b), проведенной на данной поверхности ( ) через данную точку (А). Прямая АΝ*, проведенная через точку А перпендикулярно плоскости, касательной к данной поверхности, называется нормалью к этой по-
верхности в данной точке. В случае линейчатой поверхности одной из прямых, определяющих касательную плоскость к этой поверхности, может слу-
* На рис. 101 прямая AN не показана.

|
77 |
|
|
|
|
|
жить образующая l, прове- |
||
n |
|
денная через данную точку. |
||
|
|
Таким образом, плоскость, |
||
|
|
касательная |
к |
линейчатой |
A |
m |
поверхности |
в |
какой-либо |
a |
|
точке А, касается данной по- |
||
|
|
верхности не в одной точке, а |
||
b |
|
по всей образующей l, про- |
||
|
|
веденной через эту точку. |
||
|
|
ПРИМЕР 36. Построить |
||
|
|
плоскость |
, касательную к |
|
|
|
шару в точке К, лежащей на |
||
Рис. 101 |
|
его поверхности. Точка К за- |
||
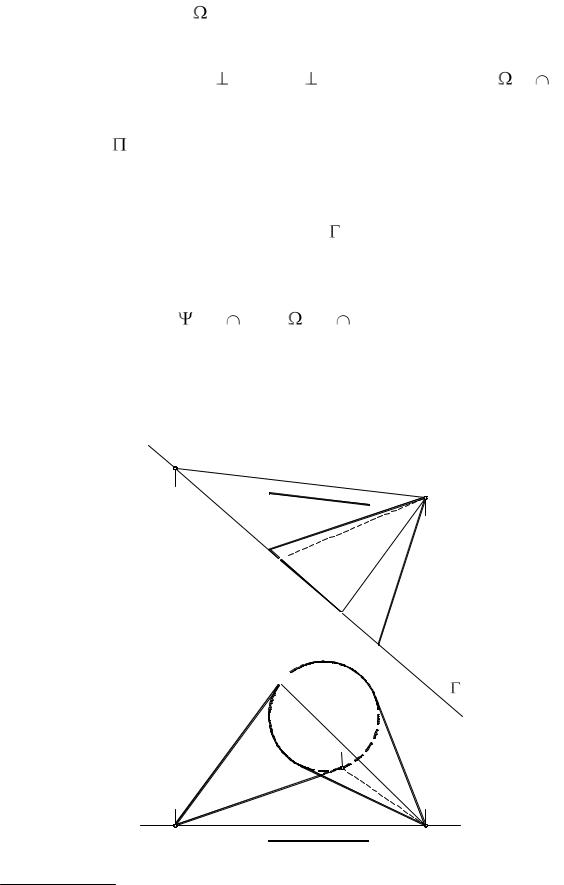
дана одной проекцией К2 (рис. 102).
Решение. Чтобы найти вторую проекцию К1 точки К, проведем через эту
точку плоскость уровня 1. Ее след 2 пройдет через К2. Плоскость |
пе- |
ресечет поверхность шара по окружности l с центром С и радиусом АС. На |
1 |
эта окружность спроецируется в натуральную величину (l1). Проекцию К1 найдем на l1 с помощью линии связи.
|
|
|
|
|
|
S2 |
|
2 |
A2 |
C2 |
K2 |
h2 |
|
|
|
|
l2 |
|
|
|
|
K2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
L2 |
|
|
O2 |
|
f2 |
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
B2 |
|
|
|
|
|
|
|
|
A1 |
|
|
O1 |
C1 |
|
|
B1 |
|
|
A |
|
h |
1 |
|
||
|
1 |
|
|
|
|
|
|
|
l1 |
|
K1 |
|
|
|
|
|
|
|
|
|
|
f1 |
|
|
|
|
|
|
|
S1 |
|
|
|
|
|
|
|
K1 |
L1 |
|
|
|
|
|
|
|
|
|
|
Рис. 102 |
|
|
|
Рис. 103 |
|
78
Искомая плоскость должна быть перпендикулярна радиусу шара ОК. Зададим эту плоскость двумя пересекающимися прямыми, при этом каждая из них будет перпендикулярна ОК. Проще всего за эти прямые принять горизонталь h и фронталь f, тогда h1 О1К1 и f 2 О2К2*. Следовательно, (h f).
ПРИМЕР 37. Построить плоскость, касательную к конусу и проходящую через точку К, не лежащую на его поверхности. Основание конуса лежит в плоскости 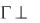 2 (рис. 103).
2 (рис. 103).
Решение. Плоскость касается конуса всегда по его образующей и, следовательно, проходит через вершину. Поэтому в данной задаче нужно через вершину S конуса и заданную точку К провести прямую КS, а через нее – искомую плоскость. Найдем точку L = SK  . Из L1 проведем касательные L1А1 и L1В1 к горизонтальной проекции основания конуса и найдем фронтальные проекции А2 и В2 точек касания А и В. Образующие АS и ВS являются линиями касания плоскостей SLA и SLB с конусом. Следовательно, в данном случае искомых плоскостей две: (АS LS) и (ВS LS).
. Из L1 проведем касательные L1А1 и L1В1 к горизонтальной проекции основания конуса и найдем фронтальные проекции А2 и В2 точек касания А и В. Образующие АS и ВS являются линиями касания плоскостей SLA и SLB с конусом. Следовательно, в данном случае искомых плоскостей две: (АS LS) и (ВS LS).
Так как цилиндр можно рассматривать как конус с бесконечно удаленной вершиной, то задача проведения плоскости, касательной к цилиндру и проходящей через точку К, находящуюся вне его, решается аналогично.
ПРИМЕР 38. Построить плоскость, касательную к конусу и параллельную прямой а (рис. 104).
L2
b2 |
|
a2 |
S2 |
|
A2 
B2 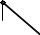
A1 




2
B1
b1
L1 |
a1 |
S1 |
Рис. 104
* См. § 15, рис. 49.
|
79 |
Решение. Через вершину конуса S проводим прямую b a (b1 а1 и |
|
b2 а2) и находим точку L = b |
, где – плоскость основания конуса. |
Через точку L1 проводим две касательные L1А1 и L1В1 к проекции основания конуса. Эти касательные являются линиями пересечения плоскости с двумя плоскостями SLA и SLB, касательными к конусу. При заданном положении конуса и прямой задача имеет два решения*.
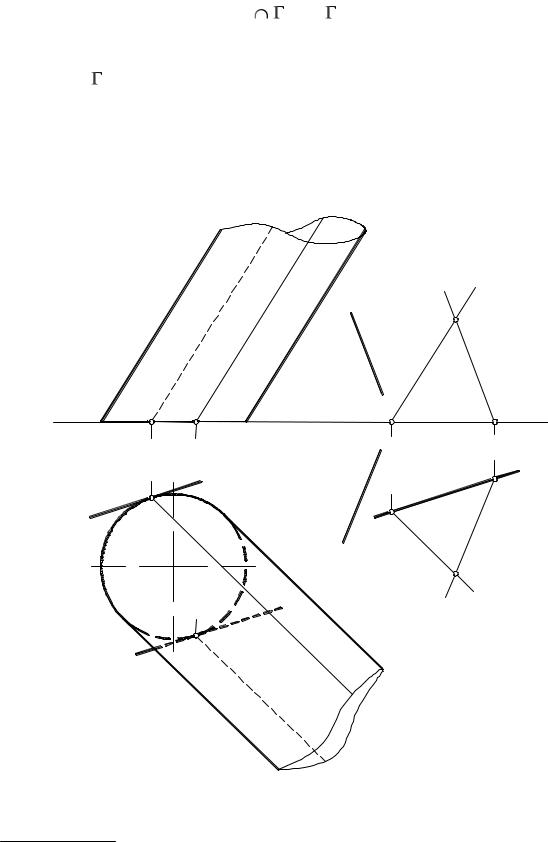
ПРИМЕР 39. Провести плоскость, касательную к цилиндру и параллельную прямой а (рис. 105).
|
p q |
|
b2 |
c2 |
||
|
2 |
2 |
|
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
K2 |
|
|
|
|
|
|
|
A2 B2 |
|
|
N2 |
l2 |
M2 |
|
x |
|
|
|
|
|
|
A1 |
|
|
a1 |
l |
1 |
M1 |
|
|
|
|
|||
|
|
|
|
|
||
s1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N1 |
|
|
|
|
|
|
|
|
|
K1 |
|
|
|
|
b1 |
|
c1 |
B |
1 |
|
p1 |
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q1 |
|
|
|
Рис. 105
* Если заданная прямая параллельна одной из образующих конуса, то задача имеет единственное решение. Если же эта прямая наклонена к плоскости основания конуса под углом, большим угла наклона любой его образующей, то задача не имеет решения.

80
Решение. Через произвольную точку К проведем две прямые: b a и с
– параллельно образующим цилиндра. Найдем горизонтальные следы М1 и N1 этих прямых. Соединив точки М1 и N1, получим горизонтальный след l1 вспомогательной плоскости (b с). Искомая плоскость должна быть параллельна плоскости , а ее горизонтальный след, касательный к основанию цилиндра, – параллелен l1. Таких плоскостей будет две: и . Проведем две касательные s1 и t1 к проекции основания цилиндра: s1 – след плос-
кости , t1 – след плоскости . Через точки их касания А1 |
и В1 |
проводим |
проекции p1 и q1 образующих цилиндра. Плоскости (s |
p) и |
(t q) – |
искомые. |
|
|
