Лекция 2. Обратная матрица. Ранг матрицы
Построение обратной матрицы методом
присоединенной. Ранг матрицы. Нахождение ранга матрицы методами окаймляющих миноров
и элементарных преобразований
2.1. Обратная матрица
Далее будут рассматриваться квадратные матрицы. Единичная матрица
1 |
0 |
... |
0 |
|
|
|
0 |
1 |
... |
0 |
|
E = |
|
||||
|
... ... |
|
n строк |
||
... |
... |
||||
|
0 |
0 |
... |
1 |
|
|
|
||||
14424443
nстолбцов
вумножении квадратных матриц порядка n играет роль, аналогичную роли числа единица в умножении чисел:
|
A AE = EA = A . |
|
(2.1) |
|||||
Действительно, пусть |
a11 |
a12 |
... |
a1n |
|
|||
|
|
|||||||
|
a |
a |
22 |
... |
a |
|
|
|
A = |
21 |
|
|
2n |
. |
|||
... ... |
... ... |
|
||||||
|
|
|||||||
|
a |
a |
|
... |
a |
|
|
|
|
n1 |
n2 |
|
nn |
|
|||
Непосредственная проверка дает: |
AE = A . Аналогично EA = A , и |
|||||||
равенство (2.1) справедливо. |
|
|
|
|
|
|
||
Утверждение 1 . Матрица E - единственная матрица, |
||||||||
обладающая свойством (2.1). |
|
|
|
|
|
|
||
Доказательство. Пусть E′ такая, что |
|
|
||||||
A AE |
′ |
|
′ |
|
|
(2.2) |
||
|
= E A = A . |
|
||||||
Рассмотрим произведение EE′.
|
|
|
|
|
EE′ |
= |
E |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
(2.2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EE′ |
= |
|
E = E′. |
|
|
|
|||||
|
|
|
|
|
E′ |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
(2.1) |
|
|
|
|
|
|
|
|
|
Определение 1. Пусть |
A |
- произвольная квадратная матрица. |
||||||||||||||
Матрица B |
называется |
правой |
обратной |
для |
A , |
если AB = E . |
||||||||||
Матрица C называется левой обратной для A , если CA = E . |
||||||||||||||||
Определение |
2. |
Квадратная |
|
матрица |
A |
называется |
||||||||||
вырожденной |
(особенной), |
если |
|
A |
|
= 0 , |
и |
невырожденной |
||||||||
|
|
|||||||||||||||
(неособенной), если |
|
A |
|
≠ 0 . |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Утверждение 2 . Вырожденная матрица не имеет ни правой, ни левой обратной.
Доказательство. Пусть A - вырожденная. Допустим, B - правая
обратная для A , т.е. |
AB = E . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Тогда |
|
AB |
|
= |
|
|
A |
|
|
|
B |
|
= 0 , но |
|
AB |
|
= |
|
E |
|
=1 , - что является |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
теорема 2 |
|
|
|
|
|
|
|
A |
|
=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
из лекции 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
противоречием, следовательно, |
|
A не имеет правой обратной. |
|||||||||||||||||||||
Аналогично доказывается, что A не имеет и левой обратной.
Утверждение 3 . Пусть ∆ - произвольный определитель порядка n . Сумма произведений всех элементов любого столбца (строки) на алгебраические дополнения соответствующих элементов другого столбца (строки) равна нулю.
Доказательство. Пусть
|
a11 |
... |
a1 j |
... |
a1n |
|
∆ = |
a21 |
... |
a2 j |
... |
a2n |
. |
|
... ... ... ... ... |
|
||||
|
an1 |
... |
anj |
... |
ann |
|
В силу теоремы о разложении по строке (лекция 1, теорема 1) имеем
∆ = a1 j A1 j + a2 j A2 j +... + anj Anj ,
где Akj - алгебраическое дополнение к элементу akj .
Пусть b1,b2 ,...,bn - произвольные вещественные числа. Рассмотрим сумму S = b1A1 j +b2 A2 j +... +bn Anj .
Привлекая ту же теорему о разложении по строке, можем записать
|
|
|
|
a11 |
|
... |
b1 |
|
... |
a1n |
|
|
|
|
|||
|
|
|
S = |
a21 |
|
... |
b2 |
|
... |
a2n |
|
|
|
|
|||
|
|
|
|
... ... ... ... ... |
. |
|
|||||||||||
|
|
|
|
an1 |
|
... |
bn |
|
... |
ann |
|
|
|
|
|||
|
|
|
|
|
|
|
|
j-й |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
столбец |
|
|
|
|
|
|
|
||||
Возьмем в качестве чисел |
bk , |
k =1,..., n , |
элементы i-го столбца |
||||||||||||||
определителя ∆ , i ≠ j , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
S = a |
A |
+ a |
A |
|
+... + a |
A |
= |
|
|||||||
|
|
|
1i |
1 j |
|
2i |
2 j |
|
|
|
ni |
|
nj |
|
|||
|
a11 |
... |
a1i ... |
a1i ... |
a1n |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||||||||
= |
a21 |
... |
a2i ... |
a2i ... |
a2n |
|
|
|
|
= |
0. |
||||||
|
... ... ... ... |
... ... |
... |
|
|
|
свойство |
|
|||||||||
|
a |
... |
a |
... |
a |
|
... |
a |
nn |
|
определителя |
|
|||||
|
n1 |
|
ni |
|
|
ni |
|
|
|
|
|
|
|
|
|
||
|
|
|
i-й |
|
|
|
j-й |
|
|
|
|
|
|
|
|
|
|
|
|
столбец |
|
столбец |
|
|
|
|
|
|
|
|
|||||
Утверждение 3 доказано. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Переходим к построению обратной матрицы методом присоединенной. Пусть A - невырожденная матрица порядка n :
|
|
a11 |
a12 |
... |
a1n |
|
|
||
|
|
a |
a |
... |
a |
|
|
||
A |
= |
|
21 |
22 |
|
2n |
|
. |
|
... ... |
... ... |
|
|||||||
|
|
|
|||||||
|
|
a |
a |
... |
a |
|
|
||
Матрица |
|
|
n1 |
n2 |
|
nn |
|
|
|
|
A11 |
A21 |
... |
An1 |
|
||||
|
|
|
|||||||
|
|
|
A |
A |
... |
A |
|
|
|
= |
|
12 |
22 |
|
n2 |
||||
A |
... |
... |
... ... |
|
|
||||
|
|
|
|||||||
|
|
|
A |
A |
... |
A |
|
|
|
|
|
|
1n |
2n |
|
nn |
|||
называется присоединенной для A . Элементами матрицы A являются алгебраические дополнения к элементам матрицы A , причем
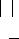
алгебраические дополнения к элементам i-й строки матрицы помещены в i-й столбец A .
Обозначим A = ∆ .
Матрица B = ∆1 A является правой и левой обратной для A .
Действительно,
|
|
|
|
|
|
∆ |
0 ... |
0 |
1 |
0 |
... |
0 |
|
|
||
1 |
|
|
1 |
|
0 |
∆ ... |
0 |
|
0 |
1 |
... |
0 |
|
|
||
AB = A |
|
A |
|
= |
|
|
|
... ... |
|
= |
|
... |
... |
|
|
= |
∆ |
|
|
|
|
||||||||||||
|
|
|
теорема о |
∆ ... |
... |
... |
... |
|
||||||||
|
|
|
|
разложении по строке |
|
|
0 |
0 ... |
|
|
0 |
0 |
... |
1 |
|
|
|
|
|
|
и утверждение 3 |
|
|
∆ |
|
|
|
||||||
A
E.
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
Следовательно, матрица |
B = |
|
|
A |
- |
правая обратная для A . |
|||||||||||
∆ |
|||||||||||||||||
Аналогично |
1 |
A A = E , и матрица B = |
1 |
A |
является и левой обратной |
||||||||||||
∆ |
∆ |
||||||||||||||||
для A . Она называется обратной для A и обозначается A−1 . |
|||||||||||||||||
Итак, |
|
|
|
|
A |
A ... |
|
A |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
11 |
21 |
|
|
|
|
n1 |
|
|
||
|
|
A |
−1 |
= |
1 |
A12 |
A22 ... |
|
An2 |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
∆ ... ... ... |
|
... |
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
A |
A |
... |
|
A |
|
|
||||
|
|
|
|
|
|
|
1n |
|
2n |
|
|
|
|
nn |
|
|
|
Утверждение 4 . Матрица |
A−1 - единственная |
обратная |
||||||||
для A . |
|
|
|
|
|
|
|
|
|
|
Действительно, допустим, C такая, что CA = AC = E . |
|
|||||||||
Рассмотрим CAA−1 = C (AA−1 ) |
= CE = C . |
С |
|
другой |
стороны, |
|||||
CAA−1 = (CA)A−1 = EA−1 = A−1 , следовательно C = A−1 . |
|
|||||||||
Пример 1. Найти |
|
|
|
|
|
2 |
8 |
|
|
|
A−1 для матрицы A = |
3 |
7 |
. |
|
||||||
|
|
|
|
|
|
|
|
|
||
Решение. Имеем |
∆ = |
|
A |
|
=14 −24 = −10 ≠ 0 , |
следовательно, A−1 |
||||
|
|
|||||||||
существует.
Находим алгебраические дополнения к элементам матрицы A и составляем присоединенную матрицу:
|
|
7 |
−8 |
|
A11 = 7, A12 = −3, A21 = −8, A22 = 2, A |
= |
−3 |
2 |
. |
|
|
|
Откуда A−1 = − |
1 |
|
7 |
|
|
−8 |
|
−0,7 |
0,8 |
|
|
||||||||
|
|
|
|
|
−3 |
|
|
|
= |
0,3 |
−0, 2 |
. |
|
|
|||||
10 |
|
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||
Пример 2. Решить матричное уравнение |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
8 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
X = |
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
2 |
3 |
|
|
|
|
Решение. Обозначим |
|
|
A = |
|
2 |
4 |
8 |
1 |
. Тогда исходное |
||||||||||
|
|
|
3 |
, |
B = |
2 |
|
||||||||||||
уравнение принимает вид |
|
|
|
|
7 |
|
3 |
|
|||||||||||
|
|
AX = B . |
|
|
|
(2.3) |
|||||||||||||
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A |
|
= |
|
|
2 4 |
|
=14 −12 = 2 |
≠ 0 A−1 . |
||||||||||
|
|
|
|
||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Домножим обе части уравнения (2.3) слева на матрицу A−1 и получим
X = A−1B .
Итак,
A−1 |
= |
1 |
|
7 |
−4 |
|
, |
|
|
|
−3 |
2 |
|
||||
2 |
||||||||
|
|
|
|
|
X = |
1 |
7 |
−4 8 |
1 |
|
1 |
56 −8 |
7 −12 |
24 |
−5 / 2 |
||||||||||
|
|
−3 |
2 |
|
2 |
3 |
|
= |
|
|
−24 |
+ 4 |
−3 +6 |
|
= |
−10 |
3/ 2 |
. |
||
2 |
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
Упражнения. |
|
Докажите следующие свойства обратной |
||||||||
матрицы. |
|
|
|
|
1 |
|
||||
1. Если ∆ = |
|
A |
|
, то |
|
A−1 |
|
= |
. |
|
|
|
|
|
|||||||
|
|
|||||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
||
2.(AB)−1 = B−1 A−1 .
3.(AT )−1 = (A−1 )T .