Лекция 7. Линейные операторы

7.1. Понятие линейного оператора

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Rzavinskay.pdf

Скачиваний:

564

Добавлен:

27.03.2016

Размер:

1.92 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1412 13 14 > Следующая >>>

Линейный оператор - определение и примеры. Матрица линейного оператора. Собственные числа и собственные векторы. Линейные операторы с простым спектром

(Q −λE)x = θ .

При λ1 =1 имеем Q −λ1E =

. Подставим ее в (7.3):

При λ1 =1 имеем Q −λ1E =

. Подставим ее в (7.3):

Определение 1. Пусть V - линейное пространство и каждому вектору x , принадлежащему V , поставлен в соответствие вектор y ,


y V .	Соответствие			A : x → y	называется	оператором,
определенным в линейном пространстве V .
Принята		также	запись: y = A(x) . Вектор x			называется
прообразом, а y - образом при отображении оператором A .
Определение 2.			Оператор A ,		определенный	в линейном
пространстве V , называется линейным, если:
1)	x V	y V	A(x +y) = A(x) + A(y) ;

2) x V λ - вещественного числа A(λx) = λA(x) .

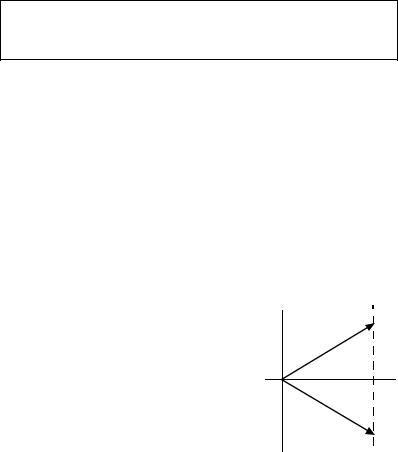
Пример 1. V - линейное пространство всех геометрических векторов

плоскости, A	- зеркальное	отражение
относительно	оси Ox (рис.	7.1). A -

линейный оператор.

Убедимся, что выполняется требование 2) в определении 2.

Пусть λ - произвольное вещественное

число,		по определению умножения на λ для
геометрического вектора x , вектор							uuur
геометрического вектора x , вектор							OB = λx
имеет		то		же направление, что и			x , если
λ > 0 ,		и			противоположное, если		λ < 0 ,
	uuur
и	OB	=	λ		x	.

A(x)

Рис. 7.1.

Рис. 7.2 соответствует случаю	λ > 0 ,	λ	>1 ( λ < 0
Рис. 7.2 соответствует случаю	λ > 0 ,	λ	>1 ( λ < 0
рассматривается аналогично).

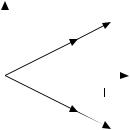
uuur

зеркальное отражение вектора

uuur

Пусть OK = x ,

OB = λx ,

относительно оси Ox ,

uur

- зеркальное отражение вектора

uur

OB .

uuur

Тогда

∆OKP

~ ∆OBD

и,

значит,

Но

uuur

uur

поэтому

Кроме

того,

направление

вектора

совпадает

с направлением вектора

uuur

uur

uuur

OD ,

следовательно, OD = λ OP .

Таким образом, имеем

uuur

OP = A(x)

uuur

= A(λx)

A(λx)

= λA(x) .

uuur

= λ OP

C x

Также, исходя из геометрических

соображений,

можно

доказать,

что

A(x +y) = A(x)

+ A(y) ,

следовательно,

оператор

зеркального

отражения

Рис. 7.2.

относительно

оси

является

линейным

оператором.

Упражнения.

V ={Pn (x)}- линейное пространство всех многочленов степени

≤ n ,

A -

оператор дифференцирования,

A : Pn (x) → Pn′(x) .

Доказать,

что A - линейный оператор.

V = C[a,b]- линейное пространство всех непрерывных на отрезке

[a,b] функций. Для

любой

f (x) V оператор

определен

следующим равенством:

A( f (x)) = ∫f (t)dt , x [a,b].

Доказать, что A - линейный оператор.

Определение 3.

Пусть

V - линейное пространство, e1,e2 ,...,en -

базис

V ,

A - линейный оператор

V . Матрицей

линейного

оператора A в базисе e1,e2 ,...,en называется матрица			Q =	aij	,
i, j =1,.., n , такая, что
A(e1) = a11e1	+a21e2	+... + an1en ,
A(e2 ) = a12e1	+ a22e2	+... + an2en ,
……………………………………..			(7.1)

A(en ) = a1ne1 +a2ne2 +... + annen .

Замечание 1 . Столбцы матрицы Q являются координатами в разложении векторов A(e1), A(e2 ),..., A(en ) по базису e1,e2 ,...,en .

Пример 2. Найти матрицу линейного оператора зеркального отражения относительно оси Ox в базисе i, j .

Решение.	По	определению оператора
A A(i) = i, A(j) = −j (рис. 7.3).
Используя	разложение векторов		A(i) и
A(j) по базису i, j ,		находим: A(i) = i ={1,0},
A(j) = −j ={0, −1}.		Полученные	строки
координат располагаем по столбцам:

y
	j
	i=A(i)
O	x

-j=A(j)

1	0	Рис. 7.3.
Q =	.
0	−1
Упражнение. V3 - линейное пространство всех геометрических
векторов, i, j,k - декартов базис, Oxyz		- декартова система координат,

A - оператор проектирования на ось Ox . Доказать, что A - линейный оператор, и найти его матрицу в базисе i, j,k .

Замечание 2 . Пусть V - линейное пространство, A - линейный оператор в V , e1,e2 ,...,en (I) - базис в V . Матрица оператора в базисе

(I) определена однозначно.

Для того, чтобы в этом убедиться, разложим векторы A(e1), A(e2 ),..., A(en ) по базису (I). Столбцы матрицы Q представляют

собой координаты этих векторов, которые согласно теореме 3 лекции 5 определяются единственным образом, следовательно, матрица Q

оператора A в (I) определена однозначно.

Теорема 1. Пусть

V - линейное пространство, e1,e2 ,...,en

(I)

базис в V , A - линейный оператор

V ,

Q =

aij

, i, j, =1,..., n

матрица

линейного

оператора

базисе

(I),

x V ,

x = x1e1 +... + xnen , y = A(x) ,

y = y1e1 +... + ynen . Тогда

...

= Q ...

Доказательство. Имеем

y = A(x) = A(x e +... + x e

)

x A(e ) +... + x A(e

) =

1 1

А − линейный 1

)

x A(e

a e

x a e

∑ i

(7.1) ∑ i

∑ ki

вносим xi под

∑

∑ i

i=1

k =1

знак внутренней суммы i=1

k =1

x a e

x a

меняем порядок

∑ ∑ i ki

выносим ел за

∑

∑ i ki

суммирования

k =1 i=1

знак внутренней. суммы k =1 i=1

По условию y = y1e1 +... + ynen = ∑yk ek .

k =1

Используя теорему о единственности разложения вектора по базису (теорема 3 из лекции 5), получим

	n
k, k =1...n, yk = ∑xi aki =x1ak1 + x2ak 2 +... + xnakn .					(7.2)
	i=1
Заметим, что в последнем			равенстве числа ak1, ak 2 ,..., akn -
элементы k-й строки матрицы Q .
Учитывая правило умножения матриц, равенство (7.2) запишем в
виде
	y		x
		1	1
...			= Q ...	.
y		n	x
		n	n

Теорема доказана.

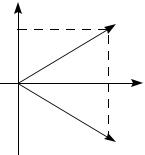
Пример

3. Для

линейного

оператора зеркального

отражения

относительно оси Ox найти, как

преобразуются

координаты

произвольного вектора.

Решение. Матрица оператора была

x={x1, x2}

найдена в примере 2:

Q =

−1

В силу теоремы 1, если

x = x1

прообраз, а

y = A(x)

образ,

y = y1 ,

A(x) ={x1,− x2}

0 x1

то y

−1 x

−x

то есть

Рис. 7.4.

первая координата образа остается без изменения, а вторая меняет лишь

знак (рис. 7.4).

Пример

V ={P2 (x)}-

линейное

пространство

всех

многочленов степени ≤ 2 ,

A - линейный оператор дифференцирования.

Найти

его

матрицу

базисе

1, x, x2

и, используя теорему 1,

продифференцировать многочлен

= −3x2 +4x −7 .

Решение. Находим образы векторов базиса

A(ei )

разлагаем

полученные векторы по базису 1, x, x2 :

A(e ) = A(1) = (1)′ = 0 = (0,0,0) ,

A(e2 ) = A(x) = (x)′ =1 = (1,0,0) ,

A(e3 ) = A(x2 ) = (x2 )′ = 2x = (0, 2,0) .

Матрица оператора A в базисе 1, x, x2

имеет вид

Q =

					−7							β
а вектор P	= −3x2	+4x −7 =				4	.	Обозначим			A(P ) =		β1	. По
2											2		2
						−3							β
													3
теореме 1 имеем
		β	0		1		0	−7		4
		1		0	0		2	4		−6	,
		β2	=	0	0		2	4	=	−6	,
		β		0	0		0	−3		0
		3

или в виде разложения по базису 1, x, x2 : A(P2 ) = 4 −6x .

Упражнение. V2 - линейное пространство всех геометрических векторов плоскости, i,j - декартов базис, Oxy - декартова система

координат, A - оператор поворота плоскости вокруг начала координат на угол ϕ = π3 против часовой стрелки. Доказать, что A - линейный

оператор, найти матрицу Q оператора A в базисе i,j и координаты образа вектора x ={1, 2}.

7.2. Собственные векторы и собственные значения линейного оператора

Определение 4. Квадратные матрицы B и C называются подобными, если существует невырожденная матрица Q , такая, что

		C = Q−1BQ .
Теорема 2. Пусть V - линейное пространство,			e1,e2 ,...,en	(I) и
e1′,e′2 ,...,e′n (II) - два базиса в V , T - матрица перехода от (I) к (II),					A
- линейный оператор в V , B - матрица оператора A в (I),				C	-
матрица оператора A в (II). Тогда
		C =T −1BT .
Это утверждение примем без доказательства.
Пусть A =	aij	, i, j, =1...n . Матрица A −λE , где	E - единичная
Пусть A =	aij	, i, j, =1...n . Матрица A −λE , где	E - единичная

матрица порядка n , а λ - произвольное вещественное число,

называется характеристической матрицей для A . Она имеет вид

	a11 −λ		a12			...		a1n
		a	a		−λ	...		a
A −λE =		21	22					2n	.
A −λE =	....		...			...		...	.
	....		...			...		...
		a	a	n2		...	a	−λ
		n1		n2				nn

Определитель

A −λE

- некоторый

многочлен

порядка

относительно λ.

Определение

Многочлен

A −λE

называется

характеристическим

многочленом

матрицы A , а

его корни

характеристическими корнями матрицы A .

Теорема 3. Подобные матрицы имеют одинаковый набор

характеристических корней.

Доказательство. Пусть C = Q−1BQ , Q - невырожденная матрица.

Имеем

C −λE

Q−1BQ −λE

Q−1BQ −Q−1(λE)Q

Q−1(B −λE)Q

Q−1

B −λE

свойства

теорема об

умножения

определителе

матриц

произведения

матриц

Характеристические многочлены матриц В и С совпадают, следовательно, совпадают и характеристические корни.

Теорема доказана.

Следствие. Матрицы, задающие линейный оператор в различных базисах, имеют один набор характеристических корней. (Теорема 2 +

теорема 3.)

Определение 6. Характеристические корни матрицы линейного оператора (в любом базисе) называются характеристическими корнями линейного оператора.

Определение 7. Весь набор характеристических корней называется спектром оператора.

Определение 8. Пусть V - линейное пространство, A - линейный оператор в V . Вектор x ≠ θ называется собственным вектором оператора A , если найдется действительное число λ, такое, что

A(x) = λx .

Число λ называется собственным значением, соответствующим данному собственному вектору x .

Справедливо следующее утверждение, которое приведем без доказательства.

Теорема 4. Действительные характеристические корни линейного оператора, если они существуют, и только они, служат собственными значениями линейного оператора.

Пример 5. Найти собственные векторы и собственные значения линейного оператора зеркального отражения относительно оси Ox .

Матрица оператора была найдена в примере 2:						1	0
Матрица оператора была найдена в примере 2:						Q =	.
Составляем характеристическое уравнение:						0	−1
Составляем характеристическое уравнение:
	Q −λE	=	1−λ	0	= 0 ,


			0	−1−λ
			0	−1−λ
откуда (1−λ)(−1−λ) = 0 и λ1 =1 , λ2 = −1 .
Числа λ1 =1 , λ2 = −1 -			характеристические корни				линейного

оператора (в соответствии с определением 6), они действительны и, согласно теореме 4, являются собственными значениями. Найдем соответствующие им собственные векторы.

По определению собственного вектора x A(x) = λx , но A(x) = Qx , следовательно, ищем векторы, удовлетворяющие уравнению Qx = λx , или Qx = λEx , или

что равносильно системе уравнений

0		x	+0 x	= 0,	(7.4)
	0	1	2	= 0,	(7.4)
	0	x	−2 x	= 0,
		1	2

откуда x2 = 0 , и решением системы (7.4) являются все векторы вида

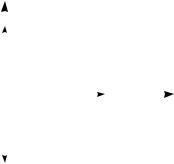
	X (1) = c1		,
	0
c1 - произвольное вещественное число, отличное от нуля.
При λ2 = −1 получаем Q −λ2 E =			2	0		, подставляем в (7.3):
При λ2 = −1 получаем Q −λ2 E =			0	0		, подставляем в (7.3):
			0	0
2	0 x1		0
0	0 x	=		0	,
	2
получаем систему уравнений
2 x1 +0 x2 = 0,
0	x +0 x		= 0,
	1	2

откуда X (2) =	0		,	с - произвольное вещественное число, отличное
		с		2
		2

от нуля.

Геометрически это означает, что любой ненулевой вектор,

приложенный		к началу координат			с концом на	оси Ox , является
собственным,		отвечающим		y
собственному		значению

λ1 =1 (действие на			него
оператора	A	сводится к			A(y)
умножению его на λ1 =1 , а
любой ненулевой вектор с					x =A(x) - собств., λ = 1
концом на оси		Oy является

				O			x
собственным,		отвечающим

собственному		значению			y - собств.,	λ = –1
λ2 = −1	(то есть действие

оператора	A	на	этот

вектор	заключается		в		Рис 7.5.
умножении его на λ2 = −1

(рис. 7.5)).

Упражнение. V - линейное пространство всех геометрических векторов, A - линейный оператор проектирования на ось Ox . Найти все его собственные числа и собственные векторы.

7.3. Приведение матрицы линейного оператора к диагональному виду путем перехода к новому базису

Линейный оператор A задается в базисе e1,e2 ,...,en (I)

диагональной матрицей тогда и только тогда, когда все векторы базиса

(I) - собственные.

Действительно, пусть e1,e2 ,...,en (I) - собственные векторы, отвечающие собственным значениям λ1, λ2 ,..., λn соответственно, то

есть

A(e1) = λ1e1 , A(e2 ) = λ2e2 ,

………………. (7.5)

A(en ) = λnen .

Из равенств (7.5) следует справедливость разложений по базису (I):

A(e1) = λ1 e1 +0 e2 +... +0 en , A(e2 ) = 0 e1 +λ2 e2 +... +0 en ,

…………………………………….

A(en ) = 0 e1 +0 e2 +... +λn en ,

и по определению матрицы оператора (определение 3) имеем

λ1		0 ...	0
	0	λ2 ...	0		(7.6)
Q =	0	0 ...	0	,

	0	0 0
			λn
то есть матрица Q оператора		A в (I)	- диагональная (по диагонали
стоят собственные значения).
Обратно. Пусть Q - матрица оператора A					в базисе (I) имеет
диагональный вид (7.6), следовательно,			A(e1) = λ1e1 ,…, A(en ) = λnen и,
таким образом, векторы ei ,	i =1,..., n -		собственные с собственными
значениями λi , i =1,..., n .

Вопрос о том, можно ли линейный оператор задать в некотором базисе диагональной матрицей, равносилен вопросу о том, существует ли для данного оператора базис, состоящий из собственных векторов.

Теорема 5. Пусть V -		линейное пространство, A - линейный
оператор в V , b1,b2 ,...,bk		- собственные векторы оператора A ,
отвечающие	собственным	значениям	λ1, λ2 ,..., λk .	Если

i j, i ≠ j λi ≠ λ j , то b1,b2 ,...,bk - линейно независимы.

Доказательство. Доказательство проведем индукцией по числу

векторов k .
При k =1 имеем один вектор b1 ≠ θ	(по определению

собственный вектор отличен от нулевого), вектор b1 составляет

линейно независимую систему.

Пусть утверждение теоремы справедливо для k −1 : всякая система

k −1 собственных

векторов,

отвечающих

различным

собственным

значениям, является линейно независимой.

Пусть имеется

система

собственных векторов

b1,b2 ,...,bk ,

относящихся

различным

собственным

значениям

λ1, λ2 ,..., λk

( i j, i ≠ j λi ≠ λ j ).

Предположим, система b1,b2 ,...,bk

линейно зависима,

то есть

найдутся числа α1, α2 ,..., αk ,

не все

равные

нулю,

такие,

что

выполняется равенство

α1b1 +α2b2 +... +αk bk = θ.

(7.7)

Не ограничивая

общности

рассуждений, можем

считать,

что

α1 ≠ 0 (иначе перенумеруем векторы).

Применим к обеим частям равенства (7.7) оператор A :

A(α b +α

+... +α

)

α A(b ) +... +α

A(b

) =

1 1

A - линейный

α λ b +... +α

= A(θ) = θ.

- cобственные,

1 1

i=1,...,n

Из последнего равенства получаем

α1λ1b1 +... +αk λk bk

= θ .

(7.8)

Обе части равенства (7.7), умноженные на λk , вычтем почленно из

обеих частей (7.8), получим

α1(λ1 −λk )b1 +... +αk (λk −1 −λk )bk −1 = θ.

(7.9)

Равенство (7.9) означает, что векторы

b1,b2 ,...,bk −1 -

линейно

зависимы (их линейная комбинация с коэффициентами,

не равными

одновременно нулю, например, коэффициент при b1 отличен от нуля, равна θ ), но это противоречит предположению индукции: векторы b1,b2 ,...,bk −1 - собственные, относящиеся к различным собственным значениям. Следовательно, b1,b2 ,...,bk - линейно независимы, и

утверждение теоремы справедливо при любом k . Теорема доказана.

Определение 9. Линейный оператор A называется линейным оператором с простым спектром, если все его характеристические корни действительны и различны.

Теорема 6. Всякий линейный оператор с простым спектром

может быть задан диагональной матрицей.
Доказательство. Пусть V -				линейное пространство,			dim V = n ,
A -	линейный оператор в V ,			A имеет простой спектр.				Тогда
характеристических корней n .			Пусть это числа λ1, λ2 ,..., λn ,					в силу
теоремы 4 λ1, λ2 ,..., λn		- собственные значения оператора A .
Пусть e1,e2 ,...,en		- соответствующие этим собственным значениям
собственные векторы,		тогда согласно теореме 5 e1,e2 ,...,en					- линейно
независимы, и так как dim V = n , e1,e2 ,...,en						- базис. В этом базисе, как
было отмечено выше, матрица оператора имеет вид
		λ1		0 ...	0
		0		λ2 ...	0
		Q =
		... ... ... ...
				0 ...	λn
		0		0 ...	λn
и является диагональной матрицей.
Теорема доказана.
Пример 6. Линейный			оператор		A	задан своей	матрицей
1	4
B =	в некотором базисе. Выяснить, существует ли для данного
2	3

оператора базис, в котором его матрица имеет диагональный вид. В случае положительного ответа найти этот базис и соответствующую ему матрицу Q .

Решение. Составляем и решаем характеристическое уравнение:

λ2 −4λ−5 = 0 ,

откуда λ1 = 5 , λ2 = −1 - характеристические корни оператора A . Они

вещественны и различны, следовательно, согласно теореме 6 для оператора A существует базис, состоящий из собственных векторов, и в этом базисе матрица оператора имеет вид

							5				0
							Q =					.
							0			−1
	Находим собственные векторы.
	При λ1 = 5 имеем
					−4		4 x1					=	0		,
						2	−2	x				=	0		,
									2
или 2x		−2x		= 0 x	= x	X (1) =			c1			. Все ненулевые векторы вида
	1		2	1	2				c
									1
c1	являются собственными с собственным значением λ = 5 .
c																1
1
	При λ2 = −1 имеем
						2	4	x1				0
						2	4	x			=		0	,
							2
или 2x		+ 4x		= 0 x	= −2x		X (2)			=	−2c2				.	Все ненулевые векторы
	1		2	1		2							c
													2
	−2c			- собственные с собственным значением λ2 = −1 .
вида		c 2		- собственные с собственным значением λ2 = −1 .
		2
	Полагаем c1 = c2 =1 , имеем e1 =									1						−2
	Полагаем c1 = c2 =1 , имеем e1 =									1 , e2					=	1 .

В базисе e1,e2 матрица A оператора имеет вид Q .

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1412 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.201976.29 Кб40readmsg.doc
#
16.09.2019308.22 Кб51referatbank-8720.doc
#
27.03.20162.81 Mб813Rivlina_Blokkh.pdf
#
13.11.2019229.38 Кб14rpd_ib_ib_oib_090900.62.doc
#
21.08.2019517.63 Кб34Ryady_razdat_material.doc
#
27.03.20161.92 Mб564Rzavinskay.pdf
#
05.06.20153.93 Mб137SAVELEVA.pdf
#
05.06.201512.44 Кб35setup OrCAD.docx
#
27.03.2016996.57 Кб85Sharafutdinova_2012.pdf
#
05.06.201519.08 Кб180Short stories. Unit 12. The Dinner Party.docx
#
05.06.201585.5 Кб175Short stories. Unit 4. A Foul Play.doc