6.1. Связь между базисами линейного пространства

системы (I),

то есть найдутся такие числа τij , i, j =1,..., n , что

e1′ = τ11e1 +τ21e2

+... +τn1en

e′2 = τ12e1 +τ22e2

+... +τn2en

……………………………….

(6.1)

e′n = τ1,ne1 +τ2,ne2 +... +τnnen

Определение 1. Матрица T =

τij

, i, j =1,..., n

называется

матрицей перехода от базиса (I) к базису (II).

Замечание 1 . Столбцы матрицы перехода T =

τij

, i, j =1,..., n ,

являются

координатами в разложении векторов e1′,e′2 ,...,e′n по

β

α

1

1

β2

=T

−1

α2

.

(6.2)

...

...

αn

Доказательство.

βn

Подставим

в

разложение x по базису (II)

выражения ei′,

i =1, 2,..., n

из (6.1), получим

x = β e′

+β

e′ +... +β

e′

=

n

n

β

n

τ

=

β e′=

∑

e

1 1

2

2

n

n

∑ i i

1 ∑

i

ki

k

вносим βi

под знак

i=1

i=1

k =1

внутренней суммы

=

n

n

β τ

e

=

n

n

β τ

e

=

ki

ki

∑

∑ i

k

меняем порядок∑

∑ i

k

выносим e

i=1

k =1

суммирования

k =1

i=1

за знак

k

внутренней суммы

n

n

= ∑

∑βiτki ek .

k =1

i=1

Последнюю сумму запишем развернуто:

n

n

n

n

n

∑

∑βi τki ek

=

∑βiτ1i e1 +

∑βi τ2i e2

+... +

∑βiτni en =

k =1

i=1

i=1

i=1

i=1

= (β1τ11 +β2τ12 +... +βnτ1n )e1 +(β1τ21 +β2τ22 +... +βnτ2n )e2 +... +

+(β1τn1 +β2τn2 +... +βnτnn )en .

По

условию

x = α1e1 +α2e2 +... +αnen ,

используя теорему о

α

β

1

1

α2 =T β2 .

...

...

Отсюда следует

αn

βn

β

α

1

1

β2

=T

−1

α2 .

...

...

Теорема доказана.

βn

αn

Пример 1.

V2

-

линейное пространство всех геометрических

векторов плоскости,

e1,e2 (I) - произвольный декартов базис, e1′,e′2 (II) -

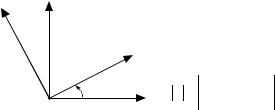
декартов базис, полученный поворотом векторов e1 и e2 на угол ϕ

против хода часовой стрелки. Найти матрицу

перехода от (I) к (II) и

связь координат одного и того же вектора в (I) и (II).

Имеем e′ ={cos ϕ,sin ϕ} ,

e′

={−sin ϕ,cos ϕ}

( рис. 6.1). Тогда

1

2

e

cos ϕ

−sin ϕ

2

T =

.

e2'

e1'

sin ϕ

cos ϕ

T - матрица перехода от (I) к (II).

Найдем T −1 .

ϕ

T = cos ϕ

−sin ϕ

= cos2 ϕ+sin2 ϕ =1 и

Рис. 6.1.

e1

sin ϕ

cos ϕ

sin ϕ

T

−1

cos ϕ

=

.

−sin ϕ

cos ϕ

Формула (6.2) в этом случае имеет вид

β

cos ϕ

sin ϕ

α

,

1

=

−sin ϕ

1

β2

cos ϕ

α2

где α1,α2 - координаты произвольного вектора

x V в базисе (I), а

β1,β2 координаты этого же вектора в базисе (II).

Пример 2. V - произвольное линейное пространство, dim V = 2 .

Векторы e1′ = (1,1) , e′2 = (1, 2)

и x = (6,9)

заданы своими координатами в

λ1+ λ2 = 0,

(6.3)

λ + 2λ

2

= 0.

1

Определитель системы (6.3)

∆ =

1

1

= 2 −1 =1 ≠ 0 , следовательно,

1

2

комбинации равны нулю. Это означает, что система векторов

e1′,e′2

линейно независима,

а

так

как dim V = 2 ,

векторы e1′,e′2 являются

базисом в V . Обозначим этот базис (II).

Найдем матрицу перехода от (I) к (II).

1

1

(координаты векторов e1′

и e′2 в

В силу определения 1 T =

(I) располагаем по столбцам).

1

2

Обозначим (β1,β2 ) координаты вектора x в (II).

Воспользуемся теоремой 1. Найдем T −1 .

2

−1

T

=

1

1

= 2 −1 =1 ,

T −1 =

−1

1

2

1

и по формуле (6.2) получим

β

2

−1

6

12 −9

3

1

=

=

=

.

β2

−1

1

9

−6 +9

3