
- •Лекции по линейной алгебре
- •Предисловие
- •Лекция 1. Матрицы
- •1.1. Основные понятия
- •1.2. Определители порядка n
- •1.3. Основные операции над матрицами
- •Лекция 2. Обратная матрица. Ранг матрицы
- •2.1. Обратная матрица
- •2.2. Ранг матрицы
- •3.1. Метод Гаусса
- •4.1. Правило Крамера
- •Лекция 5. Линейные пространства
- •5.2. Базис линейного пространства
- •6.1. Связь между базисами линейного пространства
- •6.2. Линейные подпространства
- •Лекция 7. Линейные операторы
- •7.1. Понятие линейного оператора
- •Лекция 8. Евклидовы пространства
- •8.1. Понятие евклидова пространства
- •8.2. Ортогональные и ортонормированные базисы в
- •Оглавление

Лекция 8. Евклидовы пространства
Определение евклидова пространства. Ортогональные и ортонормированные базисы. Процесс ортогонализации Шмидта.
8.1. Понятие евклидова пространства
Определение 1. Евклидовым пространством En называется n- мерное линейное пространство, в котором каждой паре векторов x,y
поставлено в соответствие вещественное число, называемое скалярным произведением векторов x и y (это число обозначим
(x,y) ), причем выполняются следующие аксиомы:
I)x En
II) x En III) x En IV) x En
y En (x, y) = (y, x) ;
y En z En (x +y, z) = (x, z) +(y, z) ;
y En λR (λx, y) = λ(x, y) ; x ≠ θ (x, x) > 0 .
Замечание. Аксиомы II и III справедливы также в форме II’: (x, y + z) = (x, y) +(x,z) и III’: (x, λy) = λ(x, y)
Пример 1. Пусть V3 - линейное пространство геометрических векторов, скалярное произведение определено равенством
(x, y) = |
|
x |
|
|
|
y |
|
|
|
(8.1) |
|
|
|
cos x, y . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
Аксиомы I - IV выполняются (см. алгебраические свойства скалярного произведения, доказанные в векторной алгебре), следовательно, со скалярным произведением, определенным равенством
(8.1), V3 является евклидовым пространством.
Пример 2. В линейном пространстве арифметических векторов Rn формула
(x, y) = x1 y1 + x2 y2 +...+ xn yn , |
(8.2) |
где x = (x1 ,x2 ,...,xn ) , y = ( y1 , y2 ,..., yn ) , задает скалярное произведение.
Докажем это. Проверим выполнение аксиом I - IV. Поскольку компоненты xi , yi i =1,..., n - вещественные числа, имеем
(x, y) = x1 y1 +...+ xn yn = y1x1 +... + yn xn = (y,x),
следовательно, аксиома I выполняется.
Пусть z = (z1, z2 ,..., zn ) Rn . По определению сложения в Rn x +y = (x1 + y1, ..., xn + yn ) . Имеем
(x +y, z) = (x1 + y1)z1 +...+(xn + yn )zn =
(8.2)
=(x1z1 + y1z1) +...+(xn zn + yn zn ) =
=(x1z1 +... + xn zn ) +...+( y1z1 +... + yn zn ) = (x, z) +(y, z) ,
аксиома II справедлива.
Пусть λ - произвольное вещественное число. По определению
умножения вектора на число в Rn
λx = (λx1 ,λx2 ,...,λxn ) .
Далее имеем
(λx, y) = (λx1) y1 +...+(λxn ) yn = λ(x1 y1 +...xn yn ) = λ(x,y) , |
|||
(8.2) |
|
|
|
аксиома III выполняется. |
x2 |
+...+ x2. |
|
Проверим выполнение аксиомы IV: (x, x) = |
|||
|
(8.2) |
1 |
n |
Если x ≠ θ , |
то среди компонент вектора |
x |
найдется xi ≠ 0 , |
1 ≤ i ≤ n , тогда x2 |
+...+ x2 > 0 и (x, x) > 0 , следовательно, аксиома IV |
||
1 |
n |
|
|
выполняется.
Таким образом, линейное пространство арифметических векторов
Rn со скалярным произведением (8.2) является евклидовым пространством.
В любом евклидовом пространстве En справедливы следствия из аксиом I - IV:
а) x En (x,θ) = 0 ; |
|
б) если x = α1a1 +... +αk ak , |
y = β1b1 +... +βlbl , то |
k |
l |
(x, y) = ∑∑αiβj (ai ,bj ). i=1 j=1
Доказательство следствий проведите самостоятельно.

Определение 2. Нормой вектора x En называется число, равное
(x, x) .
Обозначим норму: 
 x
x
 . Норма
. Норма 
 x
x
 - аналог длины вектора,
- аналог длины вектора,
определенной для геометрических векторов.
Угол между векторами x и y в евклидовом пространстве определяется равенством
|
|
|
|
|
|
|
|
|
|
|
|
|
(x,y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
cos |
x,y |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
(8.3) |
|||||||||||||||||||||||
|
|
|
x |
|
|
|
y |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Покажем, что угол |
|
|
действительно |
|
|
|
можно определить |
|||||||||||||||||||||||||||||||||||||||||||
x,y |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
равенством (8.3), то есть покажем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
(x,y) |
|
≤1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Теорема 1 (неравенство |
Коши - Буняковского). Для любого |
|||||||||||||||||||||||||||||||||||||||||||||||||
x En и любого y En справедливо неравенство |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
(x, y)2 ≤ |
|
|
|
x |
|
|
|
2 |
|
|
|
y |
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
(8.4) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Доказательство. Пусть |
α - |
произвольное вещественное число. |
||||||||||||||||||||||||||||||||||||||||||||||||
Положим a = x −αy . Тогда по аксиоме IV имеем |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
(a,a) = (x −αy,x −αy) ≥ 0 . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Воспользуемся аксиомами I - III: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
f (α) = (x −αy, x −αy) = (x,x) −2α(x, y) +α2 (y, y) ≥ 0 . |
||||||||||||||||||||||||||||||||||||||||||||||||||
Так как α f (α) ≥ 0 , |
то дискриминант D |
|
|
|
квадратного трехчлена |
|||||||||||||||||||||||||||||||||||||||||||||
f (α) неположителен: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = 4(x, y)2 −4(x, x)(y, y) ≤ 0 . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Отсюда (x, y)2 ≤ (x,x)(y, y) |
|
|
или |
(x, y)2 ≤ |
|
|
|
x |
|
|
|
2 |
|
|
|
y |
|
|
|
2 , и неравенство |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
(8.4) выполняется. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Упражнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Пусть x = (x1, x2 ) и |
y = ( y1, y2 ) - |
произвольные векторы |
пространства арифметических векторов R2 . |
Показать, что скалярное |
|
произведение в R2 можно определить следующими способами: |
||
а) (x, y) = 2x1 y1 +5x2 y2 ; |
б) (x, y) = x1 y1 +3x2 y2 . |
|
Вычислить скалярное произведение векторов x = (1, −2) и y = (5,1)
каждым из указанных способов.
2. Доказать, что в пространстве C[a,b] соотношение
b
( f , g) = ∫ f (x)g(x)dx
a
задает скалярное произведение. Написать неравенство Коши - Буняковского для этого пространства.
8.2. Ортогональные и ортонормированные базисы в En
Определение 3. Пусть En - евклидово пространство, x En , y En . Векторы x и y называются ортогональными, если
(x, y) = 0 .
Определение 4. Система векторов a1,a2 ,...,ak называется ортогональной системой векторов в евклидовом пространстве En ,
если (ai ,a j ) = 0 при i ≠ j, i, j =1,.., k .
Справедливо следующее утверждение. |
|
|
|
Теорема 2. В евклидовом пространстве En |
всякая |
система |
|
ненулевых попарно ортогональных векторов линейно независима. |
|||
Доказательство. Пусть a1,a2 ,...,ak |
- произвольная ортогональная |
||
система векторов в En ; i =1,.., k ai ≠ θ . |
|
|
|
Пусть |
|
|
|
α1a1 +... +αk ak |
= θ. |
|
(8.5) |
Умножим обе части (8.5) скалярно на a1 : |
|
|
|
α1(a1,a1) +α2 (a2 ,a1) +... +αk (ak ,a1) = (θ,a1) . |
(8.6) |
||
Поскольку система векторов a1,a2 ,...,ak ортогональна, |
то верны |
||
равенства: (a2 ,a1) = 0 ,…, (ak ,a1) = 0 ; следствие а) |
из аксиом дает |
||
(θ,a1) = 0 ; согласно аксиоме IV (a1,a1) > 0 . Тогда из равенства (8.6)
получим α1 = 0 .
Аналогично, скалярно умножая (8.5) последовательно на a2 ,...,ak , получим α2 =... = αk = 0 , следовательно, система a1,a2 ,...,ak - линейно
независима.
Теорема доказана.
Опишем процесс построения ортогонального базиса в линейной оболочке любых k линейно независимых векторов.
Пусть a1,a2 ,...,ak - линейно независимы. Шаг 1. Примем b1 = a1 .
Шаг 2. Примем b2 = α1b1 +a2 . Отметим, что b2 ≠ θ, так как b2 является линейной комбинацией a1 и a2 , причем a1 и a2 линейно
независимы (линейная комбинация векторов a1 и a2 с
коэффициентами, один из которых, |
а именно коэффициент при a2 , |
|||||||||||||
заведомо отличен от нуля, не может равняться нулю). |
||||||||||||||
Подберем α1 так, чтобы (b1,b2 ) = 0 , то есть |
|
|
|
|||||||||||
(α b +a |
2 |
,b ) = α (b ,b ) +(a |
2 |
,b ) = 0 и α |
|
= − |
(a2 ,b1) |
. |
||||||
|
|
|||||||||||||
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
b1 |
≠θ (b1,b1) |
||||
|
|
|
|
|
|
|
|
|
|
|
(b1,b1)≠0 |
|||
Шаг |
3. |
Примем b3 = β1b1 +β2b2 +a3 . Отметим, что b3 ≠ θ , так |
||||||||||||
как b3 является линейной комбинацией a1 , a2 и a3 , а эти векторы
линейно независимы. Подберем β1 |
|
и |
β2 |
так, |
|
чтобы |
(b3,b1) = 0 и |
||||||||||||||||||||||||||||
(b3,b2 ) = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(b3,b1) = (β1b1 +β2b2 +a3 ,b1) =β1(b1,b1)+β2 (b2 ,b1)+(a3,b1) = 0, |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≠0 |
|
|
|
|
|
=0 |
|
|
|
|
|
|
|
|||
(b |
3 |
,b |
2 |
) = |
(β b |
+β |
2 |
b |
2 |
+a |
3 |
,b |
2 |
) =β |
(b |
,b |
2 |
)+β |
2 |
(b |
2 |
,b |
2 |
)+(a |
3 |
,b |
2 |
) = 0, |
|||||||
|
|
|
1 |
1 |
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=0 |
|
|
|
|
|
|
≠0 |
|
|
|
|
|
|
|
||
отсюда |
|
|
|
|
|
|
|
|
|
(a3,b1) |
|
|
|
|
(a3,b2 ) |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
β = − |
, β |
2 |
= − |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
(b1,b1) |
|
|
(b2 ,b2 ) |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Шаг |
4. Пусть уже построена ортогональная система ненулевых |
||||||||||||
векторов |
b1,...,bs , |
причем i, 1 ≤ i ≤ s , |
bi |
является |
линейной |
||||||||
комбинацией векторов a1,...,ai . |
|
|
|
|
|
|
|
|
|
||||
Положим |
bs+1 = γ1b1 +... +γsbs +as+1 . |
|
|
|
|
||||||||
Вектор bs+1 ≠ θ, |
|
|
|
|
|||||||||
так как является линейной комбинацией линейно |
|||||||||||||
независимых векторов |
a1,a2 ,...,as+1 |
с коэффициентами, |
один |
из |
|||||||||
которых, |
а именно коэффициент при as+1 , |
заведомо отличен от нуля |
|||||||||||
(поскольку as+1 не входит в b1,...,bs ). |
|
|
|
|
|
|
|||||||
Коэффициенты γ1,..., γs подберем так, чтобы bs+1 был |
|||||||||||||
ортогонален векторам b1,...,bs : |
|
|
|
|
|
|
|
|
|
||||
Отсюда |
(bs+1,bi ) = 0, |
i =1, 2,..., s . |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(bs+1,bi ) = (γ1b1 +... +γsbs +as+1,bi ) = γ1 (b1,bi )+... + |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
=0 |
|
|
|
|
+γi (bi ,bi )+... +γs (bs ,bi )+(as+1,bi ) = 0 |
|
|
|
|||||||||
и |
|
≠0 |
|
|
=0 |
|
|
|
|
|
|
||
|
|
|
(as+1 |
,bi ) |
|
|
|
|
|
|
|
||
|
|
γi |
= − |
, |
i =1,..., s . |
|
|
|
|
||||
|
|
(bi ,bi ) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Продолжая процесс, построим ортогональную систему векторов |
|||||||||||||
b1,...,bk , |
причем i, i =1,..., k , |
bi |
|
≠ θ , откуда |
в силу теоремы |
2 |
|||||||
следует, что b1,...,bk |
- линейно независимы. Линейная оболочка |
L |
|||||||||||
векторов |
a1,...,ak |
является |
|
подпространством |
размерности |
||||||||
k ( dim L = k ), а это означает, что b1,...,bk - базис в L |
(по построению |
||||||||||||
- ортогональный).
Описанный выше процесс носит название процесса
ортогонализации Шмидта.
Пример 3. E3 - евклидово пространство геометрических векторов. Применяя процесс ортогонализации Шмидта, построить ортогональный базис в подпространстве, натянутом на векторы a1 = (1, 2, 2) и a2 = (−1,1, −5) .
Полагаем
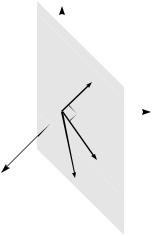
b1 = a1 = (1, 2, 2) , b2 = α1b1 +a2 .
Подбираем α1 :
(b2 ,b1) = (α1b1 +a2 ,b1) = = α1(b1,b1) +(a2 ,b1) = 0 , |
|
||||||||||||
|
|
z |
откуда α |
= − |
(a2 ,b1) |
|
= − −1+2 −10 =1 . |
||||||
|
|
|
|||||||||||
|
|
|
|
1 |
|
(b1,b1) |
|
1+ 4 +4 |
|
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Итак, |
b2 = b1 +a2 ={0,3, −3}, |
и |
|||||||
|
|
a1 (b1) |
базис в линейной |
оболочке |
L(a1,a2 ) |
||||||||
|
|
составляют |
векторы |
b1 = (1, 2, 2) , |
|||||||||
|
|
|
|
||||||||||
O |
|
|
|
b2 = (0,3, −3) . |
|
|
|
|
|
|
|
||
|
y |
Геометрический |
смысл |
процедуры |
|||||||||
|
|
b2 |
иллюстрирует рис. 8.1. Подпространство |
||||||||||
|
|
L , натянутое на |
|
|
вектора |
a1,a2 , |
- |
||||||
x |
a2 |
|
|
||||||||||
плоскость, проходящая через O(0, 0, 0) |
и |
||||||||||||
|
|
||||||||||||
|
|
|
|
векторы a1 и a2 , приведенные к точке |
|||||||||
|
|
|
|
O(0, 0, 0) . В этой плоскости построен |
|||||||||
Рис. 8.1. |
базис b1 , b2 , |
такой, что b1 b2 . |
|
||||||||||
Упражнения. |
|
|
|
|
|
|
a1 = (1, −2,1,3) |
|
|||||
1. Проверить ортогональность системы векторов |
и |
||||||||||||
a2 = (2,1, −3,1) |
в евклидовом |
пространстве |
R4 |
и |
дополнить ее |
до |
|||||||
ортогонального базиса. |
|
|
|
|
|
|
|
|
|
||||
2.Применяя процесс ортогонализации Шмидта, построить
ортогональный базис |
в |
линейной |
оболочке |
системы |
векторов: |
|
f1 = (1, −2, 2) , f2 = (−1,0, −1) , f3 = (5, −3, −7) , f4 = (6, −5, −5) . |
|
|||||
Замечание. |
Всякое |
евклидово |
пространство En |
обладает |
||
ортогональными базисами. |
En - евклидово пространство, dim En = n , |
|||||
Действительно, |
пусть |
|||||
e1,e2 ,...,en - базис |
в |
En . |
Применим |
к базису |
e1,e2 ,...,en |
процесс |
ортогонализации Шмидта - получим некоторый ортогональный базис в
En .
Определение 5. Вектор a, a En называется нормированным, если 
 a
a
 =1 .
=1 .
|
|
|
|
Если |
a ≠ θ, |
то |
нормированием называется |
переход |
|
к |
вектору |
|||||||||||||
b = |
|
a |
( b |
|
|
|
|
|
|
|
|
|
|
(b,b) = |
|
|
a |
, |
|
a |
|
|
||
|
|
является |
нормированным, так |
как |
|
|
|
|
|
|
= |
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|
|
= |
1 |
|
(a,a) =1 и, следовательно, |
|
b |
|
=1 ). |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
a |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Определение |
6. |
Система |
векторов |
e1,e2 ,...,ek в |
евклидовом |
|||||||||||||||
пространстве En |
называется ортонормированной системой, если |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
1, |
если |
|
i = j |
, |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
(ei ,e j ) = |
если |
|
i ≠ j, |
i, j =1,...k. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|||||||
Всякое евклидово пространство обладает ортонормированными базисами.
В самом деле, ранее было показано, что всякое евклидово пространство обладает ортогональными базисами. Возьмем в En
произвольный ортогональный базис b1,...,bn и нормируем все его векторы, то есть перейдем к системе векторов
e |
= |
|
b1 |
,...,e |
n |
= |
|
bn |
. |
(8.7) |
|
|
|
|
|||||||
1 |
|
|
b1 |
|
|
|
bn |
|
|
Система (8.7) - ортонормированный базис в En .
Пример 4. E3 - евклидово пространство геометрических векторов. Указать какой-нибудь ортонормированный базис в линейной
оболочке векторов a1 = (1, 2, 2) и a2 = (−1,1, −5) . |
|
|
|
|
|
|
|||||||||||||||||
В примере 3 был построен |
ортогональный |
базис |
|||||||||||||||||||||
b2 = (0,3, −3) в L(a1,a2 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Имеем |
|
|
|
b1 |
|
1 |
|
2 |
|
2 |
|
||||||||||||
|
|
|
|
b |
|
|
|
= 1+4 + 4 = 3 , |
e |
= |
|
= |
, |
, |
, |
||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
|
b1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
3 |
|
|||||
|
b2 |
|
= 0 +9 +9 = 18 = 3 2 , |
e2 = |
|
b2 |
|
= |
|
0, |
1 |
, − |
|||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
b2 |
|
2 |
||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
b1 = (1, 2, 2) ,
1
. 2
Векторы e1,e2 - ортонормированный базис в L(a1,a2 ) .
Упражнения.
1. Указать какой-нибудь ортонормированный базис в линейной оболочке векторов f1 = (1, −2, 2) , f2 = (−1,0, −1) , f3 = (5, −3, −7) ,
f4 = (6, −5, −5) .
2.E3 - евклидово пространство геометрических векторов. Построить какой-нибудь ортонормированный базис в линейной
оболочке векторов a1 = (1,1,1) , a2 = (1, 2,3) и a3 = (2,1,0) .
