Казанский государственный технический университет

им А.Н. Туполева

Заботин В.И., Дуллиев А.М., Черняев Ю.А.

МАТЕМАТИЧЕСКИЙ АНАЛИЗ ЧАСТЬ 1

Казань - 2005

ГЛАВА 1. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ.

1.1Множества, функции, логические символы.

Всюду в нашем курсе понятия элемента множества, множества и принадлежности элемента множеству будут считаться первичными понятиями, т.е. такими понятиями, которые не определяются с помощью других, ранее введенных определений. Такая точка зрения на множества и их элементы (принадлежащая немецкому математику Г. Кантору) не является единственной, но этот вопрос в данном курсе лекций обсуждаться не будет.

Итак, мы будем основываться, на интуитивном представлении о множестве и его элементах полагая, что представление одинаково у всех, кто будет читать нижеследующий материал.

Множества мы будем обозначать большими буквами латинского алфавита: A, B, C,... , а элементы множеств – малыми буквами: Часто будут использоваться и буквы греческого алфавита (приведем наиболее употребляемые):

α− называется альфа; произносится «а»

β──────бета; ──────── «б»

γ──────гамма; ──────── «г»

δ ──────дельта; ──────── «д»

ε──────эпсилон; ────── «е» (краткое)

ς──────дзета;──────── «дз»

η──────эта; ──────── «е»(долгое)

ϑ──────тета; ──────── «т»

κ──────каппа;──────── «к»

λ───── ламбда; ──────── «л» μ ──────ми; ──────── «м»

ν ──────ни;──────── «н»

ξ──────кси; ──────── «к»

π──────пи;──────── «п» ρ ──────ро; ──────── «р»

σ ──────сигма; ──────── «с» τ ──────тау;──────── «т»

υ──────ипсилон; ──────── «и»

φ──────фи; ──────── «ф»

χ ──────хи; ──────── «х» ψ ──────пси;──────── «пс»

ω──────омега;──────── «о» (долгое)

Вразговорном русском языке часто μ называют «мю», а ν – «ню».

5

Если a является элементом A , то пишут a A и говорят: « a принадлежит множеству A ». Если a не является элементом A , то пишут a A (говорят «a не принадлежит множеству A »).

Если из того, что a A следует, что a B , то говорят, что A является подмножеством B или, что A включается в B , и обозначают: A B . Если A B и B A , то говорят, что множества A и B равны и обозначают так: A = B . Другими словами, равенство двух множеств означает, что одно и то же множество обозначено двумя разными буквами. Если A и B не равны (то есть в одном из них есть элемент, не принадлежащий другому), то пишут:

Если и A ≠ B , то A называют собственным подмножеством

B , или частью B .

Для обозначения множеств мы зарезервируем скобки {…} и в этом курсе не будем их использовать ни для каких иных целей.

А именно: через {a} будем обозначать множество, состоящее из одного элемента a . Здесь сразу заметим, что нельзя путать {a} и a ,– одноэле-

ментное множество и элемент,– у них разная природа. Ниже мы еще вернемся к этому разговору.

Запись A ={a, b, c,..., k} означает, что задано множество из конечного числа элементов, которые перечислены в скобках, например, запись A ={1, 2, 3,..., 11} означает, что A состоит из натуральных чисел от 1 до 11.

Ясно, что указанная запись удобна в случаях, когда множество состоит из конечного числа элементов.

Очень часто множество A состоит из элементов x , обладающих некоторым определенным свойством p (x) (свойство p (x) является неким пра-

вилом построения A ). В этом случае будем применять запись

A ={x: p (x)} или A ={x| p (x)}.

Часто, если заранее известно, что x берутся из заранее заданного множества M, то применяется и такая запись:

A ={x M : p (x)} или A ={x M | p (x)} ;

читается это так: «Множество A состоит из элементов множества M таких, что выполняется свойство p (x) ».

Например: если, как и раньше, через R будем обозначать числовую прямую, то запись

A ={x R:a ≤ x ≤b}

означает, что множество A – это отрезок [a, b] , а запись

A ={x R:x > 0}

означает, что A = R+ – положительная полупрямая.

В дальнейшем нам будет удобно рассматривать так называемое пустое множество . По определению, пустым назовем множество, в котором нет элементов. Например,

6

= {x R : x > 0 и x < −1} .

Заметим, что элементами множества в свою очередь могут являться множества, например запись

A = {{a}, {a, b}, {a, b, c}}

говорит о том, что элементами A является одно, двух и трехэлементное множества.

В связи со сказанным мы можем рассмотреть множество { }, которое не будет пустым! В нем есть один элемент – пустое множество. Вот еще одно подтверждение тому, что нельзя путать два понятия: множество и элемент множества.

Введем теперь в рассмотрение так называемые логические символы. В математических рассуждениях постоянно приходится иметь дело с

выражениями «существует элемент такой, что…», «для любого элемента из множества A …». Более того, такие выражения в определенном смысле дополняют друг друга. Действительно, если мы хотим сказать, что не существует элемента с некоторым заданным свойством, то мы скажем, что для любого элемента это свойство невозможно. И наоборот, если мы хотим сказать, что не для любого элемента имеет место свойство P , то скажем так: существует элемент, для которого P не выполняется.

Важность для математики выражений «для любого…» и «существует…» трудно переоценить. Если мы хотим объяснить, что A состоит из чет-

В связи со сказанным введем следующие символы: вместо слов «любой», «для любого», «каждый» и т.п. будем употреблять символ , называемый «квантор всеобщности», а вместо слов «существует», «найдется» и т. п. – символ , называемый «квантор существования». ( – перевернутая первая буква слова «All», – перевернутая первая буква слова «Existence»)

Например: предложение «для любого числа x найдется число y ,

большее, чем x » можно теперь записать так:

( x R) ( y R) : x < y .

Здесь появился еще один символ – двоеточие. Этот символ (и равносильный ему символ | – прямая вертикальная черта) здесь и всюду далее мы будем читать так: «такой, что имеет место», «имеет место». В указанной за-

писи можно скобки отбрасывать и писать так:

x R y R : x < y .

Очень важно понять, что в этой записи выбор y зависит от того, какой был задан x . В предложении: «для любой головы найдется шляпа, ко-

7

торая на эту голову наденется», – выбор этой шляпы зависит от величины головы. Высказывание имеет совсем другой смысл!

Мы будем также использовать знак и читать его: «следует». Знак(или равносильный ему ≡) будет означать тождественность высказываний, стоящих по обе стороны от данного знака и читаться «тогда и только тогда», «если и только если» и т. п.

Например: если мы хотим сказать, что A не является подмножеством

B (запись: A B ), то можно записать следующее тождество:

A B x A : x B .

Знак будет означать отрицание высказывания. Для нас он также будет иметь большее значение, поскольку часто для доказательства теорем от противного нужно суметь построить отрицание так, чтобы оно читалось как

R такой, что x меньше y », смысл полученного высказывания очень трудно понять. Попробуем облегчить его понимание, для этого заметим, что если «не для любого x имеет место P(x) », то это равносильно тому, что «суще-

ствует x , для которого P(x) не выполняется». В нашем примере это выглядит так:

x R ( y R : x < y) .

Теперь следующим шагом надо понять значение полученного отрица-

ния ( y R : x < y) . Но это уже легче: y R : ( x < y) . И окончательноx R y R : x ≥ y .

Мы получили отрицание высказывания (1.1).

Пример 2. Вспомним определение периодической функции и запишем его с помощью символики:

T >0 x R : f (x +T ) = f (x) .

Как записать теперь тот факт, что f – непериодична? Рассуждая, как и выше сначала получим такое высказывание:

T > 0 ( x R : f (x +T ) = f (x)) .

После чего:

T >0 x R : ( f (x +T) = f (x)) .

Наконец:

T > 0 x R : f (x +T ) ≠ f (x) .

8

Из этих примеров видим, что знак отрицания «проходя сквозь высказывания» заменяет квантор существования на квантор всеобщности и наоборот. Этим правилом мы будем часто пользоваться в дальнейшем.

Знаки и будут нам заменять союзы «и» и «или». При этом не является исключающим типа «или…или…», т.е., если мы запишем

(x A) (x B) ,

то это означает, что x по крайней мере, находится в одном из указанных множеств, но может находиться и в обоих сразу.

В курсе школьной математики уже были введены понятия пересечения и объединения множеств.

1. Пересечение.

Пересечение двух множеств A и B есть множество:

A ∩B ={x | x A x B} ,

то есть A ∩ B состоит из тех и только тех элементов, которые принадлежат и А и В одновременно.

2. Объединение.

Объединение двух множеств А и В есть множество

A B ={x | x A x B} ,

то есть A B состоит из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А и В.

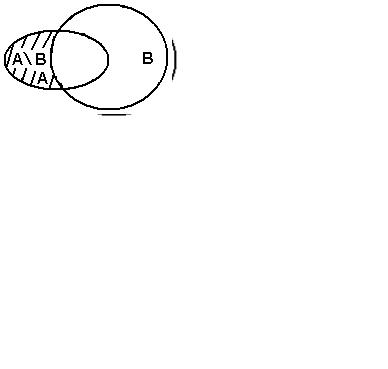
Сказанное можно проиллюстрировать с помощью рисунков:

Вопрос: что значит A ∩ B = ? A B = ? 3. Разность.

Разностью множеств А и В называется множество

A \ B ={x | x A x B} .

Часто объединение, пересечение и разность называют теоретикомножественными операциями. Действительно – на A B , например, можно смотреть как на операцию над двумя множествами А и В, в результате которой получено третье множество, обозначаемое A B .

9

Три введенные операции можно считать основными. С их помощью вводятся еще две операции.

4. Дополнение. Обозначим Х некоторое множество, которое назовем «основным», и которое содержит все остальные множества, которые мы в данный момент рассматриваем. Например, если мы работаем с числовыми

множествами, то Х=R – вся числовая прямая; если мы рассматриваем множества двумерных векторов, то Х – координатная плоскость и т. д.

В этом случае для A X обозначим

CA = X \ A .

И будем CA называть дополнением A :

5.Симметрическая разность.

Для двух множеств А и В обозначим

AB = ( A B) \ ( A ∩ B) .

Иназовем это множество симметрической разностью множеств A и В:

заштрихованная часть рисунка, – это и есть симметрическая разность. Правила действия над множествами.

1. Для любого множества A всегда A.

Доказательство. Предположим противное: A. Но это означает, что в есть элементы, не принадлежащие A , чего быть не может, т. к. в

элементов нет. Полученное противоречие доказывает теорему.

2.A A . (Это свойство называется рефлексивностью включения.)

Доказательство очевидно: если x A, то x A.

3. ( A B) (B D) A D . (Это свойство называется транзи-

тивностью включения.)

Доказательство очевидно: если x A, то x B , но если x B , то x D , то есть x A x D что и требовалось доказать.

4. Для любых A , B справедливо: A B = B A; A ∩ B = B ∩ A. (Эти свойства объединения и пересечения называются коммутативно-

стью.)

10