
Zabotin_Dulliev_Chernyaev_-_Mat_an
.pdf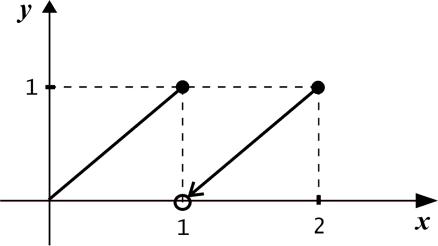
Пользуясь вновь леммой 1.5.5, выделим |
xn |
→ x0 [ a ; b ] . Выделим |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
k |
|
|
|
|
|
|
|||||||
теперь подпоследовательность |
yn |
k |
|
(с теми же номерами) и покажем, что |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
→ x |
|
|
|
y |
− x |
|
|
|
|
|
|
|
y |
|
− x |
|
|
|
x |
|
− x |
|
|
|
1 |
+ |
|
|
|
x |
− x |
|
→0 |
|
|||||||||||
0 : |
|
0 |
|
≤ |
|
n k |
|
+ |
|
0 |
< |
|
|
0 |
, по- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
n k |
|
|
|
n k |
|
|
|
|
|
|
|
n k |
|
|
|
|
|
n k |
|
|
|
nk |
|
|
|
|
n k |
k |
|
|
|||||||||||||||
скольку |
|
x |
n k |
|
→ x |
0 . Но тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (xn |
k |
) − f ( yn |
) |
|
≥ε . |
|
|
|
|
|
|
|
|
|
|
(1.5.4) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку y = |
|
x |
|
|
есть, очевидно, непрерывная функция, то |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
f (xn |
|
) − f ( yn |
|
|
|
|
lim f (xn |
|
|
f ( yn |
|
|
|
f (x0 ) − f (x0 ) |
|
|
||||||||||||||||||||||||||||
|
lim |
|
|
|
) |
|
= |
|
) − lim |
) |
= |
|
|
= 0 , |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
k |
|
|
|
|
k |
|
|
|
|
|
k |
|
|
|
|
|
|
|
k |
|
|
|
|
k |
|
|
k |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
||
чего в силу (1.5.4) быть не может. Полученное противоречие доказывает теорему.
Теперь приступим к изучению связей между такими свойствами функций, как непрерывность и монотонность, поскольку монотонные функции представляют собой класс функций, обладающих специфическими, «хорошими», свойствами. Так, например, мы видели, что всякая непрерывная функция принимает на отрезке любое из значений, заключённых между наибольшим и наименьшим значениями f . Обратное утвер-
ждение, однако, далеко не всегда справедливо: если мы рассмотрим функцию
x, x [0;1]; f (x) =
x −1, x (0; 2],
график которой имеет вид:
то она, будучи разрывной, тем не менее принимает любое значение между f (0) =0 и f (2) =1. Но если от f потребовать монотонности, то картина
меняется.
81

Теорема 1.5.9. Если f монотонна на отрезке [a; b] и принимает
любое значение между наибольшим и наименьшим, то она непрерывна на
[a; b] .
Доказательство. Положим для определённости, что f монотонно
возрастает, т. е. x1 <x2 f (x1 ) ≤ f (x2 ) . Тогда f (a) – её наименьшее, а f (b)
– наибольшее значения на [a; b] , т. е. f ограничена на [a; b] .
Пусть x0 [a; b], тогда, в силу монотонности и ограниченности, су-
ществуют lim f (x) =c1 |
и lim f (x) =c2 . Очевидно, c1 ≤ f (x0 )≤c2 . Строгое не- |
|
x↑x0 |
x↓x0 |
|
равенство c1 < f (x0 ) |
невозможно, иначе ни |
одно из чисел интервала |
(c1 ; f (x0 ) ) не может быть значением f , т. е. c1 = f (x0 ) . По той же причине |
||
c2 = f (x0 ) . |
f непрерывна в точке x0 |
как слева, так и справа, что |
Таким образом, |
||
и требовалось. |
|
|
Теорема 1.5.10. Если f строго монотонна на [a; b] , то у неё существует обратная функция, также строго монотонная. Если, кроме того,
f непрерывна на [a; b] , |
то областью определения обратной функции яв- |
||||||||||
ляется отрезок и она непрерывна на нём. |
|
f строго возрастает, то |
|||||||||
|
Доказательство. Пусть для определённости |
||||||||||
есть |
x1 <x2 f (x1 ) < f (x2 ) . Но это значит, что x1 ≠x2 f (x1 ) ≠ f (x2 ) и |
f |
|||||||||
обратима (инъективна). Если же y1 |
и y2 – значения |
f |
такие, что y1 < y2 , то |
||||||||
x1 = f −1 ( y1 )<x2 = f −1 ( y2 ) |
(в |
противном |
случае, |
если x1 ≥x2 , |
то |
||||||
f (x1 ) = y1 ≥ f (x2 ) = y2 , |
чего нет). Таким образом, обратная функция также |
||||||||||
строго возрастает. |
|
|
|
|
|
|
|
|
|
||
|
Если же f |
непрерывна, |
то она принимает любое значение между |
||||||||
f (a) |
и f (b) , |
т. |
е. |
областью |
определения |
f −1 |
является |
отрезок |
|||
[ f (a); f (b) ]. Наконец, для любого x [a; b] |
определено значение |
y = f (x) |
|||||||||
и f −1 ( y) =x , т. е. обратная функция принимает любое значение x [a; b] , откуда следует её непрерывность. Теорема доказана.
Непрерывность элементарных функций.
Напомним, что к элементарным функциям мы относим степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические функции.
Непрерывность тригонометрических и обратных тригонометрических функций на их области определения почти очевидна. Например, если f (x) =sin x , то
|
|
|
|
x |
|
|
x |
|
|
x |
|
|
|
| x | |
|
||
f (x0 + |
x) − f (x0 ) |
= 2 |
sin |
|
cos x0 |
+ |
|
|
≤ 2 |
sin |
|
|
≤ 2 |
|
|
=| x | , |
|
2 |
2 |
2 |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
82
откуда следует, что для любого ε>0 достаточно взять δ=ε, чтобы выпол-
нилось определение непрерывности в точке x0 |
на языке Коши. А посколь- |
||||||
ку |
f (x) =sin x строго монотонна на отрезке |
|
π |
, |
π |
, то arcsin x |
непрерыв- |
− |
2 |
|
|||||
|
|
|
|
2 |
|
|
|
на и строго монотонна на [−1;1] .
Гораздо сложнее дело обстоит с показательными и степенными функциями. Дело в том, что в школьном курсе математики нет определения того, чтό понимать, например, под функцией y =ax , a >0, a ≠1, если х –
любое действительное число. Точнее, как понимать значение ax , если х – иррациональное число. Отметим здесь, что если х – иррациональное число, то оно может быть представлено как предел последовательности рацио-
нальных чисел: x =lim rn . Поскольку возводить число в рациональную сте-
n
пень мы умеем, то по определению будем полагать ax =lim arn .
n
Разумеется, нужно показать, что, во-первых, этот предел существует и, во-вторых, что он не зависит от выбора последовательности rn , сходящейся к х. После этого уже можно доказать строгую монотонность и непрерывность y =ax , а потом легко исследовать и непрерывность loga x .
Для того чтобы строго реализовать этот путь, потребуется достаточно много работы, поэтому мы без доказательства примем тот факт, что все элементарные функции непрерывны в любой точки области их определения.
Подробно о непрерывности элементарных функций можно прочитать в любом достаточно полном учебнике по математическому анализу, например, в книгах [1], [2].
83
Упражнение 1.5. |
|
|
|
|
|
|
|
|
|
|
|
|
||
1. Показать, что при x = 5 |
функция f (x) = |
x2 |
−25 |
имеет разрыв. |
||||||||||
x |
−5 |
|
||||||||||||
|
|
x = 5 |
|
|
|
|
|
|
|
|||||
Решение. В точке |
функция не определена. В других точках |
|||||||||||||
дробь можно сократить на |
x −5 . |
Следовательно, |
|
f (x) = x +5 при |
||||||||||
x ≠ 5 . Легко видеть, что |
lim f (x) = lim f (x) =10. Таким образом, |
|||||||||||||
|
|
|
x→5−0 |
x→5+0 |
|
|
|
|
|
|
||||
при x = 5 функция имеет устранимый разрыв. |
|
|
|
|
||||||||||
2. Показать, что при x = 4 функция f (x) = arctg |
1 |
|
имеет разрыв. |
|||||||||||
x − |
4 |
|||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
||||
Решение. Если x → 4 −0 , |
то |
|
→−∞ и |
lim |
f (x) = −π / 2 . Если же |
|||||||||
|
x −4 |
|||||||||||||
|
1 |
|
|
|
|
x→4−0 |
|
|
|
|
||||
x →4 +0 , то |
→+∞ |
и |
|
lim |
f (x) =π / 2 . |
Итак, при при x →4 |
||||||||
x −4 |
|
|||||||||||||
|
|
|
|
x→4+0 |
|
|
|
|
|
|
|
|||
имеет как левый, так и правый конечные пределы, причём они различны. Следовательно, x = 4 является точкой разрыва I рода – точкой скачка. Скачок функции в этой точке равен π .
3. Показать, что при x = 4 функция |
f (x) = |
|
x |
имеет разрыв. |
|
|
x −4 |
||||
|
lim f (x) = −∞, |
|
|
|
|
Решение. Находим |
lim |
f (x) =+∞. Таким образом |
|||
|
x→4−0 |
x→4+0 |
|
|
|
функция при x = 4 не имеет ни левого, ни правого конечного пределов. Следовательно, x = 4 является точкой разрыва II рода.
4. Найти точки разрыва функций и определить характер разрыва:
21/(x−2) −1 а) f (x) = 21/(x−2) +1 ;
б) |
f (x) = |
|
|
|
1 |
|
|
|
; |
|
|
|
||||
|
(x −1)(x −5) |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||
в) |
f (x) = |
|
|
|
1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
1−x |
|
|
|
|
|
|
|
||||||
|
|
1−e |
|
1 |
|
|
|
|
|
|||||||
|
|
t g xarctg |
|
|
|
|
|
|
||||||||
г) f (x) = |
x |
−3 |
; |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x(x −5) |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
д) |
f (x) = |
|
|
|
|
x +1 |
|
|
|
|
|
; |
||||
x3 |
+6x2 +11x + |
6 |
||||||||||||||
|
|
|
||||||||||||||
е) |
f (x) = |
1 |
ln |
1+ x |
; |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
x |
1− x |
|
|
|
|
|
|
|
||||||
84
|
|
|
|
1 |
− |
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
x +1 |
|
|
|
||||||||
ж) |
f (x) = |
x |
; |
|
||||||||||||
|
|
|
|
|
|
|||||||||||
|
|
1 |
|
|
|
− |
1 |
|
|
|
|
|||||
|
|
|
|
x −1 |
x |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
з) f (x) = |
1−cosx |
|
; |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
||
и)* |
f (x) =[x] (наибольшее целое не превосходящее x); |
|||||||||||||||
к)* f (x) ={x} (=[x] − x ); |
||||||||||||||||
|
|
|
|
1 |
, x |
= |
|
m |
−несократимая дробь, |
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
n |
||||||||||
л)* |
f (x) = n |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0, x −иррационально или x = 0. |
||||||||||||
5. Доказать, что если в определении предела функции f в точке x0 (в смысле Коши или Гейне) отбросить условие x ≠ x0 , то мы получим определение непрерывности функции f в точке x0 .
6*. Доказать, что если функции f и g непрерывны, то и функции max{f , g} и min{f , g} также непрерывны.
7*. Показать, что для функции f , непрерывной на [a,b], и любых точек x1 , x2 ,...,xn из [a,b], существует такая точка x0 [a,b], в которой
f (x0 ) = |
f (x1 ) + f (x2 ) +... + f (xn ) |
. |
|
||
|
n |
|
8. Исследовать на равномерную непрерывность на заданных множествах:
а) |
f (x) = ln x , |
D = (0; 1] ; |
|
||||
б) |
f (x) = |
sin x |
, |
D = (0; π] ; |
|
||
x |
|
||||||
|
|
|
1 |
|
|
||
в) |
f (x) = ex cos |
, D = (0; 1] |
; |
||||
|
|||||||
|
|
|
|
x |
|
||
г) |
f (x) = arctgx , D = R ; |
|
|||||
д) |
f (x) = x , |
D =[0; +∞) ; |
|
||||
е) |
f (x) = xsin x , D =[0; +∞) . |
||||||
Решение. а) Докажем, что функция не является равномерно непрерывной на множестве. Для этого достаточно установить истинность утверждения
ε > 0 δ > 0 x1 , x2 D :| x1 − x2 |< δ | ln x1 −ln x2 |≥ ε.
85
Возьмём, |
|
|
|
|
например, |
x1 =1/ δ |
и |
x2 |
=1/(2δ) . |
Тогда |
|||||||||
|
ln |
1 |
−ln |
1 |
|
|
= |
|
ln |
2δ |
|
|
= ln 2 |
, а значит в качестве ε |
можно выбрать ln2. |
||||
|
|
|
|
||||||||||||||||
|
2δ |
δ |
|||||||||||||||||
|
|
δ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Что и требовалось доказать. |
|
|
|
|
|||||||||||||||
9*. Пусть |
|
|
функция f |
монотонна, |
ограниченна |
и непрерывна на |
|||||||||||||
(a, b) . Будет ли она равномерно непрерывной на |
(a,b) . Свой ответ |
||||||||||||||||||
пояснить. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответы. 4. а) 2 – точка разрыва I рода; б) 1 и 5 – точки разрыва II рода; в) 1 – точки разрыва II рода; г) 3 – точка разрыва I рода, 5 – точка разрыва II рода; д) -2 и -3 – точки разрыва II рода, -1 – точка устранимого разрыва; е) -1 и 1 – точки разрыва II рода, 0 – точка устранимого разрыва; ж) - 1 – точка разрыва II рода, 0 и 1 – точки устранимого разрыва; з) 0 – точка устранимого разрыва; и) Z – множество точек разрыва I рода; к) Z – множество точек разрыва I рода; л) Z\{0} – множество точек разрыва II рода. 8. б) равномерно непрерывна; в) не является равномерно непрерывной; г) равномерно непрерывна; д) не является равномерно непрерывной; е) не является равномерно непрерывной. 9. Да.
86

1.6. Дифференциальное исчисление функций одного переменного.
Рассмотрим несколько задач, приводящих к понятию производной функции в точке.
Задача 1. Пусть вдоль оси S движется прямолинейно некоторая точка и пусть в любой момент времени t мы можем найти её координату s(t) на
оси S (т. е. измерить путь, пройденный от начала движения к моменту t).
Если рассмотреть s =s(t + t) −s(t) |
– путь, пройденный за промежуток |
||
времени [t; t + t] , то отношение |
|
|
|
s = |
s(t + t) −s(t) |
|
|
t |
|
t |
|
представляет собой среднюю скорость точки на временном промежутке [t; t + t] . Ясно, что эта характеристика движения тем точнее, чем короче
временной промежуток.
Если существует конечный предел
s(tt) =v(t) ,
то он называется скоростью точки в момент времени t.
Задача 2. Пусть задан прямолинейный стержень с переменной плотностью материала, из которого он изготовлен; толщиной стержня будем
пренебрегать. Пусть х – точка стержня, |
x – длина куска стержня, M (x) – |
масса куска стержня от начала до точки х. Тогда отношение |
|
M (x) = M (x + x) −M (x) |
|
x |
x |
представляет собой среднюю плотность вещества стержня. Если существует конечный предел
Mx(x) =ρ(x) ,
то этот предел называется плотностью (линейной) стержня в точке х.
Мы видим, что в обеих задачах нам пришлось рассматривать предел
вида
f (x0 + x) − f (x0 ) . x
Рассмотрим его геометрический смысл, который не будет зависеть от физической сущности функции f .
87
Запишем уравнение секущей, проходящей через точки (x0 , f (x0 )) и |
||||
(x0 + x, f (x0 + x)): |
|
|
||
y = f (x0 ) + |
f (x0 + x) − f (x0 ) |
(x −x0 ) . |
(1.6.1) |
|
x |
||||
|
|
|
||
Здесь f (x0 + x) − f (x0 ) – угловой коэффициент секущей. Если существует x
конечный предел |
|
|
|
|
lim |
f (x0 + |
x) − f (x0 ) |
=k , |
(1.6.2) |
|
|
|||
x→0 |
x |
|
||
то, переходя к пределу в (1.6.1), получим уравнение |
|
|||
y = f (x0 ) +k (x −x0 ) . |
(1.6.3) |
|||
Полученное уравнение можно истолковать как уравнение прямой, являющейся «предельным положением» секущей. В школьном курсе эту «предельную прямую» назвали касательной. Конечно, приведённые рассуждения не являются строгими уже потому, что мы не знаем, как понимать стремление одной прямой к другой; кроме того, нам надо строго ввести определение касательной к графику функции.
Из приведённых задач мы видим, что всякий раз при введении таких важнейших характеристик, как мгновенная скорость, плотность вещества (задачи можно было бы приводить всё новые) нам приходится рассматривать предел одного и того же вида (1.6.2). Поэтому займёмся его подробным изучением.
88

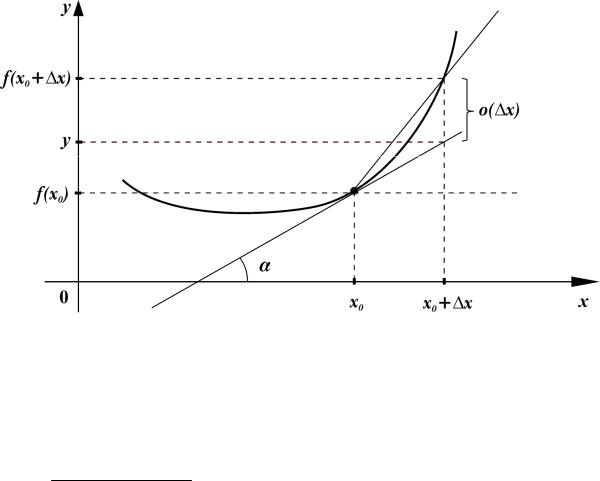
Определение касательной к графику функции.
Пусть хотя бы в окрестности Uδ (x0 ) точки x0 определена функция f . Запишем уравнение прямой, проходящей через точку (x0 , f (x0 )):
y = f (x0 ) +k (x −x0 ) , k – угловой коэффициент.
Эта прямая называется касательной к графику функции f в точке x0 , если для всех x Uδ (x0 ) имеет место (см. рисунок):
f (x) − y = f (x) −( f (x0 ) +k(x −x0 )) =o(x −x0 ) ,
или, что то же самое,
f (x) − f (x0 ) =k (x −x0 ) +o(x −x0 ) .
Поделив обе части равенства на x −x0 , получим:
f (x) − f (x0 ) =k +o(x −x0 ) . |
|
x −x0 |
x −x0 |
Поскольку второе слагаемое в выражении, стоящем справа, имеет предел, равный нулю при x −x0 →0 , то мы видим, что касательная прямая
существует тогда и только тогда, когда существует конечный предел
f (x) − f (x0 ) =k . x −x0
Заметим, что этот предел будет угловым коэффициентом касательной.
Определение производной функции в точке.
Пусть f определена в Uδ (x0 ) и существует конечный предел
|
lim |
|
f (x) − f (x0 ) |
. |
|
|
|
(1.6.4) |
|||||
|
|
|
x −x0 |
|
|
||||||||
|
x→x0 |
|
f в точке x0 и обозначается |
||||||||||
Тогда этот предел называется производной |
|||||||||||||
f / (x0 ) или |
df (x0 ) |
. |
|
|
|
||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
Если положить x −x0 = |
x , то x =x0 + |
x |
и предел (1.6.4) можно за- |
||||||||||
писать так: |
|
|
|
f (x0 + |
x) − f (x0 ) |
|
|
||||||
f / (x0 ) |
= lim |
|
, |
|
|||||||||
|
|
|
|
|
|
|
|||||||
|
x→0 |
x |
|
|
|
|
|
|
|||||
или |
|
|
|
|
|
|
f (x0 ) |
|
|
|
|
||
f / (x0 ) |
= lim |
|
. |
|
|
|
|||||||
|
|
|
|
|
|||||||||
|
|
|
|
x→0 |
x |
|
|
|
|
|
|
||
Таким образом, производная f в точке x0 |
существует тогда и только |
||||||||||||
тогда, когда в этой точке существует касательная к графику |
f . При этом |
||||||||||||
уравнение касательной примет вид: |
|
|
|
|
|
|
|
||||||
y = f (x0 ) + f / (x0 )(x −x0 ) |
(1.6.5) |
||||||||||||
89
и, соответственно, f / (x0 ) есть угловой коэффициент касательной или, что то же самое, f / (x0 ) – тангенс угла наклона касательной в точке (x0 , f (x0 )) . Этот факт называется геометрическим смыслом производной.
|
Если существует |
lim |
f (x0 ) |
и конечен, то его называют левосто- |
|
|
|
||||
|
|
|
x↑0 |
x |
|
ронней производной f |
в точке x0 . Аналогично, если существует конечный |
||||
lim |
f (x0 ) |
, то его называют правосторонней производной f в точке x0 . |
|||
|
|||||
x↓0 |
x |
|
|
|
|
Очевидно, производная функции существует тогда и только тогда, когда существуют и равны её односторонние производные.
Дифференциал функции. Пусть по-прежнему f определена в
Uδ (x0 ) .
Определение 1.6.1. Если существует такое число L , что для любого
x Uδ (x0 ) имеет место |
|
f (x) − f (x0 ) =L(x −x0 ) +o(x −x0 ) , |
(1.6.6) |
или, если обозначить x −x0 = x , |
|
f (x0 ) =L x +o( x) , |
|
то f называется дифференцируемой в точке x0 , а произведение L |
x на- |
зывается её дифференциалом в точке x0 , вычисленным при приращении аргумента, равном x .
Обозначается дифференциал символом |
df (x0 ) . Таким образом |
df (x0 ) =L x . Заметим, что если рассмотреть функцию y =x , то |
|
y(x0 + x) − y(x0 ) = x =1 |
x +0 . |
Очевидно, что ноль есть величина более высокого порядка малости, чем
x : 0 =o( |
x) , поэтому y =x дифференцируема в любой точке x0 R , при |
этом L =1, |
то есть dy =dx =1 x = x . Поэтому обычно выражение для |
дифференциала функции f записывают в следующей форме: df (x0 ) =L dx .
Пример. Пусть f (x) =x3 . Найдём df (x0 ) :
f (x0 ) =(x0 +dx)3 −x03 =x03 +3x02 dx +3x0 (dx)2 −x03 =3x02 dx +3x0 (dx)2 .
Очевидно, 3x0 (dx)2 =o(dx) , следовательно, f дифференцируема, L =3x02 и
df (x0 ) =3x02 dx .
Однако, такой способ (основывающийся только на определении), очевидно, не годится для достаточно сложных функций. Поэтому встаёт задача: во-первых, выяснить условия, при которых дифференциал f суще-
ствует, во-вторых, найти формулу для его вычисления.
90
