Zabotin_Dulliev_Chernyaev_-_Mat_an

f (n) (x) не определена ни в какой точке, кроме x0 , поэтому воспользуемся

первым правилом, находя отношение производных, вычисленных в точке x0 , тогда, очевидно, производная числителя в точке x0 имеет вид

f (n) (x0 ) − f (n) (x0 ) =0 ,

а производная знаменателя равна n! Таким образом, предел выражения (1.6.31), вычисленный в точке x0 , равен нулю, а следовательно, мы доказа-

ли, что Rn (x) =o((x −x0 )n ) .

Замечание. Форма Rn (x) =o((x −x0 )n ) называется формой Пеано.

Доказанная теорема оценивает скорость стремления остатка к нулю при условии стремления к нулю разности x −x0 . Во многих задачах анали-

за этого бывает достаточно. Однако, при использовании формулы Тейлора в приближённых вычислениях, т. е. при использовании формулы

f (x) ≈Tn (x) ,

эта теорема ничего не говорит о количественной оценке Rn (x) , т. е. о количественной оценке погрешности вычисления значения f в точке х.

Задачу такой оценки решает следующая теорема.

Теорема 1.6.15 (теорема об остатке формулы Тейлора в формах Коши и Лагранжа). Пусть f дифференцируема n +1 раз в некоторой ок-

рестности Uδ (x0 ) . Тогда найдутся θ1 ,θ2 (0; 1) такие, что для любого х из этой окрестности справедливы формулы:

любого t =x0 +θ(x −x0 ) , θ [0;1] функция ϕ(t) дифференцируема, посколь-

g(t) , также дифференцируемую при любом t Uδ (x0 ) , и применим к ϕ и g

111

формулу Коши на отрезке, соединяющем х и x0 : найдётся ξ=x0 +θ(x −x0 ) такая, что

квадратной скобки взаимно сокращается со вторым слагаемым следующей

Мы получили своего рода «полуфабрикат», из которого, выбирая тот или инойвид функции g , можнополучатьразличныеформыдляостатка Rn .

1. Положим g(t) =x −t . Тогда g / (t) =g / (ξ) =−1, g(x) =0 , g(x0 ) =x −x0 .

Подставляя эти выражения в (1.6.33), получим

Rn (x) = f (n+1) (ξ) (x −ξ)n (x −x0 ) . n!

Поскольку ξ = x0 + θ1 (x − x0 ) , то

112

(x −ξ) n = (x − x0 − θ1 (x − x0 )) n = (1 − θ1 ) n (x − x0 ) n

и последнее выражение примет вид

Rn (x) = f (n+1) (x0 +nθ!1 (x − x0 )) (1 − θ1 ) n (x − x0 ) n+1 ,

т. е. формула Коши получена.

2. Положим g(t) =(x −t)n+1 , тогда g / (ξ) =−(n +1)(x −ξ)n , g(x0 ) =(x −x0 )n+1 , g(x) =0 . Подставив эти выражения в (1.6.33), получаем (после очевидных сокращений)

т. е. форма Лагранжа получена. Теорема доказана.

Наиболее удобной формой является форма Лагранжа. Она удобна и для запоминания: остаток имеет тот же вид, что и (n+1)-й член многочлена Тейлора с той разницей, что (n+1)-я производная вычисляется не в точке x0 , а в некоторой промежуточной точке между х и x0 . Однако (впрочем, в редких случаях) приходится использовать форму Коши из-за невозможности произвести соответствующие оценки с помощью формы Лагранжа.

Разумеется, полученные формы не могут нам дать точного значения Rn (x) , поскольку местоположение ξ между х и x0 точно нам не известно.

Однако, это не так страшно – в вычислительных задачах нас интересует не точное значение погрешности вычислений, а оценка этой погрешности; например, нужно вычислить значение f (x) с точностью до десятого знака

после десятичной запятой. В этом случае мы добиваемся выполнения неравенства Rn (x) ≤10−11 . Как это делается, мы увидим из нижеследующих

примеров.

Заметим, наконец, что для формулы Маклорена

113

Примеры формулы Маклорена для некоторых элементарных функций.

Следовательно, в форме Лагранжа остаток примет вид:

Заметим, что при записи последней формулы можно «сэкономить»: поскольку на самом деле в представлении sin x содержится член с чётным

x2k +2

индексом 0 (2k +2)!, равный нулю, то у остаточного члена можно на еди-

ницу повысить порядок, как бы учитывая в формуле это нулевое слагаемое:

Пусть теперь перед нами стоит задача: вычислить sin1,2 с точностью

ε=10−4 . Для того чтобы добиться этой точности, необходимо найти n, для которого имеет место:

114

Очевидно, найденное n удовлетворяет и (1.6.34). А это неравенство решаем перебором n, что очень несложно, в особенности, с помощью калькулятора или ЭВМ. В данном случае неравенство (1.6.34) выполняется уже при n =3 и, следовательно,

sin(1,2) ≈1,2 −(1,32!)3 + (1,52!)5 −(1,72!)7

сточностью ε=10−4 . Выражение, стоящее справа, уже легко вычислить.

2.f (x) =cos x . С помощью рассуждений, аналогичных приведённым

выше, можно получить формулу:

cos x =1− x22! + x44! −...+(−1)n (x2n2n)!+R2n+1 (x) ,

где Rn снова может быть записан в различных формах.

3. f (x) =ex . Поскольку для любого n имеет место (ex )(n) =ex , то формула Маклорена записывается просто:

а формула Лагранжа для Rn (x) имеет вид:

Rn (x) =(ne+θx1)!xn+1 .

Из этого разложения, в частности, следует формула, по которой сколь угодно точно можно приблизиться к числу е: при x =1 имеем

Поскольку (n +11)! – быстро убывающее с ростом n выражение, то

требуемая точность достигается достаточно быстро.

В учебниках и задачниках по математическому анализу можно найти формулу Маклорена и для других функций. Например, для f (x) =ln(1+x) ,

f (x) =(1+x)α и др. Здесь мы ограничимся приведёнными примерами.

Применения формулы Тейлора к исследованию функций.

Мы уже отмечали выше, что теорема Ферма не даёт достаточных условий экстремума функции. Теперь мы готовы сформулировать и доказать соответствующую теорему.

Теорема 1.6.16 (о достаточных условиях строгого экстремума).

Пусть f имеет n производных в точке x0 , при этом

115

Тогда, если n - чётное число, то x0 – точка строгого экстремума, а имен-

но, если f (n) (x0 ) >0 , то x0 – точка строгого минимума, если f (n) (x0 )<0 – строгого максимума. Если n – нечётное число, то экстремума в точке x0 нет.

Доказательство. Условия теоремы позволяют записать для f фор-

мулу Тейлора с остатком в форме Пеано для любого х из окрестности точки x0 . Учитывая (1.6.35), получим:

f (x) = f (x0 ) + f (n) (x0 ) (x −x0 )n +o((x −x0 )n ) , n!

ности. Но тогда в этой окрестности знак квадратной скобки будет положительным. Также, в силу чётности n, положительным будет и знак сомножи-

т. е. x0 – точка строгого минимума.

Аналогичные рассуждения при f (n) (x0 )<0 приводят нас к тому, что x0 – точка строгого максимума.

мальная точка и при f // (x0 ) >0 ( f // (x0 )<0 ) это точка строгого минимума (максимума) функции f .

Кроме точек экстремума, интересными точками графика функции являются точки перегиба и связанные с ними точки выпуклости и вогнутости.

Определение 1.6.5. Пусть f определена хотя бы в некоторой окрестности точки x0 и существует f / (x0 ) . Точка x0 называется точкой вы-

116

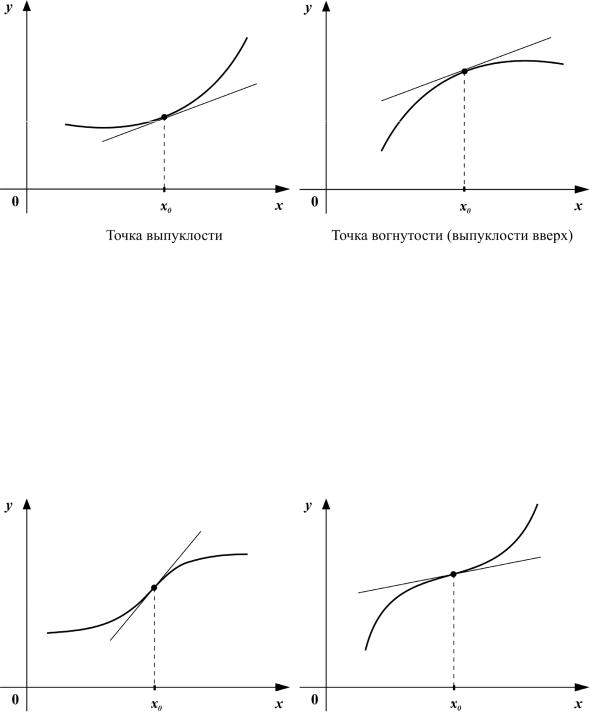
пуклости (вогнутости) графика функции f , если найдётся такая Uδ (x0 ) , что

В частности (как видно из определения), точка минимума функции f является точкой выпуклости её графика, а точка максимума – точкой

вогнутости. Иногда точки вогнутости графика f называют точками вы-

пуклости вверх графика.

Геометрический смысл введённых определений ясен:

Пусть f по-прежнему определена хотя бы в окрестности точки x0 и существует f / (x0 ) . Точка x0 называется точкой перегиба графика f , если существует такая окрестность Uδ (x0 ) , что

117

Таким образом, график функции для x Uδ (x0 ) расположен по разные стороны касательной, проведённой к графику f в точке (x0 , f (x0 ) ).

Если для x ≠x0 все неравенства (1.6.36) и (1.6.37) выполняются стро-

го, то говорят о строгой выпуклости, строгой вогнутости и о строгом перегибе в точке x0 .

Теорема 1.6.16 (о достаточном условии точки перегиба). Пусть f

имеет n производных в точке x0 . Пусть также имеют место условия: f // (x0 ) = f /// (x0 ) =...= f (n−1) (x0 ) =0 ; f (n) (x0 ) ≠0 .

Тогда:

1)если n – чётное число и f (n) (x0 ) >0 , то x0 – точка строгой выпуклости графика f ;

2)если n – чётное число и f (n) (x0 )<0 , то x0 – точка строгой вогнутости графика f ;

3)если n – нечётное число, то x0 – точка строгого перегиба графика функции f .

Опять, как и в теореме 1.6.15, выберем окрестность Uδ (x0 ) такую, что квадратная скобка сохранит в этой окрестности тот же знак, что и f (n) (x0 ) . Тогда в этой окрестности возможны следующие рассуждения:

1. если n чётно и f (n) (x0 ) >0 , то

~ /

x Uδ (x0 ) f (x) − f (x0 ) − f (x0 )(x −x0 ) >0 ,

т. е. тогда x0 – точка строгой выпуклости графика f ; 2. если n чётно и f (n) (x0 )<0 , то

~ /

x Uδ (x0 ) f (x) − f (x0 ) − f (x0 )(x −x0 )<0 ,

т. е. тогда x0 – точка строгой вогнутости графика f ;

3. если n нечётно, то (x −x0 )n имеет разные знаки слева и справа от

~

x0 (разумеется, при этом x Uδ (x0 ) ), а значит, и выражение

f (x) − f (x0 ) − f / (x0 )(x −x0 )

имеет разные знаки по разные стороны от x0 , т. е. x0 – точка строгого перегиба графика f . Теорема доказана.

118

В заключение этого раздела рассмотрим ещё одно понятие, не связанное напрямую с понятием производной, но необходимое при исследовании так называемого асимптотического поведения графика функций – «поведение графика при удалении его точки в ∞». Выражение, взятое в кавычки, конечно, никак не может быть взято в качестве определения асимптотического поведения f в силу его полной неопределённости и, в

общем-то, безграмотности. Поэтому перейдём к строгим определениям. Пусть f определена в проколотой окрестности точки а. Прямая

x =a называется вертикальной асимптотой графика f (или вертикаль-

ной асимптотой f ), если хотя бы один из односторонних пределов

является бесконечным.

Например, f (x) =1x имеет вертикальную асимптоту x =0 .

Пусть f определена на (a;+∞) . Прямая y =kx +b называется правой наклонной асимптотой f , если

lim (f (x) −(kx +b))=0 .

x→+∞

При k =0 наклонную асимптоту часто называют горизонтальной асимптотой.

Например, f (x) =1x sin x , x (0;+∞) . Легко видеть, что y =0 – правая

горизонтальная асимптота.

Очевидным образом вводится понятие левой наклонной асимптоты: если f определена на (−∞; a) , то y =kx +b назовём левой наклонной (соот-

ветственно горизонтальной) асимптотой функции f , если

lim (f (x) −(kx +b) )=0 .

x→−∞

Теорема 1.6.17. Для того чтобы прямая y =kx +b была правой (левой) наклонной асимптотой функции f , необходимо и достаточно, чтобы

Доказательство проведём для правой асимптоты. Необходимость. Пусть y =kx +b – правая асимптота, тогда

119

т. е. y =kx +b – асимптота. Теорема доказана.

Исследование графика функции в целом.

Доказанные результаты позволяют составить примерную последовательность шагов, которые нужно сделать при исследовании графика функции.

1)Найти область определения функции D( f ) .

2)Если D( f ) симметрична относительно нуля, определить её чётность, нечётность или прийти к выводу, что f – функция общего вида.

3)Найти асимптоты функции.

4)Найти экстремальные точки f .

5)Определить участки монотонности f .

6)Найти точки перегиба и промежутки сохранения выпуклости (вогнутости).

Найденные данные, после их систематизации, позволяют определить принципиальный характер графика функции.

Вопросы для самопроверки.

1. Пусть f / (x0 ) существует. Обязана ли существовать f / (x) хотя бы в некоторой окрестности точки x0 ? Иными словами, существуют ли функ-

ции, дифференцируемые в единственной точке? Для ответа на вопрос рассмотрите функцию

Что это означает?

3. Пусть f определена в окрестности точки x0 и для любой последовательности xn со значениями из этой окрестности выполняется условие:

120