Zabotin_Dulliev_Chernyaev_-_Mat_an

Мы не будем напоминать десятичные представления чисел и правила работы с ними, напомним только, что числа, не представимые в форме

mn , n, m Z , называются иррациональными.

Вот теперь мы подошли к еще одной аксиоме, которая в школьном курсе математики играет не столь важную роль, как аксиомы, введенные выше, и, поэтому, недостаточно изучаемая или не изучаемая вовсе. Однако для

нас эта аксиома,– аксиома непрерывности R,– будет играть основополагающую роль, поскольку в дальнейшем анализ функций будет строиться на фундаментальном понятии предельного перехода.

Ответ на вопрос: «Есть ли на R дырки, не заполненные числами?» – может показаться очевидным в силу наших интуитивных представлений о прямой как о геометрическом объекте.

Но, оказывается, этот вопрос можно решить только на уровне его постулирования (аксиоматизации).

При этом, как часто случается в математике, можно предложить несколько эквивалентных формулировок аксиомы. В этом случае, приняв одну из формулировок за аксиому, остальные мы делаем теоремами о необходимых и достаточных условиях.

Приведем две из таких эквивалентных аксиом (их эквивалентность, однако, доказывать не станем).

1. Аксиома о дедекиндовом сечении.

Здесь и далее для двух числовых множеств A и B будем писать A ≤ B в том и только в том случае если: a A b B : a ≤ b .

Определение 1.3.4. Пара числовых множеств A,B таких, что а) A, B ≠ ;

б) A B = R ;

в) A ≤ B ,

называется дедекиндовым сечением поля R.

Иногда к требованиям а)– в) добавляют:A ∩ B = , хотя это требование необязательно.

Для каждого сечения A, B существует элемент секущим элементом, такой, что A ≤ ρ ≤ B .

Отсюда легко следует: а) секущее число единственно, б) если

A ∩ B ≠ , то A ∩ B ={ρ} .

Впервые понятие сечения и секущего числа предложено немецким математиком Р. Дедекиндом, что и объясняет название аксиомы.

2.Аксиома о существование точных граней.

Если для непустого множества A R существует число b такое, что A ≤ b ( A ≥ b) , то среди всех таких чисел существует наименьшее (наибольшее).

31

Мы рекомендуем самостоятельно порассуждать об эквивалентности этих аксиом.

В дальнейшем изложении мы примем аксиому о существование точных граней и вернемся к ней более подробно ниже. Это объясняется лишь тем,

что такой способ аксиоматизации непрерывности R позволяет обойти некоторые технические сложности, опуская несущественные для нас подробности.

Определение 1.3.5. Поле R называется числовой прямой, если в нем принята какая-либо из аксиом непрерывности.

Элементы поля R именно с этого момента будем называть действи-

тельными числами.

Вопросы и задания для самопроверки.

1. Пусть на множестве неотрицательных действительных чисел R+ задана бинарная операция ϕ : a,b R : aϕb = max{a;b} . Будет ли эта операция групповой?

2. На множестве пар (x, y); x, y R определим операцию «+»: (x1 , y1 )+(x2 , y2 )= (x1 + x2 , y1 + y2 ). Будет ли эта операция групповой?

3.Можно ли операцию скалярного произведения, введенную на множестве плоских векторов, называть бинарной? А операцию векторного произведения?

4.Пусть на множестве всех пар (x, y); x, y R задана операция умно-

жения: (x1 , y1 ) ×(x2 , y2 ) = (x1 x2 − y1 y2 , x1 y2 + x2 y1 ) . Убедитесь, что это групповая операция.

5.Доказать, что если на множестве пар, о которых говорится в упражнении 4, ввести операцию сложения так, как это сделано в упражнении 2, то введенные операции будут удовлетворять аксиоме дистрибутивности.

6.Доказать:

a)a R : a 0 = 0;

б) a R : −a = (−1) a; в) a R : −(−a) = a;

г) 1>0 (указание: доказать 1 ≠ 0 , потом положить противное и умножить обе части на положительное число).

7. На декартовой плоскости XOY , рассматриваемой как множество упорядоченных пар (x, y); x, y R , заданы множества:

a) T1 ={(x; y) 0 ≤ x ≤1,0 ≤ y ≤1}; б) T2 ={(x; y) x ≥ y};

в) T3 ={(x; y) x = y};

32

Какое из них является отношением частичного порядка (линейного порядка) на числовой прямой R?

г) T4 ={(x; y) y = sin x};

д) T5 ={(x; y) y1 ≠ y2 x1 ≠ x2 };

Можно ли эти множества называть графиком какой-либо функции?

8. Аналогично соответствующим теоремам для операции «+», доказать теоремы для операции «×»:

а) единица единственна;

б) для a ≠ 0, элемент a −1 единственен; 9. Доказать правила работы с дробями:

a) m p = m p ; n k n k

m

б) np = mn pk ;

33

1.3.2. Числовые множества и последовательности

Любое подмножество числовой прямой R будем называть числовым множеством.

Например: N – натуральный ряд чисел; Z – множество всех целых чисел; [a, b]={x R: a <x <b} – отрезок; (a, b) ={x R: a <x <b} – интервал

и т.д.

Множество

Uε (x0 ) ={x R: x0 −ε<x <x0 +ε, ε>0}={x R: x −x0 <ε}

~

называется ε-окрестностью точки x0 ; множество Uε (x0 ) =Uε (x0 )\ {x0 } –

проколотой ε-окрестностью точки x0 ; множества

Uε+ (x0 ) ={x R: x0 <x <x0 +ε, ε>0} и Uε− (x0 ) ={x R: x0 −ε<x <x0 , ε>0}

называются соответственно правой и левой полуокрестностью точки x0 , число ε>0 называется радиусом окрестности или полуокрестности.

Напомним, что множество называется счётным, если между ним и натуральным рядом чисел N можно построить биекцию.

Отметим несколько общих свойств счётных множеств.

Свойство 10. Множество, равномощное счётному множеству, в свою очередь счётно.

Доказательство. Пусть А – счётное множество, а В – равномощно множеству А. Тогда существуют две биекции: f : N →A, g: A→B . Но то-

гда F =g o f также биекция и F: N →B , что и требовалось.

Свойство 20. Бесконечное подмножество K N является счётным множеством.

Доказательство. Расположим элементы K в порядке их возрастания: K ={a, b, c,...}. Тогда элемент а можно поставить во взаимноодно-

значное соответствие с единицей: 1↔a , элемент b: 2 ↔b и т. д. Таким об-

разом, каждое натуральное число из K будет иметь некоторый номер из N, при этом наоборот, каждый номер из N будет присвоен некоторому элементу из K , поскольку K бесконечно, что и требовалось.

Свойство 30. Любое бесконечное подмножество счётного множества вновь счётно.

Доказательство. Если А – счётное множество и A B бесконечно, то В равномощно некоторому бесконечному подмножеству K N и так как К счётно (свойство 20), то В также счётно (свойство 10).

Определение 1.3.6. Если K – бесконечное подмножество N (может быть K = N ), то любая функция f : K →B называется последовательно-

стью со значениями в В.

При изучении свойств последовательностей будем полагать для простоты, что K = N .

Если B R , то последовательность называется числовой.

34

Таким образом, последовательность – это функция натурального аргумента. Её значения f (n) принято обозначать xn .

волом xn будем обозначать и саму последовательность, т. е. функцию, точно так же, как функцию f аргумента x часто обозначают f (x) , имея в виду не значение f в точке x , а именно функцию f .

В дальнейшем мы часто будем рассматривать последовательности множеств An , понимая под этим функцию N →{A}, где {A} – множество

подмножеств некоторого заданного множества Х, например:

An ={1, 2,..., n}, n =1, 2,...,

т. е. здесь каждому n N ставится в соответствие множество, состоящее из n первых элементов натурального ряда, или

Здесь каждому n N ставится в соответствие отрезок:

A1 =[1; 1+1], A2 = 1;1+ 12 , A3 = 1; 1+13 и т. д.

Конечно, рассмотренные в этих примерах последовательности нельзя называть числовыми, поскольку их значениями являются не числа, а числовые множества.

Напомним, что рациональным числом называется несократимая дробь mn ; m, n Z , n ≠0 . То есть числа 1449 , − 279 , 1575 отождествляются с чис-

лами 72 , −13, 5 и т.д.

Теорема 1.3.3. Множество всех рациональных чисел счётно.

Доказательство. Построим таблицу следующим образом. В первую строку поместим все целые числа в порядке возрастания их абсолютных величин, ставя после натурального числа противоположное ему по знаку:

0; 1; −1, 2, −2; ... ; n; −n; ... n N .

Во вторую строку поставим все несократимые дроби со знаменателем 2, вновь упорядочив их по абсолютной величине и сохраняя то же, что и в первой строке, чередование знаков:

12; −12; 32; − 32; 52; −52; ...

Вообще, в n-ю строку поставим все несократимые дроби со знаменателем n, упорядочивая их по абсолютной величине и ставя после каждого положительного числа противоположное ему по знаку.

Тогда получим таблицу (матрицу) с бесконечным числом строк и столбцов. Ясно, что в этой таблице содержатся все рациональные числа.

Теперь легко установить биекцию между N и элементами этой таб-

лицы:

35

xn хотя бы одной цифрой: pnn ≠qn . Полученное противоречие и доказывает

теорему.

Следствие 1. Любой интервал (a; b) R несчётен.

Доказательство. Легко проверить, что отображение y =a +x(b −a), x (0;1)

является биекцией между (0;1) и (a; b) :

x = by−−aa , y (a; b) .

Следствие 2. Числовая прямая R – несчётное множество.

Доказательство. Одна из возможных биекций tg : −π2; π2 ↔(−∞; +∞).

При этом −π; π по предыдущему следствию – множество несчётное.

2 2

Замечание. Попутно мы увидели, что числовая прямая R равномощна любому интервалу (a; b) R .

Теорема 1.3.5. На любом интервале имеются как рациональные, так и иррациональные числа.

Доказательство. Если бы на интервале (a; b) не было иррациональ-

ных чисел, то он был бы счётным, что невозможно.

Пусть x (a; b) – иррациональное число, то есть a <x <b .

Пусть x =P, p1 p2 ... pn ... – десятичное представление числа х. Число yn =P, p1 p2 ... pn , полученное из х отбрасыванием всех цифр, стоящих после pn , – рациональное число. Тогда x − yn =0, 0...0 pn+1 pn+2 ...<10−n . Очевидно,

можно номер n подобрать настолько большим, что будет выполнено неравенство:

x − yn <10−n <min{ x −a ; x −b }, то есть a < yn <b .

Следствие 1. На любом интервале бесконечечно много как рациональных, так и иррациональных чисел.

Доказательство. Если бы иррациональных чисел было конечное число, то, отбрасывая их, мы получили бы счётное множество, что, очевидно, невозможно.

То, что кроме построенного выше yn на (a; b) найдётся ещё рациональное число – это очевидно: например, по доказанному, на (a; yn ) долж-

но вновь найтись рациональное число. Но тогда среднее арифметическое этого числа и yn – вновь рациональное число, лежащее на (a; b) . Даль-

нейшее рассуждение очевидно.

Следствие 2. Множество рациональных чисел, лежащих в любом интервале (a; b) , счётно.

37

Доказательство очевидно: множество рациональных чисел интервала (a; b) , являясь бесконечным подмножеством счётного множества, вновь

счётно.

Определение 1.3.8. Множество A R называется ограниченным сверху (снизу), если существует такое число b (число а), что для всех x A выполняется неравенство x ≤b (x ≥a) .

Число b (число а) называют верхней (нижней) границей множества А. Если А ограничено и сверху, и снизу, его называют ограниченным.

Из определения ясно, что если множество ограничено сверху (снизу), то у него бесконечно много верхних (нижних) границ.

Определение 1.3.9. Если существует наименьшая из всех верхних границ множества А, то она называется верхней гранью множества А и обозначается sup A (от латинского слова supremum – наибольший). Если

существует наибольшая из всех нижних границ множества А, то она называется нижней гранью множества А и обозначается inf A (от латинского

слова infimum – наименьший).

Запишем эти определения в «символической форме»:

Число S называется верхней гранью А, если:

1)x A: x ≤S ;

2)(ε>0) ( xε A): xε >S −ε.

Первое требование означает, что S – верхняя граница А, второе требование показывает, что любое число, меньшее чем S перестаёт быть верхней границей А.

Аналогично:

Число I называется нижней гранью А, если:

1)x A: x ≥I ;

2)(ε>0) ( xε A): xε <I +ε.

Вопрос о том, существуют ли у ограниченных множеств грани, supremum и infimum, относится к области, называемой основаниями математики, и, по существу, связан с аксиомой о непрерывности числовой прямой. В зависимости от того, в какой форме аксиоматизировать непрерывность R, существование граней числовых множеств может оказаться теоремой или аксиомой.

В данном курсе лекций мы пойдём по второму пути.

Аксиома о существовании граней у числовых множеств. Всякое ограниченное сверху числовое множество имеет верхнюю грань. Всякое ограниченное снизу числовое множество имеет нижнюю грань.

Непосредственным следствием из этой аксиомы является так назы-

ваемое свойство архимедовости числовой прямой, утверждающее неогра-

ниченность сверху натурального ряда чисел.

Теорема 1.3.6 (Архимед).

a R n N : n >a .

Доказательство. Предположим противное:

38

a R n N : n≤a .

Тогда из аксиомы следует существование числа S R такого, что

1) n N : n≤S ; 2) ε>0 nε N : nε >S −ε.

Если теперь возьмём ε=1, то из 2) получим:

n1 N : n1 >S −1

или

n1 N : n1 +1>S .

Но последнее невозможно, поскольку n1 +1 N . Теорема доказана.

Следствие 1.

a R na N n >na : n >a .

Доказательство очевидно: по теореме Архимеда существует na N : na >a , но тогда из n >nε тем более следует n >a .

Теперь перейдём к аксиоматическому изучению числовых последовательностей. Сначала введём несколько определений.

1.Последовательность xn называется ограниченной сверху (снизу), если сверху (снизу) ограничено множество её значений {xn }.

2.Последовательность xn называется возрастающей (неубываю-

щей), если

n N : xn+1 ≥xn .

В случае, когда все неравенства являются строгими, последователь-

ность называется строго возрастающей (возрастающей). Для возрастаю-

щих xn примем обозначение xn ↑.

Очевидным образом вводится понятие убывающей последовательно-

сти

n N : xn+1 ≤xn

и строго убывающей последовательности. Для убывающей xn примем обо-

значение xn ↓.

Все убывающие и возрастающие последовательности объединяются общим названием монотонные последовательности.

3. Сужение последовательности xn на бесконечное подмножество K N называется подпоследовательностью последовательности xn и обо-

значается xn k .

Теперь введём важнейшее понятие сходящейся последовательности и её предела.

39

Говорят также: последовательность xn сходится к числу а и обозна-

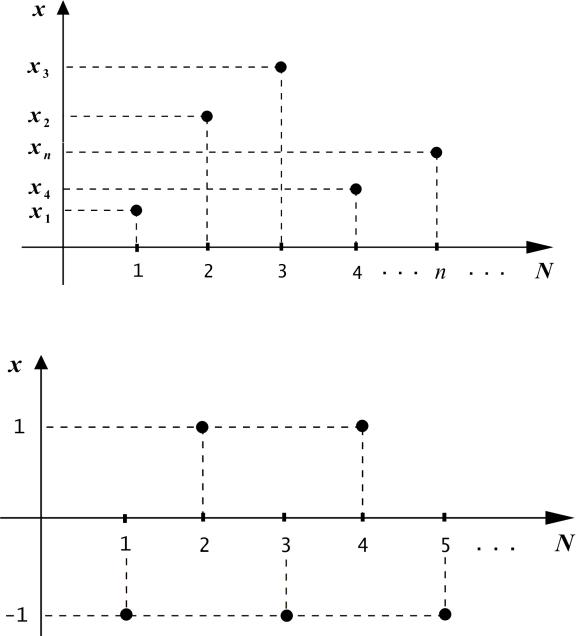
Как и у всякой числовой функции, у последовательности есть гра-

фик, т. е. множество точек на координатной плоскости с координатами

(n, xn ) . Ясно, что график – «неограниченное справа» множество:

Например, начало графика последовательности xn =(−1)n :

40