Zabotin_Dulliev_Chernyaev_-_Mat_an

Производные и дифференциалы порядка выше первого.

Пусть f имеет производную f / (x) в любой точке некоторой окрестности Uδ (x0 ) . Тогда f / (x) , в свою очередь, является функцией, опреде-

при этом существует ψ/ (x0 ) , то её называют третьей производной функции f в точке x0 и обозначают

f /// (x0 ) , или f (3) (x0 ) , или d 3 f (3x0 ) .

dx

Подобными рассуждениями можно ввести понятие производной любого порядка, если только производная предыдущего порядка позволяет это сделать.

Обозначают производные n-го порядка так:

f (n) (x0 ) , или d n f (nx0 ) , dx

а f называют n раз дифференцируемой в точке x0 .

Если функция имеет производные любого порядка, то её называют

бесконечно дифференцируемой в точке x0 . Так, например, f (x) =ex являет-

ся бесконечно дифференцируемой в любой точке x R .

По определению будем полагать, что производная нулевого порядка совпадает с f : f (0) (x0 ) = f (x0 ) .

Из определения следует, что когда говорится «пусть f дифференцируема n раз в точке x0 », то производная f (n−1) (x) определена в некоторой

101

Из вышеприведённой таблицы производных может возникнуть впечатление, что всякая функция непрерывно-дифференцируема в любой точке области определения. Однако, это не так. Рассмотрим пример:

Очевидно, при x ≠0 эта функция имеет производную: f / (x) =2xcos 1x +sin 1x .

Покажем, что f / (0) также существует:

ской индукции.

Упражнение. Докажите методом полной математической индукции формулу

ln(n) x =(−1)n+1 (nx−n1)! для всех x >0 .

Введём понятие дифференциалов высших порядков. Для этого будем предполагать, что f дифференцируема n раз в точке x0 ( n≥2 ).

102

скобки: d 2 f (x0 ) = f // (x0 )dx2 .

Ясно, что это степенная функция аргумента dx . Из определения также ясно, что если находить дифференциалы df и dϕ при заданном dx , то

второй дифференциал можно определить и так:

т. е. как «дифференциал дифференциала».

Аналогичным образом вводятся третий и т. д. дифференциалы:

Заметим, что дифференциалы порядка выше первого перестают обладать свойством инвариантности формы (точнее, оно сохраняется лишь в частных случаях).

Действительно, рассмотрим, например, d 2 f , считая, что все функ-

ции нужное число раз дифференцируемы. Пусть х – независимый аргумент, тогда

Если же x ≡x(t) , то

Мы видим, что в этом случае d 2 f (x(t)) отличается от d 2 f , вычисленного в (1.6.19), вторым слагаемым, стоящим в правой части. Формулы

Значит, (1.6.19) и (1.6.20) будут иметь одну и ту же форму лишь в том слу-

103

Часто бывает полезной формула, по которой можно найти производную любого порядка от произведения функций:

называемая формулой Лейбница. Здесь Cnk – биномиальные коэффициенты

и формула очень напоминает формулу бинома Ньютона. Вывод этой формулы также аналогичен выводу формулы бинома Ньютона. Действительно, положим, что (1.6.21) выполняется для n и докажем её для n+1:

т. е. получена формула (1.6.21), записанная для n+1. Поскольку при n =1 формула Лейбница имеет место (мы это доказали в теореме 1.6.2), то справедливость формулы (1.6.21) доказана методом полной индукции.

Применение производной для вычисления пределов функций. Правила Лопиталя.

Теорема 1.6.12 (первое правило Лопиталя). Пусть f и g диффе-

ренцируемы в точке x0 , f (x0 ) =g(x0 ) =0 и g / (x0 ) ≠0 , тогда имеет место формула

104

воспользоваться связью между пределами и односторонними пределами функций. Теорема доказана.

Доказанные правила позволяют найти пределы частного двух функций в конечной точке x0 при условии, что пределы обеих функций равны нулю. В этом случае говорят, что эти правила раскрывают неопределён-

ляющие раскрывать эту неопределённость в бесконечно удалённых точках,

частного двух функций при условии, что пределы каждой из функций бесконечны.

Рассмотрим два таких следствия.

105

Это следствие примем без доказательства.

Можно, наконец, показать, что следствие 2 остаётся справедливым и в случае, если x0 – бесконечно удалённая точка.

Ниже, при исследовании сходимости числовых рядов, нам понадо-

бится предел lim x x =1. Докажем его с помощью второго следствия. Обо-

x→+∞

значим y =x x . Если показать, что ln y →0 , то, в силу непрерывности

x→+∞

функции ln x , тем самым будет показано, что y →1. Очевидно,

x→+∞

106

lim ln y =0 , что и требовалось.

x→+∞

Формула Тейлора.

Эта формула играет первостепенную роль при исследовании функций как в теоретических задачах, так и при исследовании прикладных проблем, поэтому многие математики считают формулу Тейлора одним из наиболее существенных достижений математического анализа.

Напомним, что дифференцируемую в точке x0 функцию можно в окрестности этой точки представить в виде

f (x) = f (x0 ) + f / (x0 )(x −x0 ) +o(x −x0 ) .

Если в этой формуле пренебречь слагаемым o(x −x0 ) , то получится приближённая формула

ко, она имеет существенные недостатки. Во-первых, отбрасывая o(x −x0 ) ,

мы не знаем величину ошибки, которую мы допустим при этом, а значит, не знаем, с какой точностью вычислили значение f в точке х. Во-вторых,

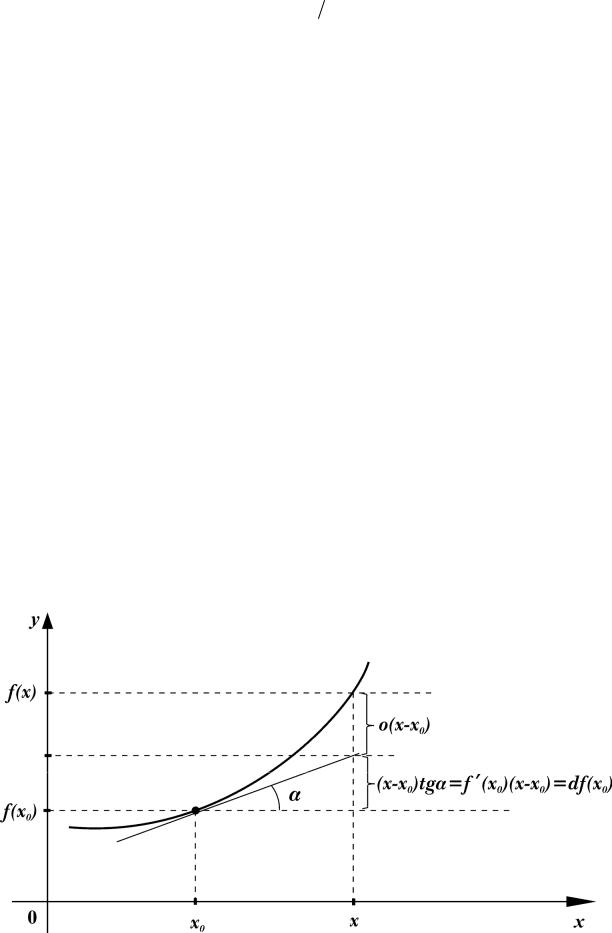
величина o(x −x0 ) достаточно быстро стремится к нулю при x→x0 , однако если х отстоит от x0 далеко, то значение o(x −x0 ) может быть столь большим, что ни о каком приближённом значении f (x) речи быть не может. Это можно проиллюстрировать следующим рисунком:

107

Из рисунка видно, что при удалении х от x0 величина o(x −x0 ) катастрофически возрастает, т. е. ошибка вычисления f (x) становится недопустимой. Но если бы удалось из o(x −x0 ) выделить её «главную часть», т. е. представить

o(x −x0 ) =a2 (x −x0 )2 +o2 ((x −x0 )2 ),

где a2 ≡const – некоторый известный нам коэффициент, то можно было бы записать

f(x) = f (x0 ) + f / (x0 )(x −x0 ) +a1 (x −x0 )2 +o1 ((x −x0 )2 )

иможно надеяться, что формула

f (x) ≈ f (x0 ) + f / (x0 )(x −x0 ) +a2 (x −x0 )2

будет точнее, чем формула (1.6.24) при том же самом значении х. Возникает вопрос: нельзя ли продолжить выделение главных частей возникающих остатков, с тем чтобы получить формулу

f(x) = f (x0 ) + f / (x0 )(x −x0 ) +a2 (x −x0 )2 +...+an (x −x0 )n +o((x −x0 )n ) ?

Если да, то до какого значения n это возможно и как найти коэффи-

циенты ai ?

Решение этого вопроса позволяет нам исследовать функцию f с помощью многочлена

Tn (x) = f (x0 ) + f / (x0 )(x −x0 ) +a2 (x −x0 )2 +...+an (x −x0 )n .

Это очень важно, поскольку многочлены составляют класс функций, свойства которых наиболее хорошо изучены; в частности, вычисление значений многочленов в любой точке х не составит труда при известных значениях коэффициентов и при известной точке x0 .

Итак, поставим следующую общую задачу: для f (x) найти много-

член

Tn (x) =a0 +a1 (x −x0 ) +a2 (x −x0 )2 +...+an (x −x0 )n

такой, чтобы в некоторой окрестности точки x0 выполнялось равенство f (x) =Tn (x) +o((x −x0 )n ) ,

Поскольку задача нахождения многочлена эквивалентна задаче нахождения его коэффициентов, то перед нами встаёт следующая проблема: найти формулы для вычисления ak , k =0,1,..., n .

Задачи подобного рода в математике часто решаются следующим образом: возьмём для начала наиболее «хороший» класс функций f и для

него решим поставленную задачу, а затем возьмём f из более широкого

класса и попытаемся на этот класс перенести полученные результаты. Так мы и поступим. Поскольку наиболее хорошими (наиболее хорошо изучен-

108

ными) функциями являются многочлены, то возьмём f в виде некоторого многочлена с известными коэффициентами:

f(x) =Pn (x) = p0 + p1 x + p2 x2 +...+ pn xn

инайдём коэффициенты ak , k =0,1,..., n так, чтобы выполнялось

Из формулы (1.6.25) следует, что Pn (x0 ) =a0 . Продифференцируем k раз (1≤k ≤n ) обе части равенства (1.6.25), при этом заметим, что k-я производная слагаемых ai (x −x0 )i при i <k будет тождественно равна нулю, при

Формула (1.6.26) показывает, что формула (1.6.26) имеет вид:

Пусть теперь f – некоторая функция, n раз дифференцируемая в точке x0 . Попытаемся строить Tn (x) по тем же формулам, т. е. построим Tn (x) с коэффициентами

Коэффициенты (1.6.27) будем называть коэффициентами Тейлора функции f , многочлен (1.6.28) – многочленом Тейлора функции f , фор-

мулу (1.6.30) – формулой Тейлора для функции f , а функцию Rn (x) , по-

строенную по формуле (1.6.29) – остатком (остаточным членом) форму-

лы Тейлора.

109

При x0 =0 коэффициенты, многочлен и формула носят имя Маклорена: формула Маклорена и т. д.

Насколько успешно решена задача представления f (x) с помощью многочлена Tn (x) , теперь зависит от поведения Rn (x) и от того, насколько успешно мы можем оценить его величину, поскольку Rn (x) и есть та самая

погрешность, которую мы допустим при использовании приближённого равенства

f (x) ≈Tn (x) .

На эти вопросы нам ответят следующие две теоремы.

Теорема 1.6.14 (об остатке формулы Тейлора в форме Пеано).

Пусть f дифференцируема n раз в точке x0 , тогда существует окрестность Uδ (x0 ) такая, что

x Uδ (x0 ) : Rn (x) =o((x −x0 )n ) .

Доказательство. То, что f дифференцируема n раз в точке x0 по определению означает существование окрестности Uδ (x0 ) , в которой определены как сама функция f , так и все её производные до порядка n −1 включительно. Пусть x Uδ (x0 ) . Чтобы доказать теорему, покажем, что

или, что то же самое (см. формулу 1.6.29):

крытию этой неопределённости вновь применить второе правило Лопиталя. Ясно, что вновь находя отношения производных, мы опять получим

Продолжая эти рассуждения n −1 раз, мы придём к необходимости

R(n−1) (x)

раскрыть неопределённость в выражении n!(n x −x0 ) , т. е. в выражении

110