Zabotin_Dulliev_Chernyaev_-_Mat_an

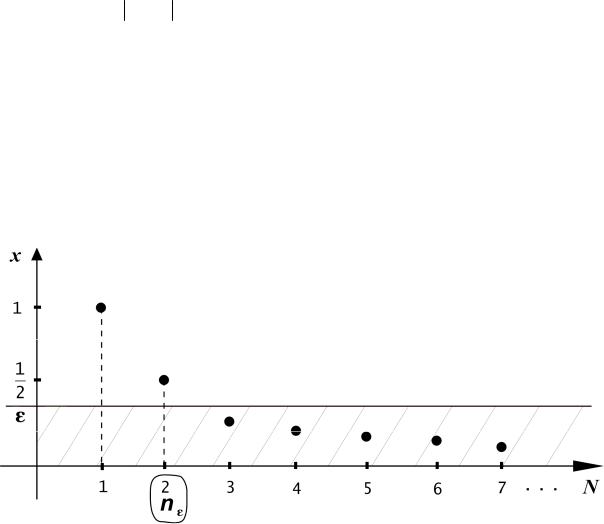
Uε (0) nε N n >nε : xn Uε (0) .

Легко видеть из определений, что xn →a тогда и только тогда, когда αn =xn −a является бесконечно малой последовательностью. Этим фактом мы будем широко пользоваться.

Наконец, сходимость xn к а можно интерпретировать и так: если рассматривать xn −a как расстояние между значениями последовательности (членами последовательности) и точкой а, то сходимость xn к а есть ни что иное, как стремление к нулю расстояния между xn и а.

Графически понятие сходимости xn к а означает, что какой бы ширины полосу, содержащую прямую x =a мы ни взяли, начиная с некоторого номера (шага) график xn будет лежать в этой полосе для всех последующих значений n.

Например, для последовательности xn =1n можно пояснить сказанное на рисунке:

Из рисунка можно догадаться, что lim 1n =0 , но, конечно, это нам

предстоит доказать строго.

Следствие 2 из теоремы Архимеда:

lim 1 =0 .

n n

Доказательство. Возьмём любое ε>0 , тогда по теореме Архимеда (точнее, по следствию 1 к ней):

nε N n >nε : n >1ε

или, что то же самое

ε>0 nε N n >nε : 1n <ε,

что и требовалось.

41

Свойства сходящихся последовательностей.

10. Сходящаяся последовательность ограничена. (Необходимое ус-

ловие сходимости.)

Доказательство. Пусть xn →a , то есть

ε>0 nε N n >nε : a −ε<xn <a +ε,

отсюда следует, что, начиная с номера nε +1, множество значений после-

довательности ограничено. Если положить

d =max {ε, a −x1 , a −x2 ,..., a −xn },

то для всех n N получим a −d ≤xn ≤a +d , что и требовалось.

20. Сходящаяся последовательность имеет единственный предел.

Доказательство. Пусть xn →a, xn →b, a ≠b . Тогда

a −b = (a −xn ) +(xn −b) ≤ a −xn + xn −b .

Поскольку ε>0 n1 N n >n1 : xn −a <ε/2 и в то же время

n2 n >n2 : xn −b <ε/2 ,

то n >n0 =max {n1 , n2 } оба неравенства выполняются сразу, т. е. a −b <ε для любого ε>0 , но этого быть не может, поскольку a −b – фиксирован-

ное положительное число.

30. Любая подпоследовательность сходящейся последовательности сходится к тому же пределу.

Доказательство очевидно: если xn −a <ε при всех n >nε , то и при

всех nk >nε имеет место xnk −a <ε.

40. Если последовательность возрастает и ограничена сверху, то она сходится. (Достаточное условие сходимости.)

Доказательство. Обозначим S =sup xn – верхнюю грань множества

значений xn . Очевидно, она существует. Тогда

1) n N : xn ≤S ; 2) ε>0 nε N : xnε >S −ε.

Но n >nε : xn >xnε , то есть

ε>0 nε n >nε : S −ε<xn ≤S <S +ε.

Таким образом xn →S .

50. Если последовательность убывает и ограничена снизу, то она сходится.

Доказать самостоятельно.

60. Пусть xn – ограниченная, αn – бесконечно малая последовательность, тогда последовательность yn =xn αn также бесконечно малая.

Доказательство. Пусть m =const такова, что n N : xn ≤m. Тогда

pn =xn + yn ; qn =xn − yn ; rn =xn yn ; tn = xn yn

42

сходятся к числам a +b, a −b, a b и ba (если b ≠0 ) соответственно.

Доказательство. Все утверждения доказываются аналогично. Докажем, например, что xn yn →ab , для этого запишем очевидные неравенства:

xn yn −ab = xn yn −xnb +xnb −ab ≤

для всех n >nε .

Замечание. При доказательстве мы «молчаливо» воспользовались предположением b ≠0 , когда записали дробь 2εb . Как изменится доказа-

тельство, если b =0 ?

Теоремы о предельных переходах в неравенствах.

Здесь и далее нам понадобится лемма, которую мы назовём

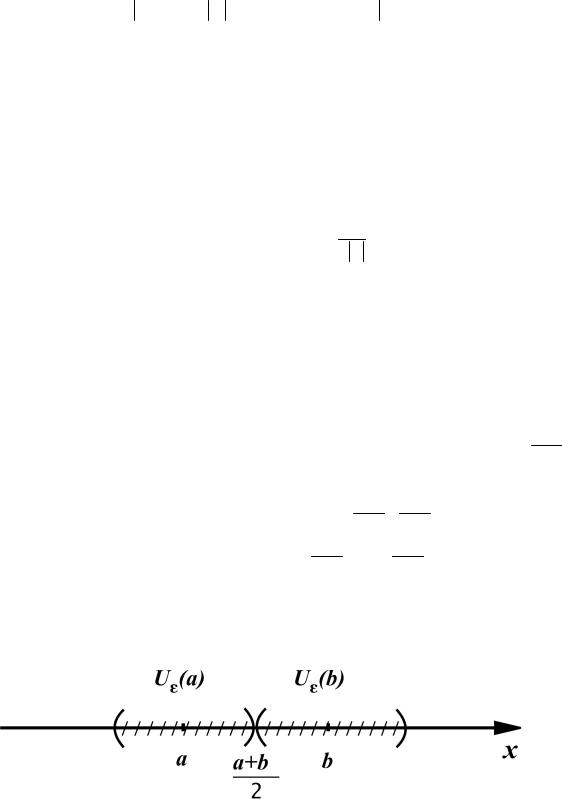
Лемма об отделимости. Пусть a, b R, a ≠b , тогда найдутся Uε (a)

и Uε (b) такие, что Uε (a)IUε (b) = .

Доказательство. Пусть, для определённости, a <b . Возьмём ε=b −2 a

и построим с этим радиусом Uε (a) и Uε (b) . Тогда

x Uε (a) a −ε<x <a +ε x<a +b −2 a = a +2 b ; y Uε (b) b −ε<x <b +ε b −b −2 a < y a +2 b < y .

Таким образом, мы видим, что для всех x Uε (a) и всех y Uε (b) выполняется неравенство x < y , но это значит, что Uε (a) и Uε (b) не имеют общих точек. Геометрический смысл доказанной леммы очевиден:

Замечание. В подобных случаях будем писать: Uε (a)<Uε (b) .

43

Теорема 1.3.7. Если xn →a и yn →b и при этом, хотя бы начиная с некоторого номера, xn ≤ yn , то a ≤b .

Доказательство. Предположим противное: a >b , тогда по лемме об отделимости найдутся Uε (a) и Uε (b) такие, что Uε (b)<Uε (a) , но тогда,

последовательностями, например, xn =a, n N . Как сформулируется тео-

рема в этом случае?

Теорема 1.3.8. Если xn →a, yn →b и a <b , то, начиная с некоторого

номера, xn < yn .

Доказательство. Вновь отделим a и b окрестностями и тогда, начиная с некоторого номера, выполнится xn < yn .

Замечание. Здесь, в отличие от предыдущей теоремы, существенно, что неравенство a <b строгое. Почему?

Теорема 1.3.9 (о сжимающих последовательностях). Пусть xn →a, yn →a и, хотя бы начиная с некоторого номера, xn ≤zn ≤ yn , тогда

zn →a .

Доказательство. Пусть ε>0 . Найдутся номера n1 , n2 , n3 такие, что:

n >n1 : a −ε<xn <a +ε;

n >n2 : a −ε< yn <a +ε;

n >n3 : xn ≤zn ≤ yn .

Тогда n >max {n1 , n2 , n3 }: a −ε<xn ≤zn ≤ yn <a +ε, что и требовалось.

Так же как аксиома о гранях числовых множеств и теорема Архимеда, к основаниям математики относится решение следующего вопроса. Пусть дана последовательность числовых множеств An таких, что каждое из них непусто и для всех n N : An+1 An (такие последовательности мно-

жеств называют вложенными или убывающими). Спрашивается: можно ли гарантировать непустоту их пересечения (наличие у них хотя бы одной общей точки); в каких случаях можно гарантировать непустоту пересечения этих множеств?

На первый вопрос ответ будет отрицательным. Действительно, рассмотрим An = 0; 1n , n =1, 2,... – последовательность интервалов, очевидно,

убывающую. Легко понять, что у них нет ни одной общей точки, поскольку точка 0 не принадлежит ни одному из них, а любая точка ε>0 будет от-

делена от нуля полуинтервалом таким, что 1n <ε (ведь 1n →0 , как было показано выше).

44

На второй вопрос ответ даёт фундаментальная теорема Г. Кантора.

Теорема 1.3.10 (о вложенных отрезках «принцип Кантора»). Лю-

бая система An =[an , bn ] таких, что An+1 An , имеет общую точку. Если же lim(bn −an ) =0 , то точка единственна.

Доказательство. Из условия [an+1 , bn+1 ] [an , bn ] следует, что an ↑ и

ограничена сверху (хотя бы числом b1 ), а bn ↓ и ограничена снизу (хотя бы числом a1 ), но тогда по теореме о достаточных условиях сходимости последовательности существуют liman и limbn , которые обозначим a и b соответственно. Кроме того, поскольку an <bn , то по соответствующей тео-

применимо к нему. Насколько принципиально то, что в теореме Кантора фигурируют отрезки?

Выше мы видели, что всякая сходящаяся последовательность ограничена, т. е. ограниченность есть необходимое условие сходимости. Однако ограниченности xn не достаточно для сходимости. Очевидный пример:

xn =(−1)n – ограниченная, но не сходящаяся последовательность.

Как мы увидим ниже, во многих задачах не требуется сходимости самой последовательности – достаточно знать, что у неё существует сходящаяся подпоследовательность.

Определение 1.3.11. Число а называется частичным пределом по-

следовательности xn , если у неё существует подпоследовательность xn k , сходящаяся к а.

Например: xn =(−1)n nn+1 . Если n =2k , то

xn k = x2 k = 2k2k+1 =1 + 21k k →1.

Если n =2k −1, то

xn k = x2 k −1 = − 2k2k−1 = −1 −11(2k) k →−1.

Мы видим, что у данной xn есть, по крайней мере, два частичных предела, отличных друг от друга.

Вопрос. Может ли данная последовательность сходиться?

45

Более общий вопрос. Если у xn есть два различных частичных предела, может ли xn быть сходящейся?

Определение 1.3.12. Последовательность xn называется сходящейся к +∞ (−∞) , если

p R np N n >np : xn > p (xn < p) .

Теорема 1.3.11 (Больцано-Вейерштрасс). У любой ограниченной последовательности существует сходящаяся подпоследовательность. Если последовательность неограничена сверху (снизу), то неё существует сходящаяся к +∞ (−∞) подпоследовательность.

Доказательство. Второе утверждение почти очевидно. Действительно, неограниченность xn сверху означает, что

p R n p N : xn p > p .

Если в качестве p брать натуральные числа k =1, 2,..., то

k N nk N : xn k > k .

Очевидно, что выделенная таким образом xn k стремится к +∞.

Докажем теперь первое утверждение. Пусть xn ограничена, т. е. существует отрезок [a; b ] R такой, что

n N : xn [a; b ].

Разделим [a; b ] пополам точкой с. Тогда N разобьётся на два множества K1 и K2 таких, что K1 отображается в отрезок [a, c ], а K2 отображается в [c, b ]. Ясно, что хотя бы одно из этих множеств бесконечно. Вы-

берем то из двух множеств, которое бесконечно; любое из натуральных чисел этого множества обозначим n1 , а соответствующий этому множеству

отрезок обозначим [a1 , b1 ]. Ясно, что xn1 [a1 , b1 ]. Разделяя [a1 , b1 ] новой

точкой деления и повторяя рассуждения, мы получим натуральное число n2 и отрезок [a2 , b2 ] и т.д. Эта процедура не закончится на конечном шаге,

поскольку мы каждый раз выбираем бесконечное подмножество Ki . Итак, мы указали способ построения множества натуральных чисел

n1 , n2 ,..., nk ,... таких, что: xn k [ak ; bk ]; последовательность [ak ; bk ] –

вложенная и bk −ak =b2−ka <b −k a k→0 , следовательно, у всех [ak ; bk ] су-

ществует единственная общая точка ξ:

k N : ξ[ak ; bk ].

Но

k N : xn k [ak ; bk ],

следовательно,

46

Теорема доказана полностью.

Теорема Больцано-Вейерштрасса показывает, что у любой последовательности есть частичный предел, хотя бы бесконечный.

Определение 1.3.13. Наибольший частичный предел последователь-

меньший частичный предел называется нижним пределом и обозначается

lim xn .

n

Примем без доказательства следующую теорему.

Теорема 1.3.12. У любой последовательности есть как наибольший, так и наименьший пределы (хотя бы бесконечные), при этом для сходимо-

сти xn необходимо и достаточно, чтобы lim xn =lim xn .

n n

До сих пор мы говорили о сходимости последовательности, имея в виду, что существует некоторое число а, которое мы должны исследовать

– является ли оно пределом. Однако заранее это число может быть и неизвестным. Для «практического» исследования xn в этом случае годятся те правила вычисления пределов, о которых мы говорили выше, однако для теоретических исследований необходимо иметь такой инструмент исследования, который опирался бы только на свойства членов последовательности (на «внутренние свойства» последовательности) и не привлекал бы никаких «внешних» соображений таких, как заранее заданное число а.

С таким инструментом мы сейчас познакомимся.

Определение 1.3.14. Последовательность xn называется фундамен-

или, что тоже самое

ε>0 nε N n >nε m N : xn+m −xn <ε.

Теорема 1.3.13 (критерий Коши). Для того чтобы последовательность сходилась, необходимо и достаточно, чтобы она была фундаментальной.

Доказательство необходимости. Пусть xn →n a , то есть

ε>0 nε N n >nε : xn −a < 2ε .

Если теперь n, m >nε , то

xn −xm ≤ xn −a + a −xm < 2ε + 2ε =ε,

т. е. последовательность xn фундаментальна.

47

Доказательство достаточности. Пусть для xn выполняется (1.3.3).

Зафиксируем в условии (1.3.3) ε>0 (например, ε=1) и m0 >nε . Тогда

n >nε : xm0 −ε<xn <xm0 +ε,

т. е. xn ограничена. Выделим из неё сходящуюся подпоследовательность

В заключение этого раздела мы определим число е, которое иногда называют числом Непера.

Как мы увидим в дальнейшем, число е играет огромную роль в математическом анализе. Так, наиболее интересным логарифмом является логарифм по основанию е, а функция f (x) =ex – единственная функция, одна

из первообразых которой совпадает с ней самой. Теорема 1.3.14. Последовательность

n

xn = 1+ 1n

является сходящейся.

Доказательство. Покажем, что xn возрастает и ограничена сверху. Применим формулу бинома Ньютона:

Если, пользуясь этим выражением, записать xn+1 (формально это будет означать везде замену n на n+1), то мы увидим, что значение каждой из скобок увеличится:

1− kn <1− nk+1

48

и, кроме того, увеличится на единицу число слагаемых. Следовательно,

xn <xn+1 , т. е. xn ↑.

Чтобы доказать ограниченность, заметим, что

2k −1 = 2 2 2 . . . 2 < 2 3 . . . k = k!.

14243

k −1 раз

Заметим также, что для каждой из скобок имеет место неравенство

1−ni <1.

Осталось заметить, что справа стоит сумма членов убывающей геометрической прогрессии со знаменателем q =12 :

т. е. xn ≤3. Теорема доказана.

Относительно числа е известно, что оно является числом иррациональным и, следовательно, может быть вычислено приближённо (с точностью, которую допускают современные вычислительные средства).

Более того, число е является так называемым трансцендентным числом, т. е. не является корнем никакого многочлена с целыми коэффициентами.

Но раз уж мы заговорили о вычислении числа е, нужно отметить, что ни формула (1.3.4), ни, уж тем более, формула (1.3.5) непригодны для этой цели, поскольку, даже умея вычислить значения любого числа слагаемых в (1.3.4), мы не можем ответить на вопрос: какую ошибку (погрешность) мы допустим, вычисляя не предел (1.3.5), а некоторое значение (пусть и с большим номером) xn ?

На этот вопрос (и на другие подобные вопросы) мы научимся отвечать позже – когда изучим формулу Тейлора.

Определение 1.3.16. Натуральным логарифмом числа b >0 называ-

ется loge b , обозначаемый lnb .

В дальнейшем мы увидим, какую важную роль в анализе играет этот логарифм.

49

Вопросы для самопроверки.

1.Является ли множество иррациональных чисел счётным?

2.Будет ли противоречить данному выше определению счётного множества такое определенте: «счётным называется множество, равномощное множеству рациональных чисел интервала (0;1) ?»

3.Обязано ли быть счётным множество значений последовательности xn ?

4.Пусть xn строго возрастает. Будет ли счётным множество её значений?

5.Какие свойства xn определяют нижеследующие высказывания:

а) ε>0 nε N n >nε : xn −a <ε; б) ε>0 nε N n >nε : xn −a <ε; в) ε>0 nε N n >nε : xn −a >ε;

г) a R ε>0 nε N n >nε : xn −a ≥ε;

д) a R ε>0 nε R n >nε : xn −a <ε?

6. Будет ли сходиться к +∞ всякая неограниченная сверху последовательность?

7.Будет ли последовательность, сходящаяся к +∞, неограничена сверху?

8.Справедливо ли равенство (ответ обоснуйте):

Ответы.

1. Нет (попробуйте предположить противное). 2. Нет. 3. Нет, например, постоянная xn . 4. Да. 5. а) xn ограничена; б) существует ограниченная подпоследовательность; в) xn не сходится к числу а; г) xn не сходится ни к какому числу; д) у xn существует сходящаяся подпоследовательность. 6. Нет. 7. Да. 8. Да.

Упражнение 1.3.

1. Выяснить, какие из нижеперечисленных множеств могут быть конечными, счётными, несчётными.

а) Множество всех конечных последовательностей натуральных чисел.

б) Множество всех прямых на плоскости. в) Множество непесекающихся интервалов.

г) Множество всех корней всех ненулевых многочленов с целыми коэффициентами.

д*) Множество кругов на плоскости, имеющих рациональный радиус и центр в точке с рациональными координатами. (Как изменится ответ, если круги на плоскости заменить шарами в пространстве.)

50