Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Zabotin_Dulliev_Chernyaev_-_Mat_an

.pdf

Скачиваний:

Добавлен:

22.03.2016

Размер:

3.78 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1513 14 15 > Следующая >>>

A R : x

→x

f (x) − f (x0 )

→A

x −x0

Что оно означает?

4. Пусть f (x) =esin x . Какая из записей

df (x) =esin x d (sin x) и df (x) =esin x cos x dx

верна?

f (x) =

5. Пусть на отрезке [−1;1] задана

. Убедитесь, что у неё нет

стационарной точки, хотя f (−1) = f (1) . Почему утверждение теоремы Ролля здесь не имеет места?

6. Пусть f такова, что f // (x0 ) =0 , f /// (x0 ) ≠0 . Что можно сказать о точке x0 ?

7. Какой физический смысл имеет f // (x) ?
8. В силу первого правила Лопиталя limsin x		=cos x	=1. Можно ли

x→0	x	1	x=0

эти рассуждения считать доказательством первого замечательного предела?

9. Имеет ли смысл при построении графика функции

	x		−x		x 2
f (x) =e		+e		+cos x
f (x) =e		+e		+cos x
					1− x

исследовать вопрос о её чётности (нечётности)?

10. Может ли график функции пересекаться с наклонной асимпто-

той? (Рассмотрите пример f (x) =x2 sin x .)
Ответы.
1. Как видно из примера, f	не дифференцируема ни в какой точке
x ≠0 в силу разрывности. Однако	f / (0) =0 .

2.A= f / (x0 ) – записано определение f / (x0 ) по Коши.

3.A= f / (x0 ) – записано определение f / (x0 ) по Гейне.

4.Обе.

5.В точке x0 =0 не существует f / (x0 ) , т. е. одно из условий теоремы

Ролля не выполнено.

6.Точка x0 – точка перегиба графика f .

7.Ускорение.

8.Нет, поскольку формула (sin x)/ =cos x получена с применением

первого замечательного предела.

9. Нет, поскольку D( f ) несимметрична относительно нуля и проверка условий типа f (−1) = f (1) не имеет смысла: f (−1) существует, а f (1) – нет.

10. Да. Причём сколько угодно раз. Это видно из примера.

121

Упражнение 1.6

Решение типовых задач

1. Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции y = x .

Решение. Находим приращение функции:

y = x +

x − x . Отсюда

y =

x + x − x

и lim

= lim

x +

x −

x→0 x

x→0

Таким образом,

(

x +

x −

x)(

x +

y/ = lim

x( x + x + x)

x→0

= lim

x +

x −x

= lim

x( x + x −

x + x +

2 x

x→0

Итак, y/ =

2. Применяя формулы и правила дифференцирования, найти производную функции y =x x (3ln x −2) .

Решение. Перепишем заданную функцию в виде

y =x3/2 (3ln x −2) .

Тогда y

/ =x3/2 3 +

3 x1/2

(3ln x −2) =3x1/2

+ 9 x1/2 ln x −3x1/2 =

x ln x .

3. Найти производную функции y =(2x3 +5)4 .

Решение. Обозначим 2x3 +5=u , тогда y =u4 . По правилу дифферен-

цирования сложной функции имеем

y/ =(u4 )u/ (2x3 +5)/x =4u3 (6x2 ) =24x2 (2x3 +5)3 .

4. Найти производную функции y =

sin x

+ln1+sin x .

cos2 x

cos x

Решение. Преобразуем данную функцию:

y =

sin x

+ln(1+sin x) −ln cos x .

Тогда

cos2 x

=cos2 x cos x −sin x 2cos x (−sin x) +

cos x −

(−sin x) ,

1+sin x

cos x

или

cos4 x

cos2 x +2sin 2 x

cos x (1−sin x)

sin x

cos

2 x +2sin 2 x

1−sin x

y/ =

cos3 x

1−sin 2 x

cos x

cos3 x

cos x

+ sin x

=cos2 x +2sin 2 x +

cos x

cos3 x

cos x

cos3 x

5. Найти производную функции y =(sin x)tg x .

Решение. Здесь основание и показатель степени зависят от х. Логарифмируя, получим ln y =tg x ln sin x . Продифференцируем обе части по-

122

следнего равенства по х. Так как у является функцией от х, то ln y

есть

сложная функция х и (ln y)/ =

y/ . Следовательно,

=tg x

cos x +

ln sin x

=1+ln sin x ;

sin x

cos2 x

= y

ln sin x

=(sin x)

tg x

ln sin x

cos2

cos2 x

6. Найти dy

, если x =t3 +3t +1, y =3t5 +5t3 +1.

dy =15t 4 +15t 2 . Следовательно,

Решение. Найдём

=3t 2 +3 ,

15t

4 +15t 2

=5t

3t 2 +3

7. Какой угол α образует с осью

абсцисс касательная

кривой

y =(2/3) x5 −(1/9) x3 , проведённая в точке с абсциссой x =1?

Решение. Находим

производную

y/ =(10/3) x4 −(1/3) x2 .

При

x =1

имеем y/ =3 , т. е. tg α=3 , откуда α=arctg 3≈71034/ .

8. Дана функция y =2x . Найти y(n) .

Решение. Имеем

y/ =2x ln 2 , y// =2x ln2 2 ,

y/// =2x ln3 2 , ... , y(n) =2x lnn 2 .

9. Найти дифференциал функции y =ctg x .

Решение. Имеем dy =(ctg x)/ dx =−

sin 2 x

10. Найти дифференциалы первого, второго и третьего порядков

функции y =(2x −3)3 .

Решение. Имеем

dy =3(2x −3)2 2dx =6(2x −3)2 dx ,

d 2 y =12(2x −3) 2dx2 =24(2x −3) dx2 ,

d 3 y =24 2dx3 =48dx3 .

11. Вычислить приближённое значение arcsin 0,51.

Решение. Рассмотрим функцию y =arcsin x . Полагая x =0,5,

x =0,01

и применяя формулу arcsin(x +

x) ≈arcsin x +(arcsin x)/

x , получаем

arcsin 0,51≈arcsin 0,5+

0,01= π+0,011≈0,513 .

1−(0,5)2

12. Выполняется ли теорема Ролля для функции

f (x) =x2 −6x +100 ,

если a =1, b =5? Если да, то при каком значении ξ?

Решение. Так как функция

f (x)

непрерывна и дифференцируема

при всех х и f (1) = f (5) =95, то теорема Ролля на этом отрезке выполняется. Значение ξ определяем из уравнения f / (x) =2x −6 =0 , т. е. ξ=3.

123

13. На дуге АВ кривой y =2x −x2 найти точку М, в которой касательная параллельна хорде АВ, если A(1;1) и B(3;−3) .

Решение. Функция y =2x −x2 непрерывна и дифференцируема при

всех х. По теореме Лагранжа между двумя значениями a =1 и b =3 существует значение x =ξ, удовлетворяющее равенству

y(b) − y(a) =(b −a) y/ (ξ) ,

где y/ =2 −2x . Подставив соответствующие значения, получим

y(3) − y(1) =(3−1) y/ (ξ) ; (2 3−32 ) −(2 1−12 ) =(3−1) (2 −2ξ) ; −4 =4(1−ξ) .

Отсюда ξ=2 ,

y(2) =0 . Таким образом, точка М имеет координаты (2; 0) .

14. Представить функцию f (x) =3 x

в виде многочлена пятой степе-

ни относительно двучлена x −1.

f (x) =x1/3

Решение. Вычислим значения функции

и её производных

до пятого порядка включительно при x0 =1:

f (1) =1, f / (x) =(1/3) x−2/3 , f / (1) =1/3;

f // (x) =−(2/9) x−5/3 ,

f // (1) =−2/9 ;

f /// (x) =(10/ 27) x−8/3 ,

f /// (1) =10/ 27 , f IV (x) =−(80/81) x−11/3 ,

f IV (1) =−80/81,

f V (x) =(880/ 243) x−14/3 , f V (1) =880/ 243 .

Следовательно, по формуле Тейлора получим

3 x =1+1(x −1) −

(x −1)2 +

(x −1)3 −

(x −1)4

880

(x −1)5 +R5 ,

81 4!

243 5!

27 3!

где R5 =

f IV (ξ)

(x −1)6 =−12320 ξ−17/3

(x −1)6

, 1<ξ<x .

729 6!

15. Используя правило Лопиталя, вычислить предел lim

x −sin x

x→0

Решение. Имеем неопределённость вида 0/0. Получаем

lim

−sin x

=lim

1−cos x

=lim

sin x

=lim

cos x

3x2

x→0

Здесь правило Лопиталя применено трижды.

16. Вычислить предел lim x2 .
x→∞ ex
Решение. Имеем неопределённость вида ∞/∞. Применяя правило
Лопиталя два раза, получим: lim x2	=lim 2x =lim 2	=0 .
x→∞ ex	x→∞ ex x→∞ ex

17. Вычислить предел lim (x2 ln x) .

x→0

Решение. Имеем неопределённость вида 0 ∞ . Представив произведение в виде частного, а затем, получив неопределённость вида ∞/∞, применим правило Лопиталя:

lim (x2 ln x) =lim		ln x	=lim			1 x	=−1 lim x2	=0 .
lim (x2 ln x) =lim		1 x2	=lim		−2 x3		=−1 lim x2	=0 .
x→0	x→0	1 x2		x→0	−2 x3		2 x→0
		1		1
18. Вычислить предел lim			−			.
18. Вычислить предел lim			−			.
	x→0 x			ex −1

124

Решение. Имеем неопределённость вида ∞−∞. Приведём дроби к общему знаменателю, а затем, получив неопределённость вида 0/0, применим правило Лопиталя:

lim ex −1−x	=lim	ex −1	=lim	ex	=1 .

x→0 x(ex −1)	x→0 ex −1+xex		x→0 ex (2 +x)		2

19. Вычислить предел lim (sin x)x .

x→0

Решение. Имеем неопределённость вида 00 . Обозначим (sin x)x = y и

прологарифмируем её:

ln y =x ln sin x =ln sin x . 1/ x

Вычислим предел ln y , применяя правило Лопиталя (здесь имеем неопределённость вида ∞/∞):

lim ln y =lim ln sin x			=lim cos x/sin x =
x→0	x→0	1/ x	x→0	−1 x2
	x2 cos x				x
=−lim		=−lim x cos x				=0 .
=−lim	sin x	=−lim x cos x			sin x	=0 .
x→0	sin x	x→0			sin x
Следовательно, lim y =e0	=1.
x→0

20. Вычислить предел lim(1+x)ln x .

x→0

Решение. Имеем неопределённость вида 1∞ . Обозначив данную функцию через у, логарифмируя и применяя правило Лопиталя, получим

lim ln y =lim (ln x ln (1+x)) =lim ln(1+x) =
x→0	x→0			x→0 1/ln x
=lim	1 (1+x)	=−lim	xln2 x	=−lim		ln2 x		=
						1+1/ x
x→0 −1 (xln2 x)		x→0 x +1		x→0
=−lim (2ln x) x		=2lim ln x =2lim			1	x	=0 .
					−1	x2
x→0	−1 x2	x→0 1/ x		x→0

Таким образом, lim y =e0 =1.

x→0

21. Найти интервалы возрастания и убывания функции y =x −2sin x , если 0≤x≤2π.

Решение. Находим производную: y/ =1−2cos x . Очевидно, что y/ =0 в интервале (π/3; 5π/3) y/ <0 в интервалах (0; π/3) и (5π/3; 2π) . Таким образом, в интервале (π/3; 5π/3) данная функция возрастает, а в интервалах

(0; π/3) и (5π/3; 2π) - убывает.
22. Исследовать на экстремум функцию y =(x −1)4 .
Решение. Находим производную:	y/ =4(x −1)3 . Из условия y/ =0		на-
ходим стационарную точку x =1. Вторая производная		y// =12(x −1)2	при
x =1 равна нулю. Третья производная	y/// =24(x −1) при	x =1 также обра-

125

щается в нуль. Четвёртая производная yIV =24 >0 . Следовательно, в точке x =1 функция имеет минимум ymin =0 .

23. Найти наибольшее и наименьшее значения функции f (x) =3x −x3 на отрезке [−2; 3].

Решение. Находим производную: f / (x) =3−3x2 . При x =±1 имеем f / (x) =0 , т. е. x =±1 - стационарные точки. Определяем значения функции в этих точках: f (1) =2 , f (−1) =−2 . Вычисляем значения данной функции на границах промежутка: f (−2) =2 , f (3) =−18. Из полученных четырёх

значений выбираем наибольшее и наименьшее. Итак, наибольшее значение функции на данном отрезке равно 2, а наименьшее равно −18 .

24. Найти промежутки выпуклости и вогнутости и точки перегиба графика функции y =x5 +5x −6 .

Решение. Имеем y/ =5x4 +5 , y// =20x3 . Если x<0 , то y// <0 и кривая выпукла; если же x >0 , то y// >0 и кривая вогнута. Слева от точки x =0

кривая выпукла, справа – вогнута; следовательно, точка с абсциссой x =0 является точкой перегиба; значение функции при x =0 равно −6 . Итак, кривая выпукла в промежутке (−∞; 0) и вогнута в промежутке (0;+∞) , а

точка (0;−6) является точкой перегиба.

25. Найти асимптоты кривой y =x +2arctg x .

Решение. Вертикальных асимптот кривая не имеет, поскольку ни при каком конечном значении а пределы

lim (x +2arctg x) и lim (x +2arctg x)
x↑a	x↓a

не являются бесконечными. Горизонтальных асимптот кривая также не имеет, поскольку

lim (x +2arctg x)	и lim (x +2arctg x)
x→+∞	x→−∞

не являются конечными величинами. Ищем наклонные асимптоты:

	1) k1 = lim	x +2arctg x			2arctg x
				= lim 1+	x		=1;
			x	= lim 1+			=1;
	x→+∞		x	x→+∞
b1	= lim (x +2arctg x −x) =2(π/ 2) =π; y =x +π - правая асимптота;
	x→+∞		x +2arctg x		2arctg x
	2) k2 = lim		x +2arctg x		2arctg x
				= lim 1+			=1;
			x	= lim 1+	x		=1;
	x→−∞		x	x→−∞	x
b1	= lim (x +2arctg x −x) =2(−π/ 2) =−π; y =x −π - левая асимптота.
	x→−∞
	26. Найти асимптоты кривой y =x2ex .
	Решение.	Вертикальных асимптот,				очевидно, нет. Если x→∞, то

y →0 . Следовательно, ось Ох является горизонтальной асимптотой данной кривой. Определим, существует ли наклонная асимптота:

k =lim	x2e−x	=lim	x	=lim	1	=0 .
	x
x→∞		x→∞ ex		x→∞ ex

Таким образом, имеется только горизонтальная асимптота y =0 .

126

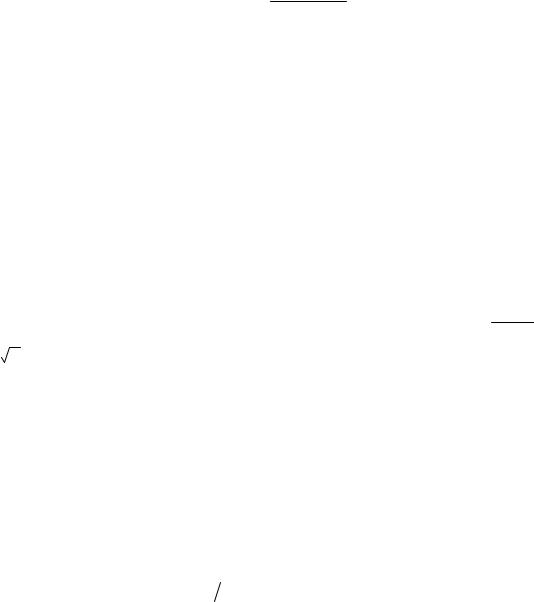
27.Найти асимптоты кривой y = x2 −2x +3 .

x+2

Решение. Если x→−2 , то y →∞, т. е. x =−2 - вертикальная асимптота. Найдём невертикальные асимптоты:

k =lim	x2 −2x +3	=1, b =lim		x2 −2x +3	−x =−4 .

	x(x +2)
x→∞		x→∞	x +2

Таким образом, наклонная асимптота имеет уравнение y =x −4 .
28. Провести полное исследование функции y =						x3 +4	и построить её

график. Решение.

1)Область определения функции - вся ось Ох, за исключением точки

x=0 , т. е. D( y) =(−∞; 0)U(0;+∞) .

2)Функция не является чётной или нечётной.

3) Найдём точки пересечения графика с осью Ох: имеем

x =−3 4 .

4) Точка разрыва x =0 , причём			lim y =∞				; следовательно,
			x→0
Оу) является вертикальной асимптотой графика.
Найдём наклонные асимптоты:
k =lim	f (x)	=lim		x3 +4		=1;
	x			x3
x→∞		x→∞
		x3 +4						4
b =lim[f (x) −kx]=lim					−x		=lim		=0 .
			x2
x→∞	x→∞						x→∞ x2

x3x+2 4 =0 ;

x =0 (ось

Наклонная асимптота имеет уравнение y =x .

5) Найдём экстремумы функции и интервалы возрастания и убыва-


ния. Имеем y/ =1−8/ x3 =(x3 −8)		x3 ; y/	=0 при x =2 ; y/ =∞ при x =0 (точка
разрыва функции). Точки x =0		и x =2	разбивают числовую ось на проме-
жутки	(−∞; 0) , (0; 2) и (2;+∞) , причём y/ >0 в промежутках (−∞; 0) и
(2;+∞)	(функция возрастает) и y/ <0 в промежутке (0; 2)			(функция убыва-
ет). Далее, находим y// =24/ x4 ;		y// (2) >0 . Следовательно,		x =2 - точка ми-

нимума, ymin =3 .

6) Найдём интервалы выпуклости и вогнутости кривой и точки её перегиба. Так как y// >0 , то график функции всюду вогнут. Точек перегиба

кривая не имеет.

Используя полученные данные, строим график функции.

127

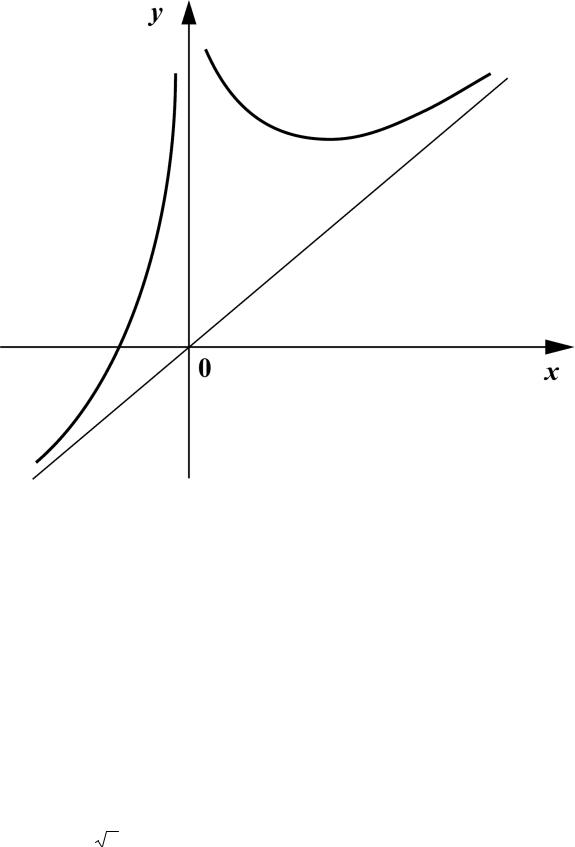
Задачи для самостоятельного решения Группа А

Приращение функции. Определение производной

1. Найти приращение функции y =x3 в точке x0 =2 , полагая прира-

щение	x равным: 1) 2; 2) 1; 3) 0,5; 4) 0,1.
2. Найти отношение			y для функций:
			x
1)	y =2x3 −x2 +1 при x =1;			x =0,1;
2)	y =1	при x =2 ;	x =0, 01;
	x	x при x =4 ;	x =0, 4 .
3)	y =
Показать, что при			x→0	предел этого отношения в первом случае

равен 4, во втором равен −0, 25 , в третьем равен 0, 25 .

128

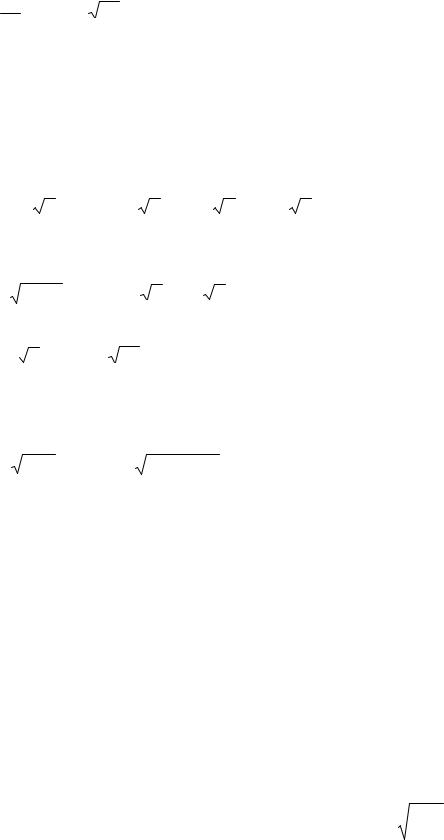
3. Дана функция y =x2 . Найти приближённые значения её производной в точке x =3, полагая последовательно x равным: 1) 0,5; 2) 0,1; 3)

0,01; 4) 0,001.

В задачах 4–7 найти производные функций, исходя из определения производной (не пользуясь формулами дифференцирования).

4. y = x12 . 5. y =3 x2 . 6. y =2x3 +5x2 −7x −4 . 7. y =−x −ctg x .

Дифференцирование степенных функций

В задачах 8–28 найти производные данных функций, применяя формулы и правила дифференцирования.

8. y =3x2 −5x +1.										9. y =2x3 −5x2 +7x +4 . 10.																					y =			7		.
8. y =3x2 −5x +1.										9. y =2x3 −5x2 +7x +4 . 10.																					y =					.
		3 x3										2 x3					4										2							x3
11.	y =				x .				12.						x −		4			x5			x +				2		x7	x .	13. y =(2x3 +5)4 .
11.	y =				x .				12.						x −					x5			x +		15				x7	x .	13. y =(2x3 +5)4 .
		4										7				11									15														5
	y =	(5x		3	+x			2			5											2		4					6							1+x2			5
14.									−4)				. 15. y =							7x			−	x		+6 .				16.		y =							.
14.									−4)				. 15. y =							7x			−			+6 .				16.		y =							.
																																				1+x
17.	y =	1−x2 .							18.				y =		x (x3 −							x +1) .
19.	y =(x2 −3x +3)(x2 +2x −1) .																				20.		y =(x3 −3x +2)(x4 +x2 −1) .
21.	y =(3 x +2x)(1+3 x2 +3x) .																				22.		y =						x	. 23.			y =				1−x3	.
21.	y =(3 x +2x)(1+3 x2 +3x) .																				22.		y =					x2 +1		. 23.			y =					.
		2												x2 +x −1														x2 +1		2						1+x3
24.	y =					. 25.				y =				x2 +x −1						.	26.			y =											.
24.	y =					. 25.				y =										.	26.			y =											.
		x3 −1													x3 +1														(x2 −x +1)2
27.	y =	1+x					.		28.			y =				1							.
		1−x													1−x4 −x8
29.	y(x) =(x2 +x +2)3/2 ; найти y/ (1) .
30.	y(x) =		x +1						1/2	; найти y						/	(2) .


			x −1
31.	y(x) =				1−x2 1/2							; найти y						/	(0) .
31.	y(x) =											; найти y							(0) .
			1+x2

Дифференцирование тригонометрических

иобратных тригонометрических функций

Взадачах 32–52 найти производные данных функций, применяя формулы и правила дифференцирования.

32.	y =sin x +cos x . 33. y =			tg x	.	34. y =cos2 x .	35.	y =sin(2x +3) .

		1		x						x
36.	y =sin		. 37. y =sin(sin x) .			38. y =cos3 4x .	39.	y =	tg		.
										2
		x

129

40.

y =ctg 3 1+x2 .

41. y =sin 2 (cos 3x) .

42. y =xarcsin x .

43.

y = x arctg x .

44. y =

arccos x

45.

y =arcsin 2 .

46.

y =arctg2 1 .

47.

y =arctg(x2 −3x +2) .

48. y =3cos2 x −cos3 x .

49.

y =sin 2

ctg

50.

y =arcsin sin x . 51.

y =arccos

1−3x . 52.

y =arctg

1−x

1+x

Дифференцирование логарифмических, показательных

игиперболических функций

Взадачах 53–82 найти производные данных функций, применяя формулы и правила дифференцирования.

53.

y =ln2 x .

54. y =x2 log3 x .

55.

y =xlg x . 56. y =

ln x .

57.

y =ln(x2 +5) .

58. y =

ln x

59. y =

1+ln2 x . 60. y =ln sin x .

1+x2

61.

y =log3 (x2 −1) .

62. y =ln arccos 2x .

63. y =arctg[ln(3x +5)] .

64.

y =10x . 65. y =x 10x .

66. y =xex . 67. y =ex cos x .

68.

y =

69.

y =e x+1 .

70.

y =3sin x .

71. y =earcsin 2 x .

1+x2

73. y =ln ch x .

y =arctg(th x) . 75.

y =ch(sh x) .

72.

y =sh3 x .

74.

76.

y =xsh x −ch x .

77. y =xarcsin(ln x) .

78. y =x 10

x .

79.

y =xe1−cos x . 80. y =ln(ex cos x +e−x sin x) .

81.

y =ln tg

−ctg x ln(1+sin x) −x .

82. xex arctg x .

ln5 x

83.

Показать,

что функция

y =ln

удовлетворяет соотношению

1+x

xy/ +1=ey .

84. Показать, что функция y =arcsin1−x2x удовлетворяет соотношению

(1−x2 ) y/ −xy =1.

Логарифмическое дифференцирование

В задачах 85–95 найти производные данных функций, используя правило логарифмического дифференцирования.

85. y =xx2 . 86. y =(ln x)x . 87. y =(sin x)cos x . 88. y =(x +1)2/ x .

	ln x		1/ x			sin x				x x
89. y =x		. 90. y =x		.	91. y =x		.	92.	y =		.
89. y =x		. 90. y =x		.	91. y =x		.	92.	y =		.
										1+x

130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1513 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.12.2018288.77 Кб4We ОЭЗ.doc
#
17.12.2018226.82 Кб2WE Платежный баланс.doc
#
11.11.2019438.78 Кб4What Are Polymers 1st Edition.doc
#
12.03.2015822.78 Кб66XX1-33.doc
#
12.03.2015117.25 Кб5xyushke.doc
#
22.03.20163.78 Mб87Zabotin_Dulliev_Chernyaev_-_Mat_an.pdf
#
12.03.2015890.37 Кб31Zadachi_srednie_2014_srednie.doc
#
12.03.20151.2 Mб12Zadachi_uslozhnyonnye_2014_80.doc
#
12.03.20154.31 Mб127Zaripov MJG.docx
#
23.05.20151.18 Mб38Zinnatullina_G_F_Posobie_2010.doc
#
10.11.2019626.69 Кб5zo.econ.audit_umk аудит.doc