
Zabotin_Dulliev_Chernyaev_-_Mat_an
.pdf
Доказательство очевидно следует из определения предела функции по Коши:
|
~ |
~ |
(x0 ): c −ε< f (x) <c +ε, |
|
|
ε>0 Uδ1 |
(x0 ) x Uδ1 |
|
|
т. е. |
~ |
|
|
|
f ограничена в Uδ1 (x0 ) . |
|
|
||
|
Теорема 1.4.6. Если существуют пределы a =lim f (x) |
и b=lim g(x) , |
||
|
|
|
x→x0 |
x→x0 |
то существуют пределы
lim( f (x) ±g(x)) =a ±b ;
x→x0
lim f (x) g(x) =a b ;
x→x0
lim f (x) = a – в последнем случае предполагается, что b ≠0 .
x→x0 g(x) b
Доказательство следует из определения Гейне и соответствующих свойств пределов числовых последовательностей.
~
Теорема 1.4.7. Если f (x) ≡c в Uδ (x0 ) , то lim f (x) =c .
x→x0
|
Доказательство следует из определения, например, Коши. |
|
|||||
|
Теорема 1.4.8. Если существуют |
a =lim f (x) |
и |
b=lim g(x) |
и при |
||
|
|
~ |
~ |
x→x0 |
|
x→x0 |
|
|
|
такая, что |
|
|
|
||
этом a >b, то найдётся U |
δ1 (x0 ) Uδ (x0 ) |
|
|
|
|||
|
|
|
~ |
|
|
|
|
|
Доказательство. |
x Uδ1 (x0 ): f (x) >g(x) . |
|
|
|
||
|
По лемме об отделимости найдутся окрестности |
||||||
Uε (a) и Uε (b) такие, что Uε (a) >Uε (b) , |
|
|
~ |
такая, |
|||
но тогда найдётся Uδ1 (x0 ) |
|||||||
|
~ |
|
|
|
|
|
|
что x Uδ1 (x0 ) выполняются одновременно условия: |
|
|
|||||
|
|
f (x) Uε (a), f ( y) Uε (b) , |
|
|
|
||
т. е. |
f (x) >g(x) , что и требовалось. |
|
|
|
|
||
|
Следствие. Если lim f (x) >c ≡const , то |
|
|
|
|||
|
|
x→x0 |
~ |
|
|
|
|
|
|
~ |
|
|
|
|
|
|
Uδ1 |
(x0 ) x Uδ1 (x0 ): f (x) >c . |
|
|
|
||
|
Доказательство |
очевидно, если |
взять g(x) ≡c |
и воспользоваться |
|||
теоремой 1.4.7. |
|
|
|
|
|
|
|
|
Теорема 1.4.9. Если существуют |
a =lim f (x) |
и |
b=lim g(x) |
и при |
||
|
~ |
|
|
x→x0 |
|
x→x0 |
|
|
|
|
~ |
≥g(x) , то a≥b . |
|
||
этом Uδ1 (x0 ) Uδ (x0 ) |
такая, что x Uδ1 (x0 ): f (x) |
|
|||||
|
Доказательство. Пусть справедливо обратное: a<b , тогда по пре- |
||||||
дыдущей теореме в некоторой окрестности точки x0 |
выполнится неравен- |
||||||
ство |
f (x) <g(x) , что противоречит предположению теоремы. |
|
|||||
|
Теорема 1.4.10. |
|
~ |
|
|
|
этом |
|
Если x Uδ (x0 ): f (x)≤ϕ(x) ≤g(x) и при |
||||||
lim f (x) =lim g(x) =a , то lim ϕ(x) =a . |
|
|
|
|
|||
x→x0 |
x→x0 |
|
x→x0 |
|
|
|
|
Доказательство. Возьмём xn →n x0 . Тогда f (xn ) ≤ϕ(xn ) ≤g(xn ) . Пе-
реходя к пределу и используя теорему о сжимающих последовательностях,
61
получим lim ϕ(xn ) =a , и, поскольку xn выбрана произвольно, теорема до-
n
казана в силу определения Гейне.
Замечание. Последние три теоремы называют теоремами о предельных переходах в неравенствах.
Для функций, монотонных на конечном или бесконечном интервале (a; b) , справедливы теоремы о существовании пределов. Докажем одну из
них: |
|
|
|
|
|
||
Теорема 1.4.11. Если f монотонна на интервале (a; b) |
и ограничена |
||||||
на нём, то существуют конечные пределы lim f (x) и lim f (x) . |
|||||||
|
|
x↑b |
f |
x↓a |
|
||
Доказательство. Пусть для определённости |
монотонно возраста- |
||||||
ет и ограничена. Пусть S = sup f (x) , тогда |
|
|
|
|
|
||
x (a;b) |
|
|
|
|
|
||
1) x (a; b): f (x)≤S ; 2) ε>0 xε (a; b): f (xε ) >S −ε. |
|
||||||
Но f возрастает, следовательно, |
|
|
|
|
|
||
x (xε ; b): f (x)≥ f (xε ) >S −ε, |
|
|
|||||
таким образом |
|
|
|
|
|
||
ε>0 δ=xε x (δ; b): |
|
f (x) −S |
|
<ε, |
|
||
|
|
|
|||||
т. е. S =lim f (x) , что и требовалось. |
|
|
|
|
|
||
x→b |
f |
(x) = inf |
f (x) . |
||||
Аналогично доказывается существование lim |
|||||||
|
|
x→a |
|
|
|
x (a;b) |
|
Определение 1.4.4. Функция α называется бесконечно малой вблизи
точки x0 , если lim α(x) =0 .
x→x0
Теорема 1.4.12. Число с будет являться пределом функции f в точке x0 тогда и только тогда, когда найдётся бесконечно малая вблизи x0
~
функция α такая, что для всех x Uδ (x0 ) выполнится равенство f (x) =c +α(x) .
Доказательство. Пусть с=lim f (x) . Тогда положим α(x) = f (x) −c .
x→x0
Очевидно, lim α(x) =lim ( f (x) −c) =0 , т. е. искомая α(x) построена.
x→x0 x→x0
Обратно, если существуют такие с и α(x) , что f (x) =c +α(x) , то у
правой части этого равенства существует предел lim(c +α(x)) =c , а значит,
x→x0
существует предел lim f (x) =c . Теорема доказана.
x→x0
Упражнение. С помощью теоремы 1.4.12 доказать теорему 1.4.6. По существу теорема 1.4.12 показывает, что определение предела
функции в точке мы могли бы дать, если бы сначала ввели понятие бесконечно малой функции. Действительно, это можно было сделать так: число с называется пределом функции f в точке x0 , если функция f (x) −c явля-
ется бесконечно малой вблизи точки x0 .
Это замечание показывает, насколько важным является понятие бесконечно малой функции.
62

Нам в дальнейшем неоднократно придётся выяснять вопрос: какая из двух данных нам бесконечно малых вблизи x0 функций α и β стремится к нулю быстрее?
Для этого надо договориться о том, как мы будем понимать слово «быстрее».
Введём следующие понятия:
– если существует lim α(x) = p ≠0 , то будем говорить, что α и β име-
x→x0 β(x)
ют одинаковый порядок малости;
– если при этом p =1, то α и β назовём эквивалентными вблизи x0 и
будем это обозначать так: α(x) ~ β(x) ;
x→x0
– если lim α(x) =0 , то будем говорить, что α имеет больший порядок
x→x0 β(x)
малости, нежели β, и будем обозначать это так: α = o (β) ;
–если α = o (β) и найдётся натуральное число k такое, что функции
αи βk будут одного порядка малости, то будем говорить, что α имеет k-й порядок малости относительно функции β.
В заключение этого раздела докажем две теоремы о пределах, назы-
ваемых замечательными пределами.
Первый замечательный предел.
|
lim |
sin x |
=1 |
||||
|
|
||||||
или, что то же самое |
x→0 |
x |
|
|
|||
sin x ~ |
x . |
||||||
|
|||||||
Доказательство. Покажем, что |
x→0 |
|
|
||||
|
|
|
|||||
lim |
sin x |
=lim |
sin x |
||||
|
|
||||||
x↑0 |
x |
x↓0 |
|
x |
|||
Для того чтобы доказать равенство lim sin x
x↓0 x
тригонометрическим кругом:
(1.4.6)
=1.
=1, воспользуемся единичным
63
Из рисунка ясно, что площадь треугольника OBA меньше площади кругового сектора OBA, которая, в свою очередь, меньше площади треугольника OCA , т. е.
12 OB OA sin x<12 OB OA x<12 OA CA.
Учитывая, что OB =OA=1, CA=tg x , имеем |
|
|||||
sin x<x<tg x , |
(1.4.7) |
|||||
или, учитывая, что sin x >0 при x (0; π) , |
|
|
|
|||
1< |
x |
< |
1 |
. |
(1.4.8) |
|
sin x |
cos x |
|||||
|
|
|
|
|||
Нам остаётся показать, что cos x x x→1. Для этого, используя эле-
→ 0
ментарную тригонометрическую формулу и левое неравенство из (1.4.7), запишем:
|
|
|
1−cos x |
|
2 x |
x |
2 |
1 |
x |
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
=2sin |
|
|
<2 |
|
|
= |
|
|
→0 . |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
x→0 |
|
|
|||
|
|
|
|
|
|
|
|
|
x |
|
|||||||
Переходя к пределу в (1.4.8) при x↓0 , мы и получаем lim |
=1, что, ра- |
||||||||||||||||
sin x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x↓x0 |
|
||
зумеется, равносильно утверждению |
|
x ~ sin x |
или, что |
то |
же самое, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
x↓0 |
|
|
|
|
|
|
|
lim |
sin x |
=1. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x↓0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Если теперь x<0 и вновь |
рассматривается предельный переход |
|||||||||||||||
lim sin x , то, очевидно, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x↑0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
sin x =sin(−x) =sint →1. |
|
|
||||||||||||
|
|
|
x |
−x |
|
t |
t↓0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Равенство (1.4.6) полностью доказано.
Второй замечательный предел.
Выше мы ввели в рассмотрение число е как предел специальной по-
def |
|
1 n |
|
|
|
следовательности: e =lim 1+ |
. |
|
|
|
|
n |
|
n |
существовать предел при x→+∞ у |
||
Возникает вопрос: |
будет ли |
||||
функции более общего вида |
|
|
1 |
x |
|
f (x) = 1+ |
x |
, и если он существует, то чему |
|||
|
|
|
|
|
|
он равен?
Надо ожидать, что если этот предел существует, то он равен числу е, что следует из определения самого числа е и определения предела функции по Гейне.
64

Ниже мы докажем, что |
|
1 x |
|
|
|
|
(1.4.9) |
||
lim 1+ |
|
=e |
||
x→+∞ |
|
x |
|
|
и, более того, |
|
x |
|
|
|
1 |
|
(1.4.10) |
|
lim 1+ |
x |
=e , |
||
x→−∞ |
|
|
|
|
но сначала напомним определение целой части числа: целое число E(x) называется целой частью числа х, если:
1)E(x)≤x ;
2)E(x) +1>x .
Например: E(1, 51) =1, E(7) =7, E(−2, 3) =−3 . Иными словами, целая
часть числа х – это ближайшее к х слева целое число.
Доказательство формулы (1.4.9) проведём с помощью определения Гейне. Возьмём произвольную последовательность xn ↑+∞. Ясно, что начиная с некоторого номера xn >0 , поэтому kn =E(xn ) можно считать нату-
ральными числами. Очевидно, из определения целой части kn ≤xn ≤kn +1,
откуда
1+ < 1 ≤ 1 , kn 1 xn kn
откуда, в свою очередь,
|
|
|
1 |
|
+1< |
1 |
+1≤ |
1 |
+1. |
||||
|
|
|
kn +1 |
|
|
||||||||
|
|
|
|
|
xn |
kn |
|
||||||
Но тогда с учётом (1.4.11) |
|
|
|
|
|
|
|
|
|
||||
1 |
kn |
1 |
|
xn |
1 |
kn +1 |
|||||||
|
|
|
+1 |
< |
|
+1 |
≤ |
|
+1 . |
||||
|
|
|
|||||||||||
kn +1 |
|
xn |
|
|
kn |
|
|||||||
(1.4.11)
(1.4.12)
Простейшими преобразованиями эти неравенства можно записать в
виде: |
|
|
|
kn +1 |
|
|
|
|
|
|
|
|
−1 |
|
|
|
xn |
|
|
kn 1 |
|
||||
|
1 |
|
|
1 |
|
|
|
1 |
|
1 |
|
||||||||||||||
|
|
|
+1 |
|
|
|
|
+1 |
< |
|
+1 |
≤ |
|
+1 |
|
|
+1 . |
||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
kn +1 |
|
|
kn +1 |
|
|
|
xn |
|
|
|
kn |
|
kn |
|
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
−1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
Теперь, поскольку |
lim |
|
|
|
|
|
|
+1 |
= lim |
|
|
+1 |
=1, а |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
kn →+∞ |
kn +1 |
|
|
|
kn →+∞ kn |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
kn +1 |
|
|
1 |
|
kn |
|
|
|
||||||||
|
|
|
|
lim |
|
|
|
|
+1 |
= lim |
|
+1 |
=e |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
kn →+∞ |
kn +1 |
|
|
kn →+∞ kn |
|
|
|
|
|
|
|||||||||||
( kn – подпоследовательность натуральных чисел, а, как известно, любая
подпоследовательность сходящейся последовательности сходится к тому же пределу, что и сама последовательность), то, с учётом (1.4.12), получа-
ем, что |
|
1 x |
|
lim 1+ |
|
=e . |
|
|
x→+∞ |
x |
|
65
Теперь рассмотрим случай x↓−∞. Для этого обозначим t =−x . Тогда
t ↑+∞. В этом случае |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 x |
|
1 −t |
t |
t |
|
1 t |
|
1 t−1 |
|
1 |
→e 1=e. |
|||||
1+ |
|
= 1− |
|
= |
|
|
|
= 1+ |
|
|
= 1+ |
|
|
1+ |
|
|
|
|
|
|
|
||||||||||||||
|
x |
|
t |
t −1 |
|
|
t −1 |
|
t −1 |
|
t −1 |
t↑+∞ |
|||||
Формулы (1.4.9) и (1.4.10) доказаны. Эти формулы и принято называть вторым замечательным пределом.
Впоследствии мы увидим, насколько важны для теории и приложений математического анализа эти два предела. Поэтому прилагательное «замечательный» было дано этим пределам не случайно.
|
Вопросы для самопроверки. |
|
|
||||||
10. Напомним, что |
f (x) , определённая на D( f ) , называется ограни- |
||||||||
ченной сверху, если |
c R x D( f ): f (x) ≤c . |
|
|
||||||
|
|
|
|
||||||
Записать условия: «f неограничена сверху», «f неограничена снизу». |
|
||||||||
20. Пусть lim f (x) =+∞. Будет ли |
f неограниченной сверху в окре- |
||||||||
x→x0 |
|
|
|
|
|
|
|
|
|
стности точки x0 ? |
|
|
|
|
|
|
|
|
|
30. Пусть в любой проколотой окрестности точки x0 |
функция |
f не- |
|||||||
ограничена сверху. Можно ли утверждать, что lim f (x) =+∞? |
|
||||||||
40. Какие свойства функции f |
|
|
x→x0 |
|
|
||||
определяют нижеследующие утвер- |
|||||||||
ждения: |
|
~ |
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
а) Uε (c) Uδ (x0 ) |
x Uδ (x0 )ID( f ): f (x) Uε (c) ; |
|
|
||||||
~ |
~ |
(x0 )ID( f ): f (x) Uε (c) ; |
|
|
|||||
б) Uε (c) U |
δ (x0 ) |
x Uδ |
|
|
|||||
~ |
|
~ |
|
|
|
|
|
|
|
в) Uε (c) U |
(x0 ) x Uδ (x0 )ID( f ): f (x) Uε (c) . |
|
|
||||||
50. Пусть ϕ(x) →+∞. Можно ли утверждать, что |
|
|
|||||||
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
ϕ( x) |
|
|
|
|
lim 1+ |
|
|
|
=e ? |
|
|
|
|
|
|
|
|
|
||||
|
|
x→x0 |
|
ϕ(x) |
|
|
|
||
60. Пусть α(x) ↓ 0 . Можно ли утверждать, что |
|
|
|||||||
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
lim (1+α(x))1/α( x) =e ? |
|
|
|||||
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
Ответы. |
|
|
||||
2. Да. 3. Нет. 4. а) существует проколотая окрестность точки |
x0 , в |
||||||||
которой f ограничена; |
б) f |
ограничена на множестве |
D( f )\{x0 }; в) |
||||||
f (x) ≡c всюду на множестве D( f )\{x0 }. 5. Да. 6. Нет. |
|
|
|||||||
66
Упражнение 1.4.
1. Найти пределы рациональных выражений:
5x + 2 а) limx →4 2x +3 .
Решение. Так как x → 4 , то числитель дроби стремится к числу 5 4 + 2 = 22 , а знаменатель – к числу 2 4 +3 =11. Следовательно,
lim |
5x + 2 |
= |
|
22 |
= 2 . |
||||||
x →4 |
2x + 3 |
|
|
11 |
|
|
|
||||
б) lim |
|
|
x2 − 2 |
|
|
; |
|||||
3x |
2 |
−5x +1 |
|||||||||
x →0 |
|
|
|||||||||
в) lim |
x2 + 3 |
; |
|
|
|
||||||
x |
2 |
−3 |
|
|
|
||||||
x →3 |
|
|
|
|
|
||||||
г) lim |
|
3x + 5 |
. |
|
|
|
|||||
|
|
|
|
|
|||||||
x |
→∞ |
2x + 7 |
|
|
|
|
|||||
Решение. Числитель и знаменатель дроби неограниченно возрастают
∞
при x → ∞, т.е имеем неопределённость вида ∞ . Разделив числитель и знаменатель дроби на x, получаем
|
|
|
|
5 |
|
|
|
|
||
|
3x + 5 |
|
3 |
+ |
|
|
|
|
3 |
|
lim |
= lim |
|
x |
|
= |
|||||
|
|
7 |
|
2 . |
||||||
x →∞ 2x + 7 |
x →∞ |
|
|
|
||||||
|
|
|
2 |
+ |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||
д) |
lim |
|
|
|
|
|
x4 −5x |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
−3x |
+ |
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x →∞ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|||||
е) |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
; |
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
lim |
2x |
−1 |
|
2x + |
|
|
|
|
|
|
|||||||||||||||||||
|
x →∞ |
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
3x |
2 |
|
|
|
|
(2x −1)(3x |
2 |
+ x + 2) |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
||||||||||||||||
ж) |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
; |
||||
|
|
2x +1 |
|
|
|
|
|
|
|
|
4x |
|
|||||||||||||||||
|
x →∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
(x +1) |
5 |
|
+ (x + 2) |
5 |
+... |
+ (x + n) |
5 |
||||||||||||||||||||
з) |
|
|
|
|
|
|
|||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
5 |
+ n |
5 |
|
|
, n N; |
|||||||
|
x →∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
и) |
lim |
|
|
x2 −9 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
− |
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x →3 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Здесь числитель и знаменатель дроби стремятся к нулю
при |
x →3 (неопределённость вида 0 ). Имеем |
|
||||||||
|
|
|
|
|
|
0 |
|
|
|
|
lim |
x2 −9 |
= lim |
(x −3)(x +3) |
= lim |
x +3 |
= |
3 +3 |
= 2 . |
||
x |
2 |
−3x |
x(x −3) |
x |
3 |
|||||
x →3 |
|
x →3 |
x →3 |
|
|
|||||
67
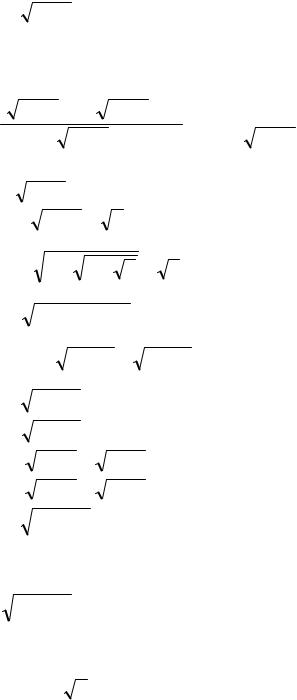
к) lim |
x2 |
− |
2x +1 |
; |
|
||
|
x |
3 |
− x |
|
|
||
x →1 |
|
|
|
|
|||
л) lim |
(x |
+ h)3 − x3 |
; |
||||
|
|
|
h |
|
|||
h →0 |
|
|
|
|
|
||
м) |
lim |
8x3 −1 |
|
; |
|||
6x |
2 |
− |
5x +1 |
||||
|
x →1/ 2 |
|
|
||||
|
|
|
x + 2 |
|
|
|
x − 4 |
|
|
|
н) |
lim |
|
|
+ |
|
|
|
|
||
|
2 |
|
|
2 |
|
|
||||
|
−5x + 4 3(x |
−3x |
+ 2) |
. |
||||||
|
x →1 x |
|
|
|
||||||
2. Найти пределы иррациональных выражений:
а) lim |
x + 4 − 2 |
. |
|
||
x →0 |
x |
|
Решение. Умножим числитель и знаменатель на сопряжённый множитель
lim |
( x + 4 − 2)( |
|
x + 4 + 2)= lim |
x + 4 − 4 |
|
= |
||||||||||||
|
|
|
|
|
|
|
x x + 4 + |
2 |
||||||||||
x →0 |
|
x( x + 4 + 2) |
|
|
x →0 |
|
||||||||||||
= lim |
|
|
|
|
1 |
|
|
= |
1 . |
|
|
|
|
|
|
|||
|
|
|
x + 4 + 2 |
|
|
|
|
|
|
|||||||||
|
x →0 |
|
4 |
|
|
|
|
|
|
|||||||||
б) |
lim |
( |
x − a − |
|
x ); |
|
|
|
|
|
|
|||||||
|
x →+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
в) |
lim |
|
x + |
x |
+ |
|
x − |
|
; |
|
|
|
||||||
|
|
x |
|
|
|
|||||||||||||
|
x →+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
г) |
lim( |
|
4x2 −7x + 4 − 2x); |
|
|
|
|
|||||||||||
|
x →∞ |
|
|
|
|
|
|
|
x3 − 2 ); |
|
|
|
||||||
д) |
lim x3/ 2 ( |
x3 + 2 − |
|
|
|
|||||||||||||
|
x →∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
е) |
lim |
|
|
x2 + 4 − 2 |
; |
|
|
|
|
|
|
|||||||
|
|
x2 + 9 − |
3 |
|
|
|
|
|
|
|||||||||
|
x →0 |
|
|
|
|
|
|
|
|
|
||||||||
ж) lim |
|
2 + x − |
2 − x |
; |
|
|
|
|
|
|||||||||
3 2 + x −3 2 − x |
|
|
|
|
|
|||||||||||||
|
x →0 |
|
|
|
|
|
|
|||||||||||
|
5 |
(1 + x)3 −1 |
|
|
|
|
|
|
||||||||||
з) |
lim |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||
|
|
x |
|
|
|
|
|
|
|
|
||||||||
|
x →0 |
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Положим 1 + x = y5 , тогда y →1 при x → 0 . Значит,
5 (1 |
+ x)3 −1 |
= lim |
y3 −1 |
= lim |
|
|
y2 + y +1 |
= |
3 |
|
||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
x |
|
|
y |
5 |
−1 |
y |
4 |
+ y |
3 |
+ y |
2 |
+ y +1 |
5 |
|||||||
x →0 |
|
|
y →1 |
|
y →1 |
|
|
|
|
|
||||||||||||
и) lim |
|
3x +1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x →∞ 5x + 3 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
68

к) |
lim |
|
x2 |
− x |
|
; |
|
|
|
|
|
x −1 |
|
||||
|
x →1 |
|
|
|
|
|||
|
|
|
|
|
|
|
||
л) |
lim |
|
|
x −1 −3 |
. |
|||
|
|
|
||||||
|
x →10 |
|
|
x −10 |
|
|
||
3. Вычислить пределы, используя первый замечательный предел:
а) lim sin mx .
x →0 x
Решение. |
lim sin mx = lim m sin mx |
= m lim sin mx |
= m . |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x →0 |
|
|
|
x |
|
|
|
x →0 |
mx |
x →0 |
mx |
|
|
|
||||
б) |
lim |
|
1 − cos 5x |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. |
lim |
1 − cos 5x |
= lim |
2 sin2 (5x / 2) |
|
sin(5x / 2) |
2 |
||||||||||||||||||||
|
|
|
x |
2 |
|
|
x |
2 |
= 2 lim |
x |
|
= |
|||||||||||||||
|
|
|
|
|
|
|
|
|
x →0 |
|
|
|
|
|
|
x →0 |
|
|
x →0 |
|
|
||||||
|
|
5 |
|
2 |
= |
|
25 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= 2 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
в) |
lim x ctgπx ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) |
lim 3arcsin x ; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x →0 |
|
|
|
|
|
4x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
д) |
lim |
|
|
|
|
|
|
|
−ctg x |
; |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x →0 sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
е) |
lim |
|
|
2 − 2 cos x |
; |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
π − 4x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x →π |
/ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ж) |
lim |
|
π |
− x |
|
|
|
|
; |
|
|
|
|
|
|
|
|
||||||||||
|
2 |
tg x |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x →π / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
з) |
lim |
|
1 + cos 5x |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x →π |
1 − cos 4x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4. Вычислить пределы, используя второй замечательный предел:
|
|
2 |
+ 5x + 4 |
x |
|
а) |
|
x |
|
|
|
|
2 |
|
|||
lim |
−3x + 7 |
. |
|||
|
x →∞ x |
|
|
||
Решение. Делением числителя дроби на знаменатель выделим целую часть:
x2 +5x + 4 |
=1 + |
|
|
8x −3 |
. |
||
x |
2 |
−3x + 7 |
x |
2 |
−3x + 7 |
||
|
|
|
|
||||
69
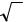
Таким образом, при x → ∞ данная функция представляет собой степень, основание которой стремится к единице, а показатель – к
бесконечности (неопределённость вида 1∞ ). Преобразуя функцию так, чтобы использовать второй замечательный предел, получим
|
|
|
2 |
+ |
5x + |
4 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
8x −3 |
|
x |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim 1 + |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
lim |
|
− |
3x + |
7 |
|
|
|
x |
−3x |
+ 7 |
|
|
|
|||||||||||||||||||||||||||||||||
x →∞ x |
|
|
|
|
|
|
|
|
x →∞ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 −3x+7 |
|
x(8 x−3) |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8x −3 |
|
|
|
x2 −3x+7 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8x−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
lim 1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|||||||||||||
|
x2 −3x + 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
x →∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 −3x+7 |
|
8−3 / x |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8x −3 |
|
|
|
|
1−3/ x+7 / x2 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8x−3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
= lim |
|
|
|
1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x2 |
−3x + |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
x →∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как |
|
|
|
8x −3 |
|
|
|
→ 0 |
|
при x →∞, то |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
− 3x + 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
8x −3 |
|
|
|
|
x2 −3x+7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
+ |
|
|
|
|
|
|
|
|
8 x−3 |
= e . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
lim 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x |
2 |
|
−3x + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
x →∞ |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 −3 / x |
|
|
|
|||||||||||||||||||
Учитывая, |
|
|
|
|
|
|
|
|
что |
|
|
|
|
|
|
|
lim |
|
|
|
= 8 , |
находим |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x →∞ x −3 / x + 7 / x |
|
|
|
|||||||||||
|
|
|
2 |
+ |
5x + |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x |
|
|
|
|
|
= e |
8 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
lim |
|
− |
3x + |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x →∞ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
x + |
3 |
2 x+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
б) |
lim |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x →∞ x − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
+ |
5 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
в) |
|
|
|
x |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
lim |
|
|
− |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x →∞ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
г) |
lim(cos x)1/ x2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x )3 / x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
д) |
lim(1 + tg2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
е) |
lim x(ln(2 + x) − ln x); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
x →∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ж) lim |
|
loga x −1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
x − a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x →a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
з) |
lim |
|
eax |
|
−ebx |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
70
