Zabotin_Dulliev_Chernyaev_-_Mat_an

Решение. Для того чтобы доказать, что последовательность {xn } имеет своим пределом число a, нужно показать, что для каждого положительного числа ε можно подобрать такое число nε (не обязательно натуральное), что при n > nε , n N будет справедливо неравенство | xn −a |< ε. Часто бывает возможно указать явную формулу, выражающую nε через ε.

можно взять 1/ ε . В самом деле, при n >1/ ε выполняется неравенство | xn |= 1 / n < ε .

5. Для каждой из последовательностей укажите все предельные точки, а также верхний и нижний пределы:

Решение. б) Точки 1 и –1, очевидно, являются предельными для последовательности xn = (−1)n . Для любой другой точки a можно по-

строить такой отрезок с центром в этой точке, в котором вообще нет ни одного члена последовательности. Поэтому других предельных

точек последовательность не имеет, а значит lim xn = −1 и

n

lim xn = 1 .

n

52

имеет; в) имеет; г) не имеет; д) имеет; е) не имеет; ж) имеет; з) не имеет. 5.

54

1.4. Пределы функций.

Начнём с определения предела функции f в бесконечноудалённой

точке, поскольку здесь будет очевидным обобщение понятия предела последовательности.

Определение 1.4.1 (по Коши). Пусть функция f определена на

(a; +∞) . Число с называется пределом функции f в точке +∞ (иногда го-

или, если обозначить Uδ (+∞) =(δ; +∞) ,

Uε (c) Uδ (+∞) x Uδ (+∞) : f (x) −c <ε.

Эквивалентность этих записей очевидна.

Для обозначения того, что число с является пределом функции f в точке +∞, применяют следующие записи:

или, если из контекста ясно, о чём идёт речь:

c =lim f (x) или f (x)→c .

Ещё одно определение числа c = lim f (x) :

x→+∞

Определение 1.4.2 (по Гейне). Пусть функция f определена на множестве (a; +∞) . Число c R называется пределом функции f при х

Обозначение предела, приведённое выше, сохраняется и в этом случае, поскольку, как мы увидим, определения Коши и Гейне эквивалентны.

Эти определения описывают свойство графика функции: приближение к некоторому уровню с при неограниченном движении наблюдателя

55

вдоль графика функции вправо. Важно понимать, что при этом х никуда не стремится и запись x→+∞ носит чисто символический характер, поскольку формально определить эту запись невозможно.

В качестве упражнения запишите «на языках Коши и Гейне» опреде-

ление: c = lim f (x) .

x→−∞

Не меньший интерес представляет свойство значений функции приближаться (или не приближаться) к числу с, если значения аргумента будут выбираться всё ближе и ближе к некоторому числу x0 . В этом случае аналогия с последовательностью частично пропадает, поскольку значения аргумента х уже не увеличиваются бесконечно.

Для точных определений предела функции в точке нам понадобится следующее понятие:

Определение 1.4.3. Пусть A R . Точка x0 R называется предель-

~

ной точкой множества А, если A IU δ (x0 ) ≠, какова бы ни была проколо-

~

тая окрестность Uδ (x0 ) .

Иными словами, x0 – предельная точка множества А, если в любой её окрестности есть точки из А, отличные от x0 .

Очевидно, что любая точка отрезка [a, b ] является предельной точкой интервала (a, b ). Так же очевидно, что точка x0 =0 является предельной точкой множества {xn =1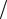n; n N }.

Более сложный пример: пусть А – множество всех рациональных точек отрезка [0;1], тогда сам отрезок [0;1] будет множеством предельных

точек множества А. Действительно: какова бы ни была точка x [0;1] , в любой её проколотой окрестности найдётся рациональная точка из [0;1] независимо от того, будет ли х рациональной или иррациональной точкой.

Определение предела функции в точке по Коши.

ε>0 δ>0 x D( f ): (0< x −x0 <δ f (x) −c <ε).

Следует обратить особое внимание на то, что x0 в этом определении не обязана принадлежать множеству D( f ) ! Иными словами, нас не интересует, как определена f в точке x0 и определена ли в ней вообще.

56

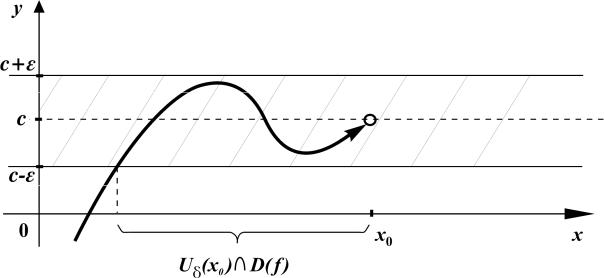
Геометрическое истолкование этого определения следующее: какую бы полосу {(x, y): x R, c −ε< y <c +ε} на числовой плоскости мы бы ни

~

взяли, найдётся Uδ (x0 ) такая, что точки

{ ~ = }

(x, y): x Uδ (x0 )ID( f ), y f (x)

будут лежать в этой полосе:

пределах в точке x0 .

В этом случае очевидным является следующее утверждение.

Теорема 1.4.1 (о связи предела функции с её односторонними пределами).

Если f определена хотя бы в проколотой окрестности точки x0 , то

число c =lim f (x) тогда и только тогда, когда

x→x0

57

c =lim f (x) =lim f (x) .

x↑x0 x↓x0

Доказательство провести самостоятельно.

Определение предела функции в точке по Гейне.

Пусть x0 – предельная точка D( f ) . Число с назовём пределом функции в точке x0 , если какова бы ни была последовательность xn со значениями в D( f ) , такая, что n : xn ≠ x0 , будет выполняться:

Обозначения предела функции остаются теми же, что и в определении Коши. Очевидным образом определяются односторонние пределы, для

этого в (1.4.4) нужно предполагать xn ↓x0 или xn ↑x0 для введения право-

стороннего и левостороннего пределов соответственно.

Остаётся в силе и теорема о связи односторонних пределов с пределом функции.

Разумеется, что два разных определения одного и того же объекта не должны противоречить друг другу, иначе мы получили бы две «разных математики». Поэтому докажем следующую теорему:

Теорема 1.4.2 (об эквивалентности определений предела по Коши и Гейне).

Число с является пределом f в точке x0 по Коши тогда и только тогда, когда оно является пределом f в точке x0 по Гейне.

Доказательство. Пусть с удовлетворяет условию (1.4.3). Зададим произвольное число ε>0 и возьмём произвольную последовательность

xn ≠ x0 со значениями в D( f ) и такую, что xn →n x0 . Тогда

~

nδ n >nδ : xn Uδ (x0 )ID( f ) ,

~

где Uδ (x0 ) – окрестность, фигурирующая в условии (1.4.3). Но тогда из (1.4.3) последует:

выполняется.

Теорема доказана.

Упражнение. Доказать, что определения Коши и Гейне пределов f в бесконечноудалённой точке эквивалентны.

58

Доказанная теорема позволяет нам применять любое из данных определений в тех случаях, когда одно из них облегчает рассуждения, связанные с доказательствами того или иного результата, и мы будем этим широко пользоваться.

Так, для того чтобы доказать, что в точке x0 функция не обладает пределом, достаточно найти две разных последовательности, сходящихся к x0 , на которых значения функции сходятся к двум различным пределам.

Например, покажем, что функция f (x) =sin 1x , определённая всюду,

кроме точки x0 =0 , не имеет предела при x→0 . Для этого рассмотрим

Упражнение. Также с помощью определения Гейне доказать, что функция Дирихле

0, x−рационально, f (x) =

1, x−иррационально

не имеет предела ни в какой точке x0 R . (Можно, например, рассмотреть xn →n x0 и yn →n x0 , но значения xn состоят из рациональных чисел, а значения yn – из иррациональных.)

Очень часто при анализе функций возникает вопрос: как доказать,

что существует lim f (x) , если заранее не задано число с, фигурирующее в

x→x0

условиях (1.4.3) или (1.4.4)? Этот вопрос аналогичен тому, который решался с помощью критерия Коши для числовых последовательностей. Помните, мы доказали, что xn обладает пределом тогда и только тогда, когда она фундаментальна? Конечно, это была чистая «теорема существования», не дающая ответа на вопрос: а чему равен этот предел? Но при теоретических исследованиях знания того, что предел существует, часто бывает достаточно, чтобы продолжить исследования.

Лемма 1.4.3. Пусть для любой последовательности xn , сходящейся к x0 , последовательность f (xn ) имеет предел. Тогда f (x) имеет предел в

точке x0 .

Доказательство проведём по Гейне. Пусть xn →n x0 , yn →n y0 – две произвольных последовательности со значениями в D( f ) . Построим тре-

тью последовательность:

t1 =x1 , t2 = y1 , t3 =x2 , t4 = y2 , ... , t2n−1 =xn , t2n = yn , ...

59

Очевидно tn →n x0 , но тогда по условию леммы существует число

казали, что число с удовлетворяет определению предела по Гейне.

Теорема 1.4.4 (критерий Коши). Для того чтобы существовал предел f в точке x0 , необходимо и достаточно выполнения следующего усло-

вия:

Возьмём ε>0 и построим, по определению Коши, соответствующую

Поскольку 2ε – вновь произвольное положительное число, мы доказали, что выполняется условие (1.4.4).

Достаточность. Здесь удобнее воспользоваться определением Гейне. Пусть xn →n x0 – последовательность со значениями в D( f ) , а условие

(1.4.4) выполняется. Тогда в силу сходимости xn

δ>0 nδ n, m>nδ : f (xn ) − f (xm ) <ε,

т. е. f (xn ) фундаментальна, а значит, имеет предел. Учитывая произвольность выбора xn и предыдущую лемму, получаем доказательство доста-

той окрестности x0 . Все нижеследующие свойства будут, очевидно, справедливы и для односторонних пределов, и для пределов в бесконечно удалённых точках.

Теорема 1.4.5. Функция, имеющая конечный предел в точке x0 , ограничена в некоторой окрестности этой точки.

60