а) |
б) |
Рис.6.6.
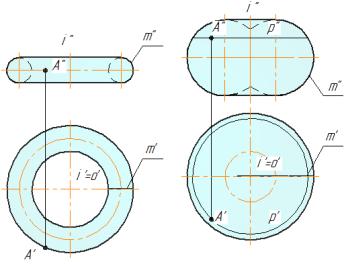
6.5. Порядок поверхности.
1.Порядок поверхности в начертательной геометрии определяется максимальным количеством точек (действительных или мнимых), в которых прямая пересекает данную поверхность.
Примеры.
Плоскость - поверхность первого порядка, прямая может пересечь не более чем в одной точке. Сферу, круговой цилиндр - поверхности второго порядка, прямая может пересечь двух точках. Тор - поверхности четвертого порядка, прямая может пересечь не более чем четырех точках.
2. Плоскость пересекает поверхность n –го порядка по кривой того же порядка.
Примеры.
Плоскость может пересечь другую плоскость по прямой, т.е.по линии первого порядка. Сферу - поверхности второго порядка, плоскость может пересечь по окружности, т.е. кривой второго порядка . Тор - поверхности четвертого порядка, прямая может пересечь не более чем четырех точках.
55
6.6 Сечение поверхности |
проецирующей |
плоскостью. |
|
|
|
|
|
||||||||
|
Построение проекций плоской фигуры, получающейся |
в |
сечении, |
||||||||||||
производится в данном |
случае |
|
просто, так |
как |
одна |
из проекций |
совпадает |
с |
|||||||
соответствующим следом секущей плоскости, т.е. |
является |
прямой |
линией. |
|
|||||||||||
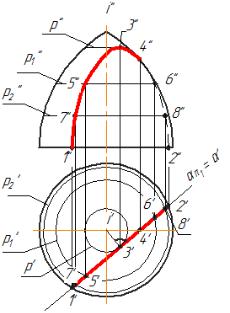
На |
рис.6.7 приведен |
пример |
сечения |
поверхности |
вращения горизонтально- |
||||||||||
проецирующей |
плоскостью |
α. В этом |
случае |
горизонтальная |
проекция сечения |
||||||||||
будет |
представлять |
собой. |
прямую |
линию, |
|
совпадающей |
с горизонтальным |
||||||||
следом плоскости α. |
Зная, что |
эта |
линия принадлежит поверхности, можно легко |
||||||||||||
построить ее |
фронтальную проекцию. |
Построение начинаем |
с |
точек |
1 |
и |
2, |
||||||||
принадлежащих окружности основания. Построение точек 3,4 является типичным для построения промежуточных точек. Построение точки 5 иллюстрирует определение верхней точки сечения. Точка 6 - точка сечения, принадлежащая главному меридиану, в которой на фронтальной проекции кривая фигуры сечения из видимой переходит в невидимую.
Переход видимой ветви кривой сечения в невидимую, всегда происходит в точке, лежащей на очерке поверхности.
Рис. 6.7
6.7 Конические сечения.
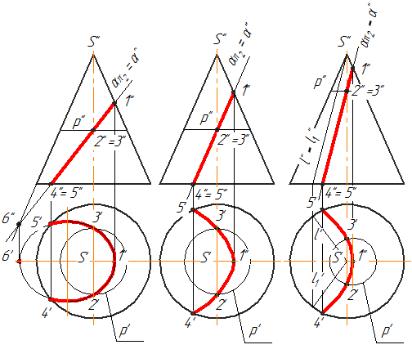
Круговой цилиндр можно рассечь по эллипсу и по прямым линиям. Эллипс получится в том случае, если секущая плоскость будет наклонной по отношению к оси цилиндра. Если же секущая плоскость будет параллельна оси цилиндра она рассечет последний по прямым линиям - его образующим.
а |
б |
в |
|
|
Рис. 6.8 |
Более разнообразны сечения кругового конуса. Прежде всего надо отметить тот единственный случай, когда конус пересекается плоскостью по двум прямым – образующим. Это может иметь место лишь при условии, если секущая плоскость проходит через вершину конуса.
Если же секущая плоскость не проходит через вершину конуса, то в сечении получаются кривые линии, причём они могут быть только трёх видов: эллипсы, параболы и гиперболы. Все эти кривые, как известно, являются кривыми второго порядка.
Эллипс получается в сечении конуса наклонной плоскостью, не параллельной ни одной из его образующих, т.е. пересекающей все образующие конуса (или их продолжения) (рис. 6.8 а).
Парабола получается в том случае, если секущая плоскость параллельна какойлибо одной образующей (рис.6.8 б)
Гипербола получается при условии, если секущая плоскость параллельна двум образующим. В частности, это будет иметь место тогда, когда секущая плоскость параллельна оси конуса (рис.6.8 в).
Ясно, что в обоих последних случаях кривая сечения должна быть разомкнутой, так как плоскость пересекает не все образующие.
57
6.8 Пересечение прямой с поверхностью. Алгоритм определения точек пересечения прямой с поверхностью.
Рассмотрим общий случай. Под общим будем понимать случай, при котором прямая занимает общее положение, как относительно плоскостей проекций, так и относительно поверхности.
Алгоритм решения задачи на отыскание точек пересечения прямой с поверхностью по своей сути ничем не отличается от алгоритма решения задачи на
отыскание точки пересечения прямой с плоскостью.
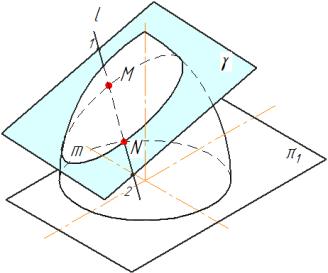
Рис. 6.9
Алгоритм задачи на пересечение прямой с поверхностью (рис.6.9) состоит в следующем.
Для того, чтобы отыскать точки пересечения прямой с поверхностью (α) необходимо:
1.заключить прямую во вспомогательную секущую плоскость,
ℓγ,
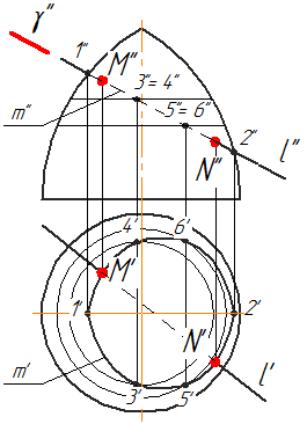
2.построить фигуру сечения поверхности данной плоскостью,
m= α∩γ,
3.построить точки пересечения прямой с поверхностью, как точки пересечения прямой с найденной линией сечения.
(М , N)= ℓ ∩ α= ℓ ∩m,
4.выделить видимые и невидимые участки прямой.
Настоящая задача является более сложной, чем задача на определение точки пересечения прямой с плоскостью. Это усложнение состоит в том, что если в первой задаче фигурой сечения была прямая, то в настоящей задаче фигурой сечения, как правило, будет кривая линия. Необходимо выбрать положение секущей плоскости так, чтобы фигура сечения оказалась простейшей, что в свою очередь, приведёт к упрощению решения задачи.
Рассмотрим решение типовой задачи на комплексном чертеже. Необходимо найти точки пресечения прямой ℓ с поверхностью вращения.
Рис. 6.10
На рис.6.10 через прямую ℓ проведена фронтально-проецирующая плоскость γ (прямая ℓ заключена в плоскость γ). Линия сечения m строится так, как
59